ষষ্ঠ/ ৬ষ্ঠ শ্রেণির গণিত সমাধান অনুশীলনী ১.৩ পোস্টে সকলকে স্বাগতম। এখানে ষষ্ঠ শ্রেণির গণিত বিষয়ের সকল অধ্যায়ের সমাধান দেওয়া হয়েছে। প্রথম অধ্যায় স্বাভাবিক সংখ্যা ও ভগ্নাংশ এর অন্যান্য অনুশীলনীগুলোর সমাধান দেখতে পোস্টের নিচে চোখ রাখুন।

৬ষ্ঠ শ্রেণির গণিত সমাধান অনুশীলনী ১.৩

প্রশ্ন- ১ মৌলিক গুণনীয়কের সাহায্যে গ.সা.গু. নির্ণয় কর :
(ক) ১৪৪, ২৪০ ও ৬১২
সমাধান : ১৪৪, ২৪০ ও ৬১২ কে মৌলিক গুণনীয়কে বিশ্লেষণ করে পাই,
২ |১৪৪          ২ |২৪০           ২ |৬১২
   ২ |৭২            ২ |১২০           ২ |৩০৬
      ২ |৩৬          ২ |৬০            ৩ |১৫৩
        ২ |১৮            ২ |৩০            ৩ |৫১
          ৩ |৯               ৩ |১৫               ১৭
               ৩                     ৫
এখানে,
১৪৪ এর গুণনীয়কগুলো ২, ২, ২, ২, ৩, ৩
২৪০ এর গুণনীয়কগুলো ২, ২, ২, ২, ৩, ৫
৬১২ এর গুণনীয়কগুলো ২, ২, ৩, ৩, ১৭
১৪৪, ২৪০ এবং ৬১২ এর সাধারণ মৌলিক গুণনীয়কগুলো হলো : ২, ২, ৩
∴ ১৪৪, ২৪০ এবং ৬১২ এর গ.সা.গু= ২ × ২ × ৩ = ১২
উত্তর : গ.সা.গু ১২।

(খ) ৫২৫, ৪৯৫ ও ৫৭০
সমাধান : ৫২৫, ৪৯৫ ও ৫৭০ কে মৌলিক গুণনীয়কে বিশ্লেষণ করে পাই,
 ৩ |৫২৫         ৩ |৪৯৫          ২ |৫৭০
    ৫ |১৭৫        ৩ |১৬৫           ৩ |২৮৫
       ৫ |৩৫         ৫ |৫৫             ৫ |৯৫
              ৭                    ১১                    ১৯
এখানে,
৫২৫ এর মৌলিক গুণনীয়কগুলো ৩, ৫, ৫, ৭
৪৯৫ এর মৌলিক গুণনীয়কগুলো ৩, ৩, ৫, ১১
৫৭০ এর মৌলিক গুণনীয়কগুলো ২, ৩, ৫, ১৯
৫২৫, ৪৯৫ এবং ৫৭০ এর সাধারণ মৌলিক গুণনীয়কগুলো ৩, ৫।
∴ ৫২৫, ৪৯৫ এবং ৫৭০ এর গ.সা.গু. = ৩ × ৫ = ১৫
উত্তর : গ.সা.গু ১৫।

(গ) ২৬৬৬, ৯৬৯৯
সমাধান : ২৬৬৬, ৯৬৯৯ কে মৌলিক গুণনীয়কে বিশ্লেষণ করে পাই,
২ |২৬৬৬              ৩ |৯৬৯৯
   ৩১ |১৩৩৩          ৫৩|৩২৩৩
            ৪৩                         ৬১
এখানে,
২৬৬৬ এর মৌলিক গুণনীয়কগুলো ২, ৩১, ৪৩
৯৬৯৯ এর মৌলিক গুণনীয়কগুলো ৩, ৫৩, ৬১
∴ ২৬৬৬ এবং ৯৬৯৯ এর মধ্যে কোনো সাধারণ মৌলিক গুণনীয়ক নেই।
উত্তর : গ.সা.গু. ১।

প্রশ্ন- ২ ভাগ প্রক্রিয়ায় গ.সা.গু. নির্ণয় কর :
(ক) ১০৫, ১৬৫
সমাধান :

১০৫ ) ১৬৫ (১
            ১০৫
           ৬০ ) ১০৫ (১
                      ৬০
                      ৪৫ ) ৬০ (১
                                ৪৫
                                ১৫ ) ৪৫ (৩
                                         ৪৫
                                           ০
শেষ ভাজক ১৫।
∴ ১০৫ ও ১৬৫ এর গ.সা.গু. ১৫।
উত্তর : গ.সা.গু. ১৫।

(খ) ৩৮৫, ২৮৬, ৪১৮
সমাধান :

২৮৬ ) ৩৮৫ ( ১
             ২৮৬
                ৯৯ ) ২৮৬ ( ২
                          ১৯৮
                           ৮৮ ) ৯৯ ( ১
                                     ৮৮
                                      ১১ ) ৮৮ ( ৮
                                              ৮৮
                                                ০
আবার, ১১ ) ৪১৮ ( ৩৮
                    ৩৩
                       ৮৮
                       ৮৮
                         ০
এখানে, শেষ ভাজক ১১, যা ২৮৬ ও ৩৮৫ এর গ. সা. গু.।
∴ ২৮৬, ৩৮৫ ও ৪১৮ এর গ.সা.গু. ১১।
উত্তর : গ.সা.গু. ১১।

প্রশ্ন- ৩ মৌলিক গুণনীয়কের সাহায্যে ল.সা.গু. নির্ণয় কর :
(ক) ১৫, ২৫, ৩০
সমাধান : এখানে, ১৫ = ৩ × ৫
২৫ = ৫ × ৫
৩০ = ২ × ৩ × ৫
∴ ১৫ এর মৌলিক গুণনীয়কগুলো ৩, ৫
২৫ এর মৌলিক গুণনীয়কগুলো ৫, ৫
৩০ এর মৌলিক গুণনীয়কগুলো ২, ৩, ৫
প্রদত্ত সংখ্যাগুলোর মৌলিক গুণনীয়কে ২ আছে সর্বোচ্চ একবার, ৩ আছে সর্বোচ্চ একবার এবং ৫ সর্বাধিক দুইবার।
এখন, ২ একবার, ৩ একবার ও ৫ দুইবার নিয়ে ধারাবাহিক গুণ করলে নির্ণেয় ল. সা. গু. পাওয়া যাবে।
∴ ল.সা.গু. = ২ × ৩ × ৫ × ৫ = ১৫০
উত্তর : ল.সা.গু. ১৫০।

(খ) ২২, ৮৮, ১৩২, ১৯৮
সমাধান :
২ |২২      ২ |৮৮      ২ |১৩২      ২ |১৯৮
     ১১         ২ |৪৪       ২ |৬৬      ৩ |৯৯
                     ২ |২২      ৩ |৩৩      ৩ |৩৩
                          ১১            ১১            ১১
∴ ২২ এর মৌলিক গুণনীয়কগুলো ২, ১১
৮৮ এর মৌলিক গুণনীয়কগুলো ২, ২, ২, ১১
১৩২ এর মৌলিক গুণনীয়কগুলো ২, ২, ৩, ১১
১৯৮ এর মৌলিক গুণনীয়কগুলো ২, ৩, ৩, ১১
প্রদত্ত সংখ্যাগুলোর মৌলিক গুণনীয়কে ২ আছে সর্বাধিক তিনবার, ৩ আছে সর্বাধিক দুইবার এবং ১১ আছে একবার। এখন, ২ তিনবার, ৩ দুইবার ও ১১ একবার নিয়ে ধারাবাহিক গুণ করলে নির্ণেয় ল.সা.গু. পাওয়া যাবে।
∴ ল.সা.গু. = ২ × ২ × ২ × ৩ × ৩ × ১১ = ৭৯২
উত্তর : ল.সা.গু. ৭৯২।

(গ) ২৪, ৩৬, ৫৪, ৭২, ৯৬
সমাধান :
২ |২৪       ২ |৩৬       ২ |৫৪
    ২ |১২      ২ |১৮        ৩ |২৭
       ২ |৬       ৩ |৯          ৩ |৯
          ৩           ৩              ৩

২ |৭২           ২ |৯৬
  ২ |৩৬           ২ |৪৮
       ২ |১৮         ২ |২৪
         ৩ |৯           ২ |১২
            ৩              ২ |৬
                                 ৩
∴ ২৪ এর মৌলিক গুণনীয়কগুলো ২, ২, ২, ৩
৩৬ ,, ,, ,, ২, ২, ৩, ৩
৫৪ ,, ,, ,, ২, ৩, ৩, ৩
৭২ ,, ,, ,, ২, ২, ২, ৩, ৩
৯৬ ,, ,, ,, ২, ২, ২, ২, ২, ৩
প্রদত্ত সংখ্যাগুলোর মৌলিক গুণনীয়কে ২ সর্বাধিক পাঁচবার এবং ৩ সর্বাধিক তিনবার। এখন, ২ পাঁচবার ও ৩ তিনবার নিয়ে ধারাবাহিক গুণ করলে নির্ণেয় ল. সা. গু. পাওয়া যাবে।
∴ ল. সা. গু. = ২ × ২ × ২ × ২ × ২ × ৩ × ৩ × ৩
= ৮৬৪
উত্তর : ল.সা.গু. ৮৬৪।

প্রশ্ন- ৪ ইউক্লিডীয় পদ্ধতিতে ল.সা.গু. নির্ণয় কর :
(ক) ৯৬, ১২০
সমাধান :
২ |৯৬, ১২০
   ২ |৪৮, ৬০
       ২ |২৪, ৩০
         ৩ |১২, ১৫
                ৪, ৫
নির্ণেয় ল.সা.গু. = ২ × ২ × ২ × ৩ × ৪ × ৫
= ৪৮০
উত্তর : ৪৮০।

(খ) ৩৫, ৪৯, ৯১
সমাধান : ৭|৩৫, ৪৯, ৯১
                      ৫, ৭, ১৩
নির্ণেয় ল.সা.গু. = ৭ × ৫ × ৭ × ১৩ = ৩১৮৫
উত্তর : ৩১৮৫

(গ) ৩৩, ৫৫, ৬০, ৮০, ৯০

নির্ণেয় ল. সা. গু. = ২ × ২ × ৩ × ৫ × ১১ × ৪ × ৩ = ৭৯২০
উত্তর : ৭৯২০

প্রশ্ন- ৫ কোন বৃহত্তম সংখ্যা দ্বারা ১০০ ও ১৮৪ কে ভাগ করলে প্রত্যেকবার ভাগশেষ ৪ থাকবে?
সমাধান : যেহেতু, বৃহত্তম সংখ্যা দ্বারা ১০০ ও ১৮৪ কে ভাগ করলে প্রত্যেকবার ভাগশেষ ৪ থাকে।
কাজেই, বৃহত্তম সংখ্যাটি হবে, (১০০ – ৪) বা ৯৬ এবং (১৮৪ – ৪) বা ১৮০ এর নির্ণেয় গ.সা.গু.।
এখন, ৯৬)১৮০(১
                   ৯৬
                   ৮৪)৯৬(১
                          ৮৪
                           ১২)৮৪(৭
                                  ৮৪
                                   ০
∴ ৯৬ ও ১৮০ এর গ.সা.গু. ১২
উত্তর : বৃহত্তম সংখ্যাটি ১২।

প্রশ্ন- ৬ কোন বৃহত্তম সংখ্যা দ্বারা ২৭, ৪০ ও ৬৫ কে ভাগ করলে যথাক্রমে ৩, ৪, ৫ ভাগশেষ থাকবে?
সমাধান : যেহেতু, বৃহত্তম সংখ্যাটি দ্বারা ২৭, ৪০ ও ৬৫ কে ভাগ করলে যথাক্রমে ৩, ৪ ও ৫ ভাগশেষ থাকে।
কাজেই বৃহত্তম সংখ্যাটি হবে, (২৭ – ৩) বা ২৪, (৪০ – ৪) বা, ৩৬ এবং (৬৫ – ৫) = ৬০ এর নির্ণেয় গ.সা.গু.।
২৪ ) ৩৬ ( ১
          ২৪
           ১২ ) ২৪ ( ২
                    ২৪
                      ০
আবার, ১২ ) ৬০ ( ৫
                      ৬০
                         ০
∴ ২৪, ৩৬, ৬০ এর গ.সা.গু. ১২।
উত্তর : বৃহত্তম সংখ্যা ১২।

প্রশ্ন- ৭ কোন ক্ষুদ্রতম সংখ্যাকে ৮, ১২, ১৮ এবং ২৪ দ্বারা ভাগ করলে প্রত্যেকবার ভাগশেষ ৫ হবে?
সমাধান : নির্ণেয় ক্ষুদ্রতম সংখ্যাকে ৮, ১২, ১৮ এবং ২৪ দিয়ে ভাগ করলে প্রত্যেকবারই ৫ ভাগশেষ থাকে।
নির্ণেয় ক্ষুদ্রতম সংখ্যাটি হবে ৮, ১২, ১৮ ও ২৪ এর ল. সা. গু. অপেক্ষা ৫ বেশি।

∴ ল.সা.গু. = ২ × ২ × ২ × ৩ × ৩ = ৭২
নির্ণেয় ক্ষুদ্রতম সংখ্যাটি (৭২ + ৫) বা ৭৭।
উত্তর : ৭৭।

প্রশ্ন- ৮ কোন ক্ষুদ্রতম সংখ্যাকে ২০, ২৫, ৩০, ৩৬ এবং ৪৮ দিয়ে ভাগ করলে যথাক্রমে ১৫, ২০, ২৫, ৩১ ও ৪৩ ভাগশেষ থাকবে?
সমাধান : এখানে, ২০ – ১৫ = ৫; ২৫ – ২০ = ৫; ৩০ – ২৫ = ৫; ৩৬ – ৩১ = ৫ এবং ৪৮ – ৪৩ = ৫
∴ প্রতিক্ষেত্রে ৫ অবশিষ্ট থাকে।
অতএব, ক্ষুদ্রতম সংখ্যাটি হবে ২০, ২৫, ৩০, ৩৬ ও ৪৮ এর ল.সা.গু. থেকে ৫ কম।

∴ ল. সা. গু. = ২ × ২ × ৩ × ৫ × ৫ × ৩ × ৪ = ৩৬০০
নির্ণেয় ক্ষুদ্রতম সংখ্যাটি (৩৬০০ – ৫) বা ৩৫৯৫।
উত্তর : ৩৫৯৫।

প্রশ্ন- ৯ একটি লোহার পাত ও একটি তামার পাতের দৈর্ঘ্য যথাক্রমে ৬৭২ সে. মি. ও ৯৬০ সে. মি.। পাত দুইটি থেকে কেটে নেওয়া একই মাপের সবচেয়ে বড় টুকরার দৈর্ঘ্য কত হবে? প্রত্যেক পাতের টুকরার সংখ্যা নির্ণয় কর।
সমাধান : এখানে, পাত দুইটি হতে কেটে নেওয়া একই মাপের সবচেয়ে বড় টুকরার দৈর্ঘ্য হবে লোহার পাত ও তামার পাতের প্রদত্ত দৈর্ঘ্যরে নির্ণেয় গ.সা.গু.।
∴ প্রক্রিয়ায় ৬৭২ সে. মি. ও ৯৬০ সে. মি. এর গ. সা. গু. নির্ণয় করি।
৬৭২)৯৬০( ১
           ৬৭২
           ২৮৮)৬৭২(২
                     ৫৭৬
                       ৯৬)২৮৮(৩
                               ২৮৮
                                  ০
∴ ৬৭২ ও ৯৬০ এর গ.সা.গু. ৯৬।
অর্থাৎ, কেটে নেয়া সবচেয়ে বড় টুকরার দৈর্ঘ্য ৯৬ সে.মি.।
∴ লোহার পাতের টুকরার সংখ্যা = ৬৭২÷৯৬ টি বা ৭টি
এবং তামার পাতের টুকরার সংখ্যা = ৯৬০÷৯৬ টি বা ১০টি
উত্তর : সবচেয়ে বড় টুকরার দৈর্ঘ্য ৯৬ সে.মি. লোহার পাত ৭ টুকরা; তামার পাত ১০ টুকরা।

প্রশ্ন- ১০ চার অঙ্কের কোন ক্ষুদ্রতম সংখ্যা ১২, ১৫, ২০ ও ৩৫ দ্বারা নিঃশেষে বিভাজ্য?
সমাধান : প্রথমে প্রদত্ত ভাজক ১২, ১৫, ২০ ও ৩৫ এর ল.সা. গু. নির্ণয় করি।

নির্ণেয় ল.সা.গু. = ২ × ২ × ৩ × ৫ × ৭ = ৪২০
আমরা জানি, চার অঙ্কের ক্ষুদ্রতম সংখ্যা ১০০০
সুতরাং ১২, ১৫, ২০ ও ৩৫ দ্বারা নিঃশেষে বিভাজ্য চার অঙ্কের ক্ষুদ্রতম সংখ্যা নির্ণয়ের জন্য, প্রথমে ৪২০ দ্বারা ১০০০ কে ভাগ করি।
৪২০ ) ১০০০ (২
           ৮৪০
            ১৬০
দেখা যাচ্ছে ১০০০ সংখ্যাটি ৪২০ দ্বারা বিভাজ্য নয়। এখানে বিভাজ্য সংখ্যাটি হবে ১০০০ হতে ১৬০ কম অথবা ১০০০ হতে (৪২০ -১৬০) বা ২৬০ বেশি। কিন্তু ১০০০ হতে ১৬০ কম হলে সংখ্যাটি তিন অঙ্কের বিধায় গ্রহণ যোগ্য নয়।
সুতরাং সংখ্যাটি হবে (১০০০ + ২৬০) বা ১২৬০
উত্তর : চার অঙ্কের ক্ষুদ্রতম সংখ্যাটি ১২৬০।

প্রশ্ন- ১১ পাঁচ অঙ্কের কোন বৃহত্তম সংখ্যাকে ১৬, ২৪, ৩০ ও ৩৬ দিয়ে ভাগ করলে প্রত্যেকবার ভাগশেষ ১০ হবে?
সমাধান :

∴ ল.সা.গু. = ২ × ২ × ২ × ৩ × ২ × ৫ × ৩ = ৭২০
আমরা জানি, পাঁচ অঙ্কের বৃহত্তম সংখ্যা ৯৯৯৯৯।
সুতরাং ৯৯৯৯৯ কে ৭২০ দ্বারা ভাগ করে নিঃশেষে বিভাজ্য সংখ্যা নির্ণয় করি।
৭২০ ) ৯৯৯৯৯ ( ১৩৮
           ৭২০
             ২৭৯৯
             ২১৬০
               ৬৩৯৯
               ৫৭৬০
                  ৬৩৯
৯৯৯৯৯ সংখ্যাটি ৭২০ দ্বারা বিভাজ্য নয়। এখানে ৬৩৯ অবশিষ্ট থাকে। ভাজ্য ৯৯৯৯৯ থেকে ৬৩৯ কম হলে প্রাপ্ত সংখ্যাটি ৭২০ দ্বারা বিভাজ্য হবে।
আবার, (৭২০ – ৬৩৯) বা ৮১ বেশি হলেও ৭২০ দ্বারা বিভাজ্য হবে। কিন্তু (৯৯৯৯৯ + ৮১) বা ১০০০৮১ সংখ্যাটি ৬ অঙ্কবিশিষ্ট। যা গ্রহণযোগ্য নয়।
কাজেই নিঃশেষে বিভাজ্য পাঁচ অঙ্কের বৃহত্তম সংখ্যা হবে
(৯৯৯৯৯ – ৬৩৯) বা ৯৯৩৬০।
প্রশ্নমতে, প্রত্যেকবার ভাগশেষ ১০ বিদ্যমান থাকে।
∴ বৃহত্তম সংখ্যাটি (৯৯৩৬০ + ১০) বা ৯৯৩৭০
উত্তর : বৃহত্তম সংখ্যা ৯৯৩৭০।

প্রশ্ন- ১২ কোনো বাসস্ট্যান্ড থেকে ৪টি বাস একটি নির্দিষ্ট সময় পর যথাক্রমে ১০ কি.মি.,২০ কি.মি., ২৪ কি.মি. ও ৩২ কি.মি. পথ অতিক্রম করে। কমপক্ষে কতদূর পথ অতিক্রম করার পর বাস চারটি একত্রে মিলিত হবে?
সমাধান : এখানে নির্ণেয় ন্যূনতম দূরত্ব হবে ১০, ২০, ২৪ ও ৩২ কিলোমিটারের ল.সা.গু.।

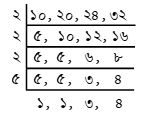
∴ ল.সা.গু. = ২ × ২ × ২ × ৫ × ৩ × ৪ = ৪৮০
উত্তর : ৪৮০ কি. মি. দূরত্ব অতিক্রম করার পর বাস চারটি একত্রে মিলিত হবে।

প্রশ্ন- ১৩ দুইটির সংখ্যার গুণফল ৩৩৮০ এবং গ.সা.গু. ১৩। সংখ্যা দুইটির ল.সা.গু. নির্ণয় কর।
সমাধান : আমরা জানি,
দুইটি সংখ্যার গুণফল = সংখ্যাদ্বয়ের গ.সা.গু. × সংখ্যাদ্বয়ের ল.সা.গু.
প্রশ্নমতে, সংখ্যা দুইটির গুণফল = ৩৩৮০
এবং গ.সা.গু. = ১৩
∴ ১৩ × ল.সা.গু. = ৩৩৮০
∴ ল.সা.গু. = ৩৩৮০÷১৩ = ২৬০
উত্তর : সংখ্যা দুইটির ল.সা.গু. ২৬০।

🔶🔶 ৬ষ্ঠ শ্রেণির গণিত সমাধান

🔶🔶 ৬ষ্ঠ শ্রেণির সকল বিষয় সমাধান