এসএসসি সাধারণ গণিত নবম অধ্যায় ত্রিকোণমিতিক অনুপাত ৯.২ অনুশীলনীর প্রশ্ন ও সমাধান

নবম-দশম শ্রেণির বা এসএসসি সাধারণ গণিত নবম অধ্যায় ত্রিকোণমিতিক অনুপাত ৯.২ অনুশীলনীর প্রশ্ন ও সমাধান সহ সকল অধ্যায়ের অনুশীলনীর প্রশ্ন উত্তর সহ MCQ ও সৃজনশীল প্রশ্ন ব্যাংক পেতে সম্পূর্ণ পোস্টটি পড়ুন।

অধ্যায় ৯ ত্রিকোণমিতিক অনুপাত ৯.২ অনুশীলনী

পাঠ সম্পর্কিত গুরুত্বপূর্ণ বিষয়াদি

বিভিন্ন কোণের ত্রিকোণমিতিক অনুপাতের মান

কোণ অনুপাত	0°	30°	45°	60°	90°
sine	0	$\frac{1}{2}$	$\frac{1}{{\sqrt 2 }}$	$\frac{{\sqrt 3 }}{2}$	1
cosine	1	$\frac{{\sqrt 3 }}{2}$	$\frac{1}{{\sqrt 2 }}$	$\frac{1}{2}$	0
tangent	0	$\frac{1}{{\sqrt 3 }}$	1	$\sqrt 3$	অসংজ্ঞায়িত
cotangent	অসংজ্ঞায়িত	$\sqrt 3$	1	$\frac{1}{{\sqrt 3 }}$	0
secant	1	$\frac{2}{{\sqrt 3 }}$	$\sqrt 2$	2	অসংজ্ঞায়িত
cosecant	অসংজ্ঞায়িত	2	$\sqrt 2$	$\frac{2}{{\sqrt 3 }}$	1

নবম-দশম শ্রেণির ৯.২ অনুশীলনীর প্রশ্ন ও সমাধান

প্রশ্ন \ 1 \ cosθ = $\frac{{\bf{1}}}{{\bf{2}}}$ হলে, cotθ এর মান কোনটি?
√ $\frac{1}{{\sqrt 3 }}$ (খ) 1 (গ) 3 (ঘ) 2
ব্যাখ্যা :

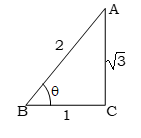
নবম-দশম শ্রেণির ৯.২ অনুশীলনীর প্রশ্ন ও সমাধান

$\sqrt {A{B^2} - B{C^2}}$

= $\sqrt {{2^2} - {1^2}}$
= 3
∴ cotθ = BC/AC = $\frac{1}{{\sqrt 3 }}$

প্রশ্ন \ 2 \ (i) sin²θ = 1 – cos²θ
(ii) sec²θ = 1 + tan²θ
(iii) cot²θ = 1 – tan²θ
উপরের তথ্যের আলোকে নিম্নের কোনটি সঠিক?
√ i ও ii খ. i ও iii গ. ii ও iii ঘ. i, ii ও iii
ব্যাখ্যা :

নবম অধ্যায় ত্রিকোণমিতিক অনুপাত ৯.২ অনুশীলনী

sin² + cos²θ = 1
∴ sin²θ = 1 – cos²θ

sec²θ – tan²θ = 1
∴ sec²θ = 1 + tan²θ
∴ তথ্যানুসারে i ও ii সঠিক।

চিত্র অনুযায়ী 3 ও 4নং প্রশ্নের উত্তর দাও :
প্রশ্ন \ 3 \ sinθ এর মান কোনটি?
ক. 3/4 খ. 4/3 √ 3/5 ঘ. 4/5
ব্যাখ্যা : AC = $\sqrt {A{B^2} + B{C^2}} {\rm{ = }}\sqrt {{3^2} + {4^2}} {\rm{ = }}\sqrt {25} {\rm{ }}$ = 5
∴ sinθ = AB/AC = 3/5

প্রশ্ন \ 4 \ cotθ এর মান কোনটি?
ক. 3/4 খ. 3/5 গ. 4/5 √ 4/3
ব্যাখ্যা : cotθ = BC/AB = 4/3

⇒ মান নির্ণয় কর (5 – 8)
প্রশ্ন \ 5 \ $\frac{{{\bf{1}} - co{t^2}60^\circ }}{{1 + co{t^2}60^\circ }}$

সমাধান : প্রদত্ত রাশি

\[\begin{array}{l}
= \frac{{1 – co{t^2}60^\circ }}{{1 + co{t^2}60^\circ }}\\
{\rm{ = }}\frac{{1 – {{(cot60^\circ )}^2}}}{{1 + {{(cot60^\circ )}^2}}}{\rm{ }}\\
{\rm{ = }}\frac{{1 – {{\left( {\frac{1}{{\sqrt 3 }}} \right)}^2}}}{{1 + {{\left( {\frac{1}{{\sqrt 3 }}} \right)}^2}}}{\rm{ }}\\
{\rm{ = }}\frac{{1 – \frac{1}{3}}}{{1 + \frac{1}{3}}}\\
= \frac{{\frac{{3 – 1}}{3}}}{{\frac{{3 + 1}}{3}}}\\
= \frac{2}{3} \times \frac{3}{4}\\
= \frac{1}{2}
\end{array}\] (Ans.)

প্রশ্ন \ 6 \ tan45°. sin260°. tan30°. tan60°
সমাধান : প্রদত্ত রাশি = tan45°. sin260°. tan30°. tan60°
\[\begin{array}{l}
{\rm{ = 1 }} \times {\rm{ }}{\left( {\frac{{\sqrt 3 }}{2}} \right)^2} \times \frac{1}{{\sqrt 3 }} \times \sqrt 3 \\
{\rm{ = }}1 \times \frac{3}{4} \times \frac{1}{{\sqrt 3 }} \times \sqrt 3 {\rm{ = }}\frac{3}{4}
\end{array}\](Ans.)

প্রশ্ন \ 7 \ $\frac{{{\bf{1}} - co{s^2}60^\circ }}{{1 + co{s^2}60^\circ }}{\rm{ + sec260}}^\circ$

সমাধান : প্রদত্ত রাশি \[\begin{array}{l}
= \;\frac{{1 – co{s^2}60^\circ }}{{1 + co{s^2}60^\circ }} + {\rm{ }}se{c^2}60^\circ \\
{\rm{ = }}\frac{{1 – {{\left( {\frac{1}{2}} \right)}^2}}}{{1 + {{\left( {\frac{1}{2}} \right)}^2}}} + {(2)^2}\\
= \frac{{1 – \frac{1}{4}}}{{1 + \frac{1}{4}}} + 4{\rm{ }}\\
{\rm{ = }}\frac{{\frac{{4 – 1}}{4}}}{{\frac{{4 + 1}}{4}}} + 4\\
{\rm{ = }}\left( {\frac{3}{4} \times \frac{4}{5}} \right) + 4\\
{\rm{ = }}\frac{3}{5} + 4{\rm{ = }}\frac{{3 + 20}}{5}{\rm{ = }}\frac{{23}}{5}{\rm{ (Ans)}}
\end{array}\]

প্রশ্ন \ 8 \ cos45°.cot²60°.cosec²30°
সমাধান : প্রদত্ত রাশি = cos45°.cot²60°.cosec²30°
\[\begin{array}{l}
{\rm{ = }}\frac{1}{{\sqrt 2 }} \times {\left( {\frac{1}{{\sqrt 3 }}} \right)^2} \times {(2)^2}\\
{\rm{ = }}\frac{1}{{\sqrt 2 }} \times \frac{1}{3} \times 4{\rm{ = }}\frac{{\sqrt 2 \times \sqrt 2 \times 2}}{{\sqrt 2 \times 3}}{\rm{ }}\\
{\rm{ = }}\frac{{2\sqrt 2 }}{3}{\rm{ (Ans}}{\rm{.)}}
\end{array}\]

⇒ দেখাও যে, (9 -15)
প্রশ্ন \ 9 \ cos² 30° – sin² 30° = cos 60°.
সমাধান : আমরা জানি,

\[\begin{array}{l}
{\rm{cos30}}^\circ {\rm{ = }}\frac{{\sqrt 3 }}{2}{\rm{; }}\\
{\rm{cos60}}^\circ {\rm{ = }}\frac{1}{2}\\
sin{\rm{ }}30^\circ = \frac{1}{2}
\end{array}\]
বামপক্ষ \[\begin{array}{l}
co{s^2}30^\circ – si{n^2}30^\circ \\
{\rm{ = }}{\left( {\frac{{\sqrt 3 }}{2}} \right)^{\rm{2}}}{\rm{ – }}{\left( {\frac{1}{2}} \right)^{\rm{2}}}{\rm{ }}\\
{\rm{ = }}\frac{3}{4}{\rm{ – }}\frac{1}{4}\\
{\rm{ = }}\frac{{31}}{4}{\rm{ = }}\frac{2}{4}{\rm{ = }}\\
{\rm{ = }}\frac{1}{2}
\end{array}\]
ডানপক্ষ = cos 60° = 1/2
অর্থাৎ, cos² 30° – sin² 30° = cos 60° (দেখানো হলো)

প্রশ্ন \ 10 \ sin 60° cos 30° + cos 60° sin 30° = sin 90°
সমাধান : আমরা জানি, \[\begin{array}{l}
{\rm{sin 60}}^\circ {\rm{ = }}\frac{{\sqrt 3 }}{2}{\rm{; }}\\
{\rm{sin 30}}^\circ {\rm{ = }}\frac{1}{2}{\rm{; }}\\
{\rm{cos 30}}^\circ {\rm{ = }}\frac{{\sqrt 3 }}{2}\\
{\rm{cos 60}}^\circ {\rm{ = }}\frac{1}{2}
\end{array}\]
এখন, বামপক্ষ \[\begin{array}{l}
= sin{\rm{ }}60^\circ .cos30^\circ + cos60^\circ .sin30^\circ \\
{\rm{ = }}\frac{{\sqrt 3 }}{2} \cdot {\rm{ }}\frac{{\sqrt 3 }}{2}{\rm{ + }}\frac{1}{2} \cdot {\rm{ }}\frac{1}{2}\\
{\rm{ = }}\frac{3}{4}{\rm{ + }}\frac{1}{4}{\rm{ = }}\frac{{3 + 1}}{4}{\rm{ = }}\frac{4}{4}{\rm{ = 1}}
\end{array}\]
ডানপক্ষ = sin90° = 1
অর্থাৎ, sin60°.cos30°+cos60° sin30°= sin90° (দেখানো হলো)

প্রশ্ন \ 11 \ cos 60° cos 30° + sin 60° sin 30° = cos 30°
সমাধান :
বামপক্ষ = cos 60° cos 30° + sin 60° sin 30°
\[\begin{array}{l}
{\rm{ = }}\frac{1}{2} \times {\rm{ }}\frac{{\sqrt 3 }}{2}{\rm{ + }}\frac{{\sqrt 3 }}{2} \times {\rm{ }}\frac{1}{2}\\
{\rm{ = }}\frac{{\sqrt 3 }}{4}{\rm{ + }}\frac{{\sqrt 3 }}{4}{\rm{ = }}\frac{{\sqrt 3 + \sqrt 3 }}{4}\\
{\rm{ = }}\frac{{2\sqrt 3 }}{4}{\rm{ = }}\frac{{\sqrt 3 }}{2}{\rm{ = cos 30}}^\circ {\rm{ }}
\end{array}\]= ডানপক্ষ
অর্থাৎ, cos60°.cos30° + sin60° sin30° = cos30° [ দেখানো হলো ]

প্রশ্ন \ 12 \ sin 3A = cos 3A যদি A = 15° হয়।
সমাধান : দেওয়া আছে, A = 15°
বামপক্ষ = sin 3A
= sin (3 × 15°) = sin 45° = $\frac{1}{{\sqrt 2 }}$

ডানপক্ষ = cos3A
= cos (3 × 15°) = cos 45° = $\frac{1}{{\sqrt 2 }}$
অর্থাৎ, sin3A = cos3A (দেখানো হলো)

প্রশ্ন \ 13 \ sin2A = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} + {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$ যদি A = 45° হয়।
সমাধান : দেওয়া আছে, A = 45°
বামপক্ষ = sin2A = sin(2 × 45°) = sin90° = 1
ডানপক্ষ = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} + {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$
$= \frac{{2tan45^\circ }}{{1 + ta{n^2}45^\circ }}$

${\rm{ = }}\frac{{2 \times 1}}{{1 + 12}}{\rm{ = }}\frac{2}{{1 + 1}} = \frac{2}{2} = 1$

অর্থাৎ, sin2A = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} + {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$ (দেখানো হলো)

প্রশ্ন \ 14 \ tan2A = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} - {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$ যদি A = 30° হয়।
সমাধান : দেওয়া আছে, A = 30°
বামপক্ষ = tan2A
= tan (2 × 30°) = tan60° = $\sqrt 3$

ডানপক্ষ = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} - {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$

$= \frac{{2tan30^\circ }}{{1 - ta{n^2}30^\circ }}{\rm{ }}$

${\rm{ = }}\frac{{2 \times \frac{1}{{\sqrt 3 }}}}{{1 - {{\left( {\frac{1}{{\sqrt 3 }}} \right)}^2}}}{\rm{ }}$

${\rm{ = }}\frac{{\frac{2}{{\sqrt 3 }}}}{{1 - \frac{1}{3}}}{\rm{ = }}\frac{{\frac{2}{{\sqrt 3 }}}}{{\frac{2}{3}}}{\rm{ }}$

${\rm{ = }}\frac{2}{{\sqrt 3 }} \times \frac{3}{2}{\rm{ = }}\frac{{\sqrt 3 \times \sqrt 3 }}{{\sqrt 3 }} = \sqrt 3$

অর্থাৎ, tan2A = $\frac{{{\bf{2tanA}}}}{{{\bf{1}} - {\bf{ta}}{{\bf{n}}^{\bf{2}}}{\bf{A}}}}$ (দেখানো হলো)

প্রশ্ন \ 15 \ cos2A = $\frac{{{\bf{1}} - ta{n^2}A}}{{1 + ta{n^2}A}}$ যদি A = 60° হয়।
সমাধান : দেওয়া আছে, A = 60°
বামপক্ষ = cos2A
= cos(2 × 60°)
= cos120°
= cos (90° + 30°)
= – sin30° = – $\frac{1}{2}$

ডানপক্ষ = $\frac{{{\bf{1}} - ta{n^2}A}}{{1 + ta{n^2}A}}$
= $\frac{{1 - ta{n^2}60}}{{1 + ta{n^2}60}}{\rm{ }}$

= $\frac{{1 - {{\left( {\sqrt 3 } \right)}^2}}}{{1 + {{\left( {\sqrt 3 } \right)}^2}}}$

${\rm{ = }}\frac{{1 - 3}}{{1 + 3}}{\rm{ = }}\frac{{ - 2}}{4}{\rm{ = }} - {\rm{ }}\frac{1}{2}$

অর্থাৎ, cos2A = $\frac{{{\bf{1}} - ta{n^2}A}}{{1 + ta{n^2}A}}$ (দেখানো হলো)

প্রশ্ন \ 16 \ 2 cos(A+B) = 1 = 2 sin(A-B) এবং অ, ই সূক্ষকোণ হলে দেখাও যে, A = 45°, ই = 15°।
সমাধান : দেওয়া আছে, 2cos (A+B) = 1
বা, cos(A+B) = $\frac{1}{2}$
বা, cos(A+B) = cos 60° [∵ cos 60° = $\frac{1}{2}$ ]
বা, A+B = 60° …………………(i)
আবার, 2sin (A-B) = 1
বা, sin (A-B) = $\frac{1}{2}$
বা, sin (A-B) = sin 30° [∵ sin 30° = $\frac{1}{2}$ ]
বা, A-B = 30° …………….(ii)
সমীকরণ (i) ও (ii) যোগ করে পাই,
2A = 90° ∴ A = $\frac{{90^\circ }}{2}$ = 45°
A এর মান সমীকরণ (i)-এ বসিয়ে পাই,
B = 60° – A = 60° – 45° = 15°
∴ A = 45° এবং B = 15° (দেখানো হলো)

প্রশ্ন \ 17 \ cos(A-B) = 1, 2sin(A+B) = 3 এবং অ, ই সূক্ষকোণ হলে, A ও B এর মান নির্ণয় কর।
সমাধান : দেওয়া আছে, cos(A-B) = 1
বা, cos(A-B) = cos0°
∴ A-B = 0°….. ….. ….. ….. ….. (i)
আবার, 2sin(A+B) = $\sqrt 3$

বা, sin(A+B) = $\frac{{\sqrt 3 }}{2}$

বা, sin(A+B) = sin60°
∴ A+B = 60° ….. ….. ….. ….. ….. (ii)
সমীকরণ (i) ও (ii) যোগ করে পাই,
A-B = 0°
A+B = 60°
2A = 60°
বা, A = 60°2

∴ A = 30°
A-এর মান সমীকরণ (ii)-এ বসিয়ে পাই,
30° + B = 60°
বা, B = 60° – 30° ∴ ই = 30°
নির্ণেয় মান A = 30° এবং B = 30°.

প্রশ্ন \ 18 \ সমাধান কর : $\frac{{{\bf{cosA}} - sinA}}{{cosA + sinA}} = \frac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}$

সমাধান : $\frac{{{\bf{cosA}} - sinA}}{{cosA + sinA}} = \frac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}$
বা, $\frac{{cosA - sinA + cosA + sinA}}{{cosA - sinA - cosA - sinA}} = \frac{{\sqrt 3 - 1 + \sqrt 3 + 1}}{{\sqrt 3 - 1 - \sqrt 3 - 1}}$ [যোজন ও বিয়োজন করে]
বা, $\frac{{2cosA}}{{ - 2sinA}} = \frac{{2\sqrt 3 }}{{ - 2}}$

বা, $\frac{{cosA}}{{ - sinA}} = - \sqrt 3$

বা, cotA = $\sqrt 3$
বা, cotA = cot30° ∴ A = 30° (Ans.)

প্রশ্ন \ 19 \ A ও B সূক্ষকোণ এবং cot(A+B) = 1, cot(A-B) = 3 হলে, A ও B এর মান নির্ণয় কর।
সমাধান : 1ম শর্তানুযায়ী
cot(A+B) = 1
বা, cot(A+B) = cot 45° [∵ cot 45° = 1]
∴ A+B = 45° ……………………………(i)
আবার, 2θ শর্তানুযায়ী
cot(A-B) = $\sqrt 3$
বা, cot(A-B) = cot 30° [∵ cot 30° = $\sqrt 3$ ]
∴ A-B = 30°………………………….. (ii)
সমীকরণ (i) ও (ii) যোগ করে পাই,
2A = 75°
বা, A = $\frac{{75^\circ }}{2}$ = ${\rm{37 }}{\frac{1}{2}^ \circ }$

সমীকরণ (i) থেকে পাই,
B = 45 – A
= 45° – $\frac{{75^\circ }}{2}$
= $\frac{{90^\circ - 75^\circ }}{2}$

${\rm{ = }}\frac{{15^\circ }}{2}{\rm{ = 7 }}{\frac{1}{2}^^\circ }$

নির্ণেয় মান A = ${\rm{37 }}{\frac{1}{2}^ \circ }$ ; B = ${\rm{7 }}{\frac{1}{2}^^\circ }$

প্রশ্ন \ 20 \ দেখাও যে, cos3A = 4 cos³A – 3cosA যদি A = 30° হয়।
সমাধান :
বামপক্ষ = cos3A
= cos (3 × 30°)
= cos 90° = 0 [∵ cos90° = 0]
ডানপক্ষ = 4 cos³A – 3cosA
= 4cos³30° – 3cos30°
${\rm{ = 4}} \cdot {\left( {\frac{{\sqrt 3 }}{2}} \right)^3} - 3.\frac{{\sqrt 3 }}{2}$

${\rm{ = }}4.\frac{{3\sqrt 3 }}{8} - \frac{{3\sqrt 3 }}{2}{\rm{ }}$

${\rm{ = }}\frac{{3\sqrt 3 }}{2} - \frac{{3\sqrt 2 }}{2}{\rm{ = 0}}$

অর্থাৎ, cos 3A = 4 cos³A – 3cosA (দেখানো হলো)

প্রশ্ন \ 21 \ সমাধান কর : sinθ + cosθ = 1, যখন 0° ≤ θ ≤ 90°
সমাধান : দেওয়া আছে, sinθ + cos θ = 1
বা, sinθ = 1 – cosθ
বা, sin²θ = (1 – cosθ)² [ বর্গ করে ]
বা, sin²θ = 1 – 2cosθ + cos²θ
বা, 1 – cos²θ = 1 – 2cosθ + cos²θ [∵ sin2θ = 1 – cos²θ]
বা, 1 – cos²θ – 1 + 2cosθ – cos²θ = 0
বা, – 2cos²θ + 2cosθ = 0
বা, – 2cosθ (cosθ – 1) = 0
হয়, – 2cosθ = 0 অথবা, cosθ – 1 = 0
বা, cosθ = $\frac{0}{2} = 0$ বা, cosθ = 1
বা, cosθ = cos90° [∵ cos90° = 0] বা, cosθ = cos 0°
∴ θ = 90° ∴ θ = 0°
নির্ণেয় সমাধান, θ = 0° অথবা 90°

প্রশ্ন \ 22 \ সমাধান কর : cos²θ – sin²θ = 2 – 5 cos θ, যখন θ সূক্ষকোণ।
সমাধান : দেওয়া আছে, cos²θ – sin²θ = 2 – 5 cosθ
বা, cos² θ – sin²θ – 2 + 5 cosθ = 0
বা, cos² θ – (1 – cos²θ) – 2 + 5cosθ = 0 [∵ sin²θ = 1 – cos²θ]
বা, cos² θ – 1 + cos²θ – 2 + 5cosθ = 0
বা, 2 cos²θ + 5cosθ – 3 = 0
বা, 2 cos²θ + 6cosθ – cosθ – 3 = 0
বা, 2cosθ (cosθ + 3) – 1 (cosθ + 3) = 0
বা, (cosθ + 3) (2cosθ – 1) = 0
হয়, cosθ + 3 = 0 অথবা, 2cosθ – 1 = 0
বা, cosθ = – 3 বা, 2cosθ = 1
বা, cosθ = $\frac{1}{2}$

যেহেতু, cosθ এর মান সর্বদা – 1 ও + 1 এর মধ্যবর্তী সুতরাং cosθ = – 3 গ্রহণযোগ্য নয়।
অতএব, cos θ = $\frac{1}{2}$
বা, cosθ = cos60° [∵ cos60° = $\frac{1}{2}$ ]
∴ θ = 60°
নির্ণেয় সমাধান θ = 60°

প্রশ্ন \ 23 \ সমাধান কর : 2sin²θ + 3cosθ – 3 = 0, θ সূক্ষকোণ।
সমাধান : 2sin²θ + 3cosθ – 3 = 0
বা, 2(1 – cos²θ) + 3cosθ – 3 = 0
বা, 2 – 2cos²θ + 3cosθ – 3 = 0
বা, – 2cos²θ + 3cosθ – 1 = 0
বা, 2cos²θ – 3cosθ + 1 = 0 [-1 দ্বারা গুণ করে]
বা, 2cos²θ – 2cosθ – cosθ + 1 = 0
বা, 2cosθ (cosθ – 1) – 1 (cosθ – 1) = 0
বা, (cosθ – 1) (2cosθ – 1) = 0
হয়, cosθ – 1 = 0 অথবা, 2cosθ – 1 = 0
বা, cosθ = 1 = cos0° বা, 2cosθ = 1
∴ θ = 0° বা, cosθ = $\frac{1}{2}$ = cos60°
∴ θ = 60°
নির্ণেয় সমাধান, θ = 60° [যেহেতু θ সূক্ষকোণ]

প্রশ্ন \ 24 \ সমাধান কর : tan²θ – 1 + $\sqrt 3$ tanθ + $\sqrt 3$ = 0
সমাধান : tan²θ – 1 + $\sqrt 3$ tanθ + $\sqrt 3$ = 0
বা, tan²θ – tanθ – $\sqrt 3$ tanθ + $\sqrt 3$ = 0
বা, tanθ (tanθ – 1) – $\sqrt 3$ (tanθ – 1) = 0
বা, (tanθ – 1) (tanθ – $\sqrt 3$ ) = 0
হয় tanθ – 1 = 0 অথবা, tanθ – $\sqrt 3$ = 0
বা, tanθ = 1 = tan45° বা, tanθ = $\sqrt 3$ = tan60°
∴ θ = 45° ∴ θ = 60°
নির্ণেয় সমাধান, θ = 45° এবং 60°
[বি. দ্র. : পাঠ্যবইয়ে উত্তর ভুল আছে]

প্রশ্ন \ 25 \ মান নির্ণয় কর : 3cot²60° + $\frac{{\bf{1}}}{{\bf{4}}}$ cosec²30° + 5sin²45° – 4cos²60°
সমাধান : প্রদত্ত রাশি = 3cot²60° + $\frac{{\bf{1}}}{{\bf{4}}}$ cosec²30° + 5sin² 45° – 4 cos² 60°
\[\begin{array}{l}
{\rm{ = 3 }} \times {\rm{ }}{\left( {\frac{1}{{\sqrt 3 }}} \right)^{\rm{2}}}{\rm{ + }}\frac{1}{4}{\rm{ }} \times {\rm{ (2}}{{\rm{)}}^{\rm{2}}}{\rm{ + 5 }} \times {\rm{ }}{\left( {\frac{1}{{\sqrt 2 }}} \right)^{\rm{2}}}{\rm{ – 4 }} \times {\rm{ }}{\left( {\frac{1}{2}} \right)^{\rm{2}}}\\
{\rm{ = 3 }} \times {\rm{ }}\frac{1}{3}{\rm{ + }}\frac{1}{4} \times {\rm{ 4 + 5 }} \times {\rm{ }}\frac{1}{2}{\rm{ – 4 }} \times {\rm{ }}\frac{1}{4}\\
{\rm{ = 1 + 1 + }}\frac{5}{2}{\rm{ 1 }}\\
{\rm{ = 1 + }}\frac{5}{2}{\rm{ }}\\
{\rm{ = }}\frac{{2 + 5}}{2}{\rm{ }}\\
{\rm{ = }}\frac{7}{2}
\end{array}\]
নির্ণেয় মান $\frac{7}{2}$

প্রশ্ন \ 26 \ ΔABC এর ∠B = 90°, AB = 5 cm, BC = 12 cm
(ক) AC এর দৈর্ঘ্য নির্ণয় কর।
(খ) ∠C = θ হলে sinθ + cosθ এর মান নির্ণয় কর।
(গ) দেখাও যে, sec²θ + cosec²θ = sec²θcosec²θ
সমাধান :
(ক) যেহেতু ∠B = 90°, সেহেতু ABC একটি সমকোণী ত্রিভুজ। AC এর অতিভুজ।

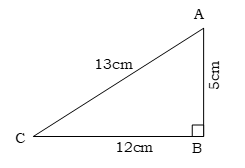
∴পিথাগোরাসের উপপাদ্য অনুসারে পাই,
AC² = AB² + BC²
বা, AC² = (5)² + (12)²
বা, AC² = 25 + 144
বা, AC² = 169
বা, AC = √169
∴ AC = 13cm (Ans.)

(খ) চিত্র হতে পাই,
sinθ = লম্ব/অতিভুজ = AB/AC = 5/13

এবং cosθ = ভুমি/অতিভুজ = BC/AC = 12/13
∴ sinθ + cosθ = $\frac{5}{{13}} + \frac{{12}}{{13}}{\rm{ = }}\frac{{5 + 12}}{{13}}{\rm{ = }}\frac{{17}}{{13}}$

নির্ণেয় মান $\frac{{17}}{{13}}$

(গ) বামপক্ষ

\[\begin{array}{l}
= se{c^2}\theta + {\rm{ }}cose{c^2}\theta \\
{\rm{ = }}\frac{1}{{co{s^2}\theta }} + \frac{1}{{si{n^2}\theta }}{\rm{ }}\\
{\rm{ = }}\frac{{si{n^2}\theta + co{s^2}\theta }}{{si{n^2}\theta co{s^2}\theta }}\\
{\rm{ = }}\frac{1}{{si{n^2}\theta co{s^2}\theta }}\\
{\rm{ = }}{\frac{1}{{co{s^2}\theta }}^.}\frac{1}{{si{n^2}\theta }}\\
= {\rm{ }}se{c^2}\theta .cose{c^2}\theta
\end{array}\] = ডানপক্ষ
অর্থাৎ, sec²θ + cosec²θ = sec²θcosec²θ (দেখানো হলো)

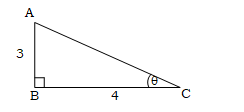
প্রশ্ন \ 27 \

(ক) AC এর পরিমাণ কত?
(খ) tanA + tanC এর মান নির্ণয় কর।
(গ) x ও y এর মান নির্ণয় কর।

সমাধান :
(ক) প্রদত্ত ΔABC একটি সমকোণী ত্রিভুজ।
∴ পিথাগোরাসের উপপাদ্য অনুসারে পাই,
AC² = AB² + BC²
বা, AC² = 1² + (√3)²
বা, AC² = 1 + 3
বা, AC² = 4

বা, AC = √4

∴AC = 2 (Ans.)

(খ) tanA = লম্ব/ভুমি = $\frac{{\sqrt 3 }}{1} = \sqrt 3$

এবং tanC = লম্ব/ভুমি = $\frac{1}{{\sqrt 3 }}$

∴ tanA + tanC = $\sqrt 3 + \frac{1}{{\sqrt 3 }}$

${\rm{ = }}\frac{{3 + 1}}{{\sqrt 3 }}{\rm{ = }}\frac{4}{{\sqrt 3 }}$

নির্ণেয় মান $\frac{4}{{\sqrt 3 }}$

(গ) ‘খ’ হতে পাই, tanA = $\sqrt 3$

বা, tanA = tan60°
বা, A = 60°
বা, x + y = 60° [∵ ∠A = x + y]
∴ x + y = 60° ….. ….. ….. ….. ….. ….. (i)
আবার, tanC = $\frac{1}{{\sqrt 3 }}$
বা, tanC = tan30°
বা, C = 30°
বা, x – y = 30° [∵ ∠C = x – y]
∴ x – y = 30° ….. ….. ….. ….. ….. ….. (ii)
সমীকরণ (i) ও (ii) যোগ করে পাই,
x + y + x – y = 60° + 30°
বা, 2x = 90°
∴ x = $\frac{{90^\circ }}{2}$ = 45°
x এর মান সমীকরণ (i) এ বসিয়ে পাই,
45° + y = 60°
বা, y = 60° – 45° ∴ y= 15°
নির্ণেয় মান x = 45° এবং y = 15°