এসএসসি বা নবম দশম শ্রেণির গণিত সমাধান অংশে আজকের আয়োজন নবম দশম শ্রেণির গণিত সমাধান অনুশীলনী 11.2। এখানে আপনারা নবম দশম শ্রেণির গণিত বইয়ের সমাধান হিসেবে সকল অধ্যায়ের সমাধান পেয়ে যাবেন। নবম দশম শ্রেণির গণিত সৃজনশীল প্রশ্ন ও নবম দশম শ্রেণীর গণিত mcq সমাধান ও আমাদের সাইটে পেয়ে যাবেন যার লিংক নিচে দেওয়া হয়েছে।

নবম ও দশম শ্রেণীর গণিত সমাধান অনুশীলনী ১১.২

বি.দ্র: পোস্টটি সঠিকভাবে দেখতে google chrome অথবা প্রতিষ্ঠিত কোন ব্রাউজার ব্যবহার করুন।

1. a, b, c ক্রমিক সমানুপাতী হলে নিচের কোনটি সঠিক?
ক. a2 = bc ✅ b2 = ac গ. ab = bc গ. a = b = c

2. আরিফ ও আকিবের বয়সের অনুপাত 5 : 3; আরিফের বয়স 20 বছর হলে, কত বছর পর তাদের বয়সের অনুপাত 7 : 5 হবে?
ক. 5 বছর খ. 6 বছর ✅ 8 বছর ঘ. 10 বছর
ব্যাখ্যা : ধরি, আরিফের বয়স 5x এবং আকিবের বয়স 3x
প্রশ্নমতে, 5x = 20
∴ x = 4
∴ আকিবের বয়স = (3 × 4) বছর = 12 বছর
আবার, ধরি, y বছর পর তাদের বয়সের অনুপাত 7 : 5 হবে
∴ \[\frac{{20 + y}}{{12 + y}}{\rm{ = }}\frac{7}{5}\]

বা, 100 + 5y = 84 + 7y
বা, 7y – 5y = 100 – 84
বা, 2y = 16
∴ y = 8
∴ 8 বছর পর বয়সের অনুপাত 7 : 5 হবে।

3. নিচের তথ্যগুলো লক্ষ কর :
i. সমানুপাতের চারটি রাশিই একজাতীয় হওয়ার প্রয়োজন হয় না।
ii. দুইটি ত্রিভুজ ক্ষেত্রের ক্ষেত্রফলের অনুপাত তাদের ভূমিদ্বয়ের অনুপাতের সমান।
iii. \[\frac{a}{b}{\rm{ = }}\frac{c}{d}{\rm{ = }}\frac{e}{f}{\rm{ = }}\frac{g}{h}\]  হলে, এদের প্রতিটি অনুপাতের মান \[\frac{{a + c + e + g}}{{b + d + f + h}}\]

উপরের তথ্যগুলোর ভিত্তিতে নিচের কোনটি সঠিক?
ক.i ও ii খ.ii ও iii ✅i ও iii ঘ. i, ii ও iii

ব্যাখ্যা : ii সঠিক নয়; কারণ, দুইটি ত্রিভুজ ক্ষেত্রের ক্ষেত্রফলের অনুপাত তাদের ভূমিদ্বয়ের অনুপাতের সমান হবে। যদি তাদের উচ্চতা সমান হয়। কিন্তু এখানে উচ্চতার কথা বলা হয় নি।

ΔABC এর কোণগুলোর অনুপাত 2 : 3 : 5 এবং ABCD চতুর্ভুজের কোণ চারটির অনুপাত 3 : 4 : 5 : 6; তথ্যের ভিত্তিতে 4 ও 5 নং প্রশ্নের উত্তর দাও।
4. একটি বর্গের বাহুর দৈর্ঘ্য দ্বিগুণ হলে তার ক্ষেত্রফল কতগুণ বৃদ্ধি পাবে?
ক. 2 গুণ ✅ 4 গুণ গ. 8 গুণ ঘ. 6 গুণ
ব্যাখ্যা : ধরি, বর্গের এক বাহুর দৈর্ঘ্য x
∴ ক্ষেত্রফল = x² বর্গ একক
দৈর্ঘ্য দ্বিগুণ হলে বাহুর দৈর্ঘ্য = 2x
∴ ক্ষেত্রফল = (2x)² বর্গ একক = 4x² বর্গ একক

5. x : y = 7 : 5, y : z = 5 : 7 হলে, x : z = কত?
ক. 35 : 49 ✅ 35 : 35
গ. 25 : 49 ঘ. 49 : 25

প্রশ্ন \ 6 \ একটি কাঠের পুল তৈরির প্রাক্কলিত ব্যয় 90,000 টাকা। কিন্তু খরচ বেশি হয়েছে 21,600 টাকা। খরচ শতকরা কত বৃদ্ধি পেয়েছে?
সমাধান : দেওয়া আছে, প্রাক্কলিত ব্যয় = 90,000 টাকা
খরচ বৃদ্ধি = 21600 টাকা

∴ শতকরা খরচ বৃদ্ধি =( প্রাক্কলিত ব্যয়/খরচ বৃদ্ধি) × 100 %
= \[\left( {\frac{{90000}}{{21600}} \times 100} \right)\% = 24\% \]
∴ খরচ 24% বৃদ্ধি পেয়েছে। (ans)

প্রশ্ন \ 7 \ ধানে চাল ও তুষের অনুপাত 7 : 3 হলে, এতে শতকরা কী পরিমাণ চাল আছে?
সমাধান : দেওয়া আছে, চাল : তুষ = 7 : 3
মনে করি, ধানে চালের পরিমাণ = 7x
এবং তুষের পরিমাণ = 3x
তাহলে, ধানের ওজন হবে (7x + 3x) বা 10x
ধানে চালের শতকরা পরিমাণ = চালের পরিমাণ/ ধানের পরিমাণ × 100 %
\[ = \left( {\frac{{7x}}{{10x}} \times 100} \right)\% \; = {\rm{ }}70\% \]∴ ধানে 70% চাল আছে। (ans)

প্রশ্ন \ 8 \ 1 ঘন সে.মি. কাঠের ওজন 7 ডেসিগ্রাম। কাঠের ওজন সমআয়তন পানির ওজনের শতকরা কত ভাগ?
সমাধান :
1 ঘন সে.মি. কাঠের ওজন = 7 ডেসিগ্রাম
1 ঘন সে.মি. পানির ওজন = 1 গ্রাম = 10 ডেসিগ্রাম
এখন, 1 ঘন সে.মি. কাঠের ওজন/1 ঘন সে.মি. পনির ওজন =\[\frac{7}{{10}}\]

∴কাঠের ওজন এবং সমআয়তনের পানির ওজনের শতকরা

\[{\rm{ = }}\left( {\frac{7}{{10}} \times 100} \right)\% {\rm{ = 70}}\% \]

∴ কাঠের ওজন সমআয়তন পানির ওজনের 70% (ans)

প্রশ্ন \ 9 \ ক, খ, গ, ঘ এর মধ্যে 300 টাকা এমনভাবে ভাগ করে দাও যেন, ক এর অংশ : খ এর অংশ = 2 : 3, খ এর অংশ : গ এর অংশ = 1 : 2 এবং গ এর অংশ : ঘ এর অংশ = 3 : 2 হয়।
সমাধান : এখানে,
ক এর অংশ : খ এর অংশ = 2 : 3
খ এর অংশ : গ এর অংশ = 1 : 2 = (1 × 3) : (2 × 3) = 3 : 6
গ এর অংশ : ঘ এর অংশ = 3 : 2 = (3 × 2) : (2 × 2) = 6 : 4
∴ ক এর অংশ : খ এর অংশ : গ এর অংশ : ঘ এর অংশ
= 2 : 3 : 6 : 4
∴ অনুপাতের রাশিগুলোর যোগফল = 2 + 3 + 6 + 4 = 15
∴ ক এর অংশ = 300 এর ২/১৫ টাকা = 40 টাকা
খ এর অংশ = 300 এর ৩/১৫ টাকা = 60 টাকা
গ এর অংশ = 300 এর  ৬/১৫ টাকা = 120 টাকা
এবং ঘ এর অংশ = 300 এর ৪/১৫ টাকা = 80 টাকা
∴ ক 40 টাকা, খ 60 টাকা, গ 120 টাকা এবং ঘ 80 টাকা পায়। (ans)

প্রশ্ন \ 10 \ তিনজন জেলে 690 টি মাছ ধরেছে। তাদের অংশের অনুপাত

, এবং হলে, কে কয়টি মাছ পেল?
সমাধান : দেওয়া আছে, মোট মাছের সংখ্যা = 690 টি
তিনজনের অংশের অনুপাত = \[\frac{2}{3}:\frac{4}{5}:\frac{5}{6}\]

\[{\rm{ = }}\left( {\frac{2}{3} \times 30} \right):\left( {\frac{4}{5} \times 30} \right):\left( {\frac{5}{6} \times 30} \right)\]

[3, 5 ও 6 এর ল. সা. গু. 30 দিয়ে গুণ করে]
= 20 : 24 : 25
∴ অনুপাতের রাশিগুলোর যোগফল = 20 + 24 + 25 = 69
∴ 1ম জেলের মাছের সংখ্যা = 690 এর ২০/৬৯ টি = 200 টি
2য় জেলের মাছের সংখ্যা = 690 এর ২৪/৬৯ টি = 240 টি
এবং 3য় জেলের মাছের সংখ্যা = 690 এর ২৫/৬৯ টি = 250 টি
∴ তিনজন জেলে যথাক্রমে 200 টি, 240 টি এবং 250 টি মাছ পেল। (ans)

প্রশ্ন \ 11 \ একটি ত্রিভুজের পরিসীমা 45 সে. মি.। বাহুগুলোর দৈর্ঘ্যরে অনুপাত 3 : 5 : 7 হলে, প্রত্যেক বাহুর পরিমাণ নির্ণয় কর।
সমাধান : দেওয়া আছে, ত্রিভুজের পরিসীমা = 45 সে. মি.
এবং বাহুগুলোর দৈর্ঘ্যরে অনুপাত = 3 : 5 : 7
∴ অনুপাতের রাশিগুলোর যোগফল = 3 + 5 + 7 = 15
∴ ত্রিভুজের প্রথম বাহুর দৈর্ঘ্য 45 এর ৩/১৫ সে. মি.
= 9 সে. মি.
ত্রিভুজের দ্বিতীয় বাহুর দৈর্ঘ্য 45 এর ৫/১৫ সে. মি.
= 15 সে. মি.
এবং ত্রিভুজের তৃতীয় বাহুর দৈর্ঘ্য 45 এর ৭/১৫ সে. মি.
= 21 সে. মি.
নির্ণেয় ত্রিভুজের বাহুগুলোর পরিমাণ 9 সে. মি., 15 সে. মি. ও 21 সে. মি.।

প্রশ্ন \ 12 \ 1011 টাকাকে \[\frac{{\bf{3}}}{{\bf{4}}}:\frac{{\bf{4}}}{{\bf{5}}}:\frac{{\bf{6}}}{{\bf{7}}}\] অনুপাতে বিভক্ত কর।
সমাধান : দেওয়া আছে, মোট টাকার পরিমাণ 1011
এবং বণ্টনের অনুপাত = \[\frac{{\bf{3}}}{{\bf{4}}}:\frac{{\bf{4}}}{{\bf{5}}}:\frac{{\bf{6}}}{{\bf{7}}}\]
= \[\left( {\frac{3}{4} \times 140} \right):\left( {\frac{4}{5} \times 140} \right):\left( {\frac{6}{7} \times 140} \right)\] [হর 4, 5 ও 7 এর ল.সা.গু. 140 দ্বারা গুণ করে]
= 105 : 112 : 120
∴ অনুপাতের রাশিগুলোর সমষ্টি = 105 + 112 + 120 = 337
∴ প্রথম অংশ = 1011 এর 105/337 টাকা = 315 টাকা
দ্বিতীয় অংশ = 1011 এর 112/337  টাকা = 336 টাকা
তৃতীয় অংশ = 1011 এর 120/337  টাকা = 360 টাকা
∴ বিভক্তকৃত টাকার পরিমাণ 315 টাকা, 336 টাকা, 360 টাকা। (ans)

প্রশ্ন \ 13 \ দুইটি সংখ্যার অনুপাত 5 : 7 এবং তাদের গ. সা. গু. 4 হলে, সংখ্যা দুইটির ল.সা.গু. কত?
সমাধান : দেওয়া আছে, সংখ্যা দুইটির অনুপাত 5 : 7
মনে করি, সংখ্যা দুইটি 5x ও 7x, যেখানে, x অনুপাতের সাধারণ গুণিতক।
5x ও 7x এর গ. সা. গু. x
প্রশ্নানুসারে, x = 4
5x ও 7x এর ল. সা. গু. = 35x = 35 × 4 [∵ x = 4]
= 140
অতএব, সংখ্যা দুইটির ল. সা. গু. 140 (ans)

প্রশ্ন \ 14 \ ক্রিকেট খেলায় সাকিব, মুশফিকুর ও মাশরাফী 171 রান করলো। সাকিব ও মুশফিকুরের এবং মুশফিকুর ও মাশরাফীর রানের অনুপাত 3 : 2 হলে কে কত রান করেছে?
সমাধান : সাকিবের রান : মুশফিকুরের রান = 3 : 2
= (3 × 3) : (2 × 3)
= 9 : 6
মুশফিকুরের রান : মাশরাফীর রান = 3 : 2
= (3 × 2) : (2 × 2)
= 6 : 4
∴ সাকিবের রান : মুশফিকুরের রান : মাশরাফীর রান = 9 : 6 : 4
অনুপাতের রাশিগুলোর যোগফল = 9 + 6 + 4 = 19
∴ সাকিবের রান 171 এর 9/19 = 171 × 9/19 রান = 81 রান
মুশফিকুরের রান 171 এর 6/19 = 171 × 6/19 রান = 54 রান
মাশরাফীর রান 171 এর 4/19 = 171 × 4/19 রান = 36 রান
∴ সাকিব 81 রান, মুশফিকুর 54 রান, মাশরাফী 36 রান করেছে।(ans)

প্রশ্ন \ 15 \ একটি অফিসে 2 জন কর্মকর্তা, 7 জন করণিক এবং 3 জন পিওন আছে। একজন পিওন 1 টাকা পেলে একজন করণিক পায় 2 টাকা, একজন কর্মকর্তা পায় 4 টাকা। তাদের সকলের মোট বেতন 150,000 টাকা হলে, কে কত বেতন পায়?
সমাধান : মনে করি, একজন পিওন পায় x টাকা (সমানুপাতিক x ধরে)
তাহলে, একজন করণিক পায় 2x টাকা
এবং একজন কর্মকর্তা পায় 4x টাকা।
প্রশ্নমতে, (4x × 2) + (2x × 7) + (x × 3) = 150000
বা, 8x + 14x + 3x = 150000
বা, 25x = 150000
বা, x = \[\frac{{150000}}{{25}}\]

∴ x = 6000
∴ একজন পিওনের বেতন = 6000 টাকা
একজন করণিকের বেতন = (6000 × 2) টাকা = 12000 টাকা
এবং একজন কর্মকর্তার বেতন = (6000 × 4) টাকা = 24000 টাকা
∴ প্রত্যেক কর্মকর্তা 24000 টাকা, করণিক 12000 টাকা এবং পিওন 6000 টাকা বেতন পায়। (ans)

প্রশ্ন \ 16 \ একটি সমিতির নেতা নির্বাচনে দুইজন প্রতিদ্বন্দীর মধ্যে ডোনাল্ড সাহেব 4 : 3 ভোটে জয়লাভ করলেন। যদি মোট সদস্য সংখ্যা 581 হয় এবং 91 জন সদস্য ভোট না দিয়ে থাকেন, তবে ডোনাল্ড সাহেবের প্রতিদ্বন্দী কত ভোটের ব্যবধানে পরাজিত হয়েছেন?
সমাধান : দেওয়া আছে, মোট সদস্য = 581 জন
91 জন সদস্য ভোট না দেওয়ায় ভোট দেওয়া সদস্য
(581 – 91) জন = 490 জন
ডোনাল্ড সাহেবের প্রাপ্ত ভোট : প্রতিদ্বন্দীর প্রাপ্ত ভোট = 4 : 3
অনুপাতের রাশিদ্বয়ের যোগফল = 4 + 3 = 7
∴ ডোনাল্ড সাহেব পেলেন 490 এর  4/7 ভোট = 280 ভোট
এবং প্রতিদ্বন্দী পেলেন 490 এর 3/7 ভোট = 210 ভোট
∴ ডোনাল্ড সাহেবের প্রতিদ্বন্দী পরাজিত হলেন (280 – 210) বা, 70 ভোটের ব্যবধানে। (ans)

প্রশ্ন \ 17 \ যদি কোনো বর্গক্ষেত্রের বাহুর পরিমাণ 20% বৃদ্ধি পায়, তবে তার ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?
সমাধান : মনেকরি, বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য x একক
∴ বর্গক্ষেত্রের ক্ষেত্রফল x² বর্গ একক.
20% বৃদ্ধিতে বর্গক্ষেত্রের বাহুর দৈর্ঘ্য (x + x এর 20/100) একক
= \[\left( {x + \frac{x}{5}} \right)\] একক

= \[\frac{{6x}}{5}\] একক
∴ 20% বৃদ্ধিতে বর্গক্ষেত্রের ক্ষেত্রফল \[{\left( {\frac{{6x}}{5}} \right)^2}\] বর্গ একক
= \[\frac{{36{x^2}}}{{25}}\] বর্গ একক
বর্গক্ষেত্রের ক্ষেত্রফল বৃদ্ধি \[\left( {\frac{{36{x^2}}}{{25}} – {x^2}} \right)\] বর্গ একক
= \[\left( {\frac{{36{x^2} – 25{x^2}}}{{25}}} \right)\] বর্গ একক
= \[\frac{{11{x^2}}}{{25}}\] বর্গ একক
∴ শতকরা ক্ষেত্রফল বৃদ্ধি মোট বৃদ্ধি/পূর্বের ক্ষেত্রফল × 100%
= \[\left( {\frac{{\frac{{11{x^2}}}{{25}}}}{{{x^2}}} \times 100} \right)\] %
= 44%
∴ ক্ষেত্রফল বৃদ্ধি পায় 44% (ans)

প্রশ্ন \ 18 \ একটি আয়তক্ষেত্রের দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস পেলে আয়তক্ষেত্রের ক্ষেত্রফল শতকরা কত বৃদ্ধি বা হ্রাস পাবে?
সমাধান : মনে করি, আয়তক্ষেত্রের দৈর্ঘ্য x একক এবং প্রস্থ ু একক
∴ আয়তক্ষেত্রটির ক্ষেত্রফল = xy বর্গ একক
10% বৃদ্ধিতে আয়তক্ষেত্রের দৈর্ঘ্য = x + x এর 10/100 একক
= x + x/100 একক
= 11x/100 একক
এবং 10% হ্রাসে আয়তক্ষেত্রের প্রস্থ = y-y এর 10/100 একক
= y- y/10 একক
= 9y/10 একক
∴ 10% হ্রাস-বৃদ্ধিতে আয়তক্ষেত্রের ক্ষেত্রফল = \[\frac{{11x}}{{10}} \times \frac{{9y}}{{10}}\] বর্গ একক
= \[\frac{{99xy}}{{100}}\] বর্গ একক
সুতরাং ক্ষেত্রফল হ্রাস পায় \[\left( {xy – \frac{{99xy}}{{100}}} \right)\]  বর্গ একক
= \[\left( {\frac{{100xy – 99xy}}{{100}}} \right)\] বর্গ একক
= \[\frac{{xy}}{{100}}\] বর্গ একক
∴ ক্ষেত্রফল শতকরা হ্রাস পায় = মোট হ্রাস/পূর্বের ক্ষেত্রফল × 100 বর্গ একক
= \[\left( {\frac{{\frac{{xy}}{{100}}}}{{xy}} \times 100} \right)\] বর্গ একক
= \[\frac{{xy}}{{100}} \times \frac{1}{{xy}} \times {\rm{100}}\] বর্গ একক
= 1 বর্গ একক
অতএব, আয়তক্ষেত্রের ক্ষেত্রফল 1% হ্রাস পাবে। (ans)

প্রশ্ন \ 19 \ একটি মাঠের জমিতে সেচের সুযোগ আসার আগের ও পরের ফলনের অনুপাত 4 : 7. ঐ মাঠে যে জমিতে আগে 304 কুইণ্টাল ধান ফলতো, সেচ পাওয়ার পরে তার ফলন কত হবে?
সমাধান : মনেকরি, সেচ পাওয়ার পরে ফলনের পরিমাণ ী কুইন্টাল
সেচ আসার আগের ফলন : সেচ আসার পরের ফলন = 4 : 7
প্রশ্নানুসারে, 304 : x = 4 : 7
বা, \[\frac{{304}}{x}{\rm{ = }}\frac{4}{7}\]

বা, 4x = 7 × 304
বা, x = \[\frac{{7 \times 304}}{4}\]

∴ x = 532
∴ সেচ পাওয়ার পরে ফলন হবে 532 কুইন্টাল। (ans)

প্রশ্ন \ 20 \ ধান ও ধান থেকে উৎপন্ন চালের অনুপাত 3 : 2 এবং গম ও গম থেকে উৎপন্ন সুজির অনুপাত 4 : 3 হলে, সমান পরিমাণের ধান ও গম থেকে উৎপন্ন চাল ও সুজির অনুপাত বের কর।
সমাধান : মনে করি, উৎপন্ন চালের পরিমাণ x কুইন্টাল
এবং উৎপন্ন সুজির পরিমাণ y কুইন্টাল
প্রশ্নানুসারে, ধান : চাল = 3 : 2
বা, 1 : x = 3 : 2
বা, \[\frac{1}{x}{\rm{ = }}\frac{3}{2}\]

∴ x = 2/3

∴ চালের পরিমাণ 2/3 কুইন্টাল
আবার, গম : সুজি = 4 : 3
বা, 1 : y = 4 : 3
বা, \[\frac{1}{y}{\rm{ = }}\frac{4}{3}\]

∴ y = 3/4

∴ সুজির পরিমাণ 3/4 কুইন্টাল।
উৎপন্ন চাল : উৎপন্ন সুজি = 2/3 : 3/4

\[{\rm{ = }}\left( {\frac{2}{3} \times 12} \right):\left( {\frac{3}{4} \times 12} \right)\]  [3, 4 এর ল.সা.গু. 12]
= 8 : 9
∴ উৎপন্ন চাল ও সুজির অনুপাত 8 : 9। (ans)

প্রশ্ন \ 21 \ একটি জমির ক্ষেত্রফল 432 বর্গমিটার। ঐ জমির দৈর্ঘ্য ও প্রস্থের সঙ্গে অপর একটি জমির দৈর্ঘ্য ও প্রস্থের অনুপাত যথাক্রমে 3 : 4 এবং 2 : 5 হলে, অপর জমির ক্ষেত্রফল কত?
সমাধান : দেওয়া আছে,
1ম জমির দৈর্ঘ্য : 2য় জমির দৈর্ঘ্য = 3 : 4
এবং 1ম জমির প্রস্থ : 2য় জমির প্রস্থ = 2 : 5
ধরি, 1ম জমির দৈর্ঘ্য = 3x মিটার
2য় জমির দৈর্ঘ্য = 4x মিটার
এবং 1ম জমির প্রস্থ = 2y মিটার
2য় জমির প্রস্থ = 5y মিটার
1ম জমির ক্ষেত্রফল = (3x × 2y) বর্গমিটার
= 6xy বর্গমিটার
2য় জমির ক্ষেত্রফল = (4x × 5y) বর্গমিটার
= 20xy বর্গমিটার
প্রশ্নমতে, 6xy          = 432
বা, xy = 432/6

∴ xy = 72
∴ 2য় জমির ক্ষেত্রফল = 20xy বর্গমিটার
= (20 × 72) ব.মি. [∵ xy = 72]
= 1440 বর্গমিটার
∴ অপর জমির ক্ষেত্রফল 1440 বর্গমিটার। (ans)

প্রশ্ন \ 22 \ জেমি ও সিমি একই ব্যাংক থেকে একই দিনে 10% হার সরল মুনাফায় আলাদা আলাদা পরিমাণ অর্থ ঋণ নেয়। জেমি 2 বছর পর মুনাফা-আসলে যত টাকা শোধ করে 3 বছর পর সিমি মুনাফা-আসলে তত টাকা শোধ করে। তাদের ঋণের অনুপাত নির্ণয় কর।
সমাধান : মনে করি, ব্যাংক থেকে জেমি ঋণ করে x টাকা এবং
সিমি ঋণ করে y টাকা
এখন, 10% মুনাফায় x টাকার 2 বছরের মুনাফা
= x × 2 × 10/100 টাকা = x/5 টাকা
∴ 2 বছর পরে জেমি মুনাফা-আসলে পরিশোধ করে = x + x/5 টাকা
= \[\frac{{5x + x}}{5}\] টাকা
= 6x/5 টাকা
আবার, 10% মুনাফায় y টাকার 3 বছরের মুনাফা
= y × 3 × 10/100 টাকা
= 3y/10 টাকা
∴ 3 বছর পরে সিমি মুনাফা-আসলে পরিশোধ করে = y + 3y/10 টাকা
= \[\frac{{10y + 3y}}{{10}}\] টাকা
= 13y/10 টাকা
প্রশ্নানুসারে, 6x/5 = 13y/10
বা, 60x = 65y
বা, \[\frac{x}{y}{\rm{ = }}\frac{{65}}{{60}}\]

বা, \[\frac{x}{y}{\rm{ = }}\frac{{13}}{{12}}\]

∴x : y = 13 : 12
নির্ণেয় ঋণের অনুপাত 13 : 12

প্রশ্ন \ 23 \ একটি ত্রিভুজের বাহুগুলোর অনুপাত 5:12:13 এবং পরিসীমা 30 সে. মি.
ক. ত্রিভুজটি অঙ্কন কর এবং কোণভেদে ত্রিভুজটি কী ধরনের তা লিখ।
খ. বৃহত্তর বাহুকে দৈর্ঘ্য এবং ক্ষুদ্রতর বাহুকে প্রস্থ ধরে অঙ্কিত আয়তক্ষেত্রের কর্ণের সমান বাহুবিশিষ্ট বর্গের ক্ষেত্রফল নির্ণয় কর।
গ. উক্ত আয়তক্ষেত্রের দৈর্ঘ্য 10% এবং প্রস্থ 20% বৃদ্ধি পেলে ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?

সমাধান :
ক. দেওয়া আছে, ত্রিভুজের বাহুগুলোর অনুপাত 5 : 12 : 13 এবং পরিসীম 30 সে.মি.।
ধরি, ত্রিভুজের বাহুগুলো 5x, 12x ও 13x সে.মি.
প্রশ্নমতে, 5x + 12x + 13x = 30
বা, 30x = 30
∴ x = 1
অতএব, ত্রিভুজের বাহুগুলো হলো 5 সে.মি., 12 সে.মি. ও 13 সে.মি.।

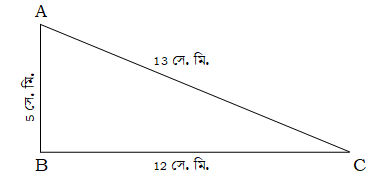
চিত্র হতে, AB² + BC² = (5)² + (12)²
= 25 + 144 = 169 = (13)² = (AC)²
∴ পিথাগোরাসের উপপাদ্য অনুযায়ী ত্রিভুজটি সমকোণী। অতএব, ত্রিভুজটি একটি সমকোণী ত্রিভুজ এবং ∠ABC = 90°

খ. বৃহত্তর বাহুর দৈর্ঘ্য 13 সে. মি. কে দৈর্ঘ্য এবং ক্ষুদ্রতর বাহুর দৈর্ঘ্য 5 সে. মি. কে প্রস্থ ধরে নিচে আয়তক্ষেত্রটি আঁকা হলো :

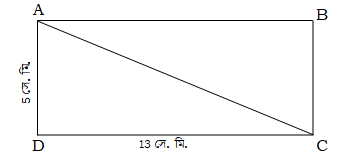
ABCD আয়তক্ষেত্রের কর্ণ অঈ কোনো বর্গক্ষেত্রের বাহু হলে ঐ বর্গক্ষেত্রটির ক্ষেত্রফল হবে AC² বর্গ সে. মি.
এখন, ΔADC এ ∠D = 90°
∴ পিথাগোরাসের উপপাদ্য অনুসারে পাই, AC² = AD² + CD²
= (5)² + (13)²
= 25 + 169
= 194
অর্থাৎ, ঐ বর্গক্ষেত্রটির ক্ষেত্রফল 194 বর্গ সে. মি. (ans)

গ. 10% বৃদ্ধিতে আয়তক্ষেত্রটির দৈর্ঘ্য
= 13 + 13 এর 10/100 সে. মি.
= 13 + 1310 সে. মি.
= 143/10 সে. মি.
= 14.3 সে. মি.
এবং 20% বৃদ্ধিতে আয়তক্ষেত্রটির প্রস্থ
= 5 + 5 এর 20/100 সে. মি.
= (5 + 1) সে. মি.
= 6 সে. মি.
∴ দৈর্ঘ্য-প্রস্থ বৃদ্ধিতে আয়তক্ষেত্রটির ক্ষেত্রফল
= (14.3 × 6) বর্গ সে. মি.
= 85.8 বর্গ সে. মি.
দৈর্ঘ্য 13 সে. মি. এবং প্রস্থ 5 সে. মি. বিশিষ্ট আয়তক্ষেত্রটির ক্ষেত্রফল = (13 × 5) বর্গ সে. মি. = 65 বর্গ সে. মি.
∴ ক্ষেত্রফল বৃদ্ধি পায় (85.5 – 65) বর্গ সে.মি.
= 20.8 বর্গ সে.মি.
∴ ক্ষেত্রফল শতকরা বৃদ্ধি পাবে (ক্ষেত্রফল বৃদ্ধি/আদি ক্ষেত্রফল) × 100%
= \[\left( {\frac{{20 \cdot 8}}{{65}} \times 100} \right)\] %
= 32%
অতএব, ক্ষেত্রফল 32% বৃদ্ধি পাবে।

প্রশ্ন \ 24 \ একদিন কোনো ক্লাসে অনুপস্থিত ও উপস্থিত শিক্ষার্থীর অনুপাত 1 : 4।
ক. অনুপস্থিত শিক্ষার্থীদেরকে মোট শিক্ষার্থীর শতকরায় প্রকাশ কর।
খ. 10 জন শিক্ষার্থী বেশি উপস্থিত হলে অনুপস্থিত ও উপস্থিত শিক্ষার্থীর অনুপাত হতো 1 : 9। মোট শিক্ষার্থীর সংখ্যা কত?
গ. মোট শিক্ষার্থীর মধ্যে ছাত্র সংখ্যা ছাত্রী সংখ্যার দ্বিগুণ অপেক্ষা 20 জন কম। ছাত্র ও ছাত্রীসংখ্যার অনুপাত নির্ণয় কর।

সমাধান :
ক. মনে করি, অনুপস্থিত ছাত্র সংখ্যা x
এবং উপস্থিত ছাত্রসংখ্যা 4x [এখানে, x ধনাত্মক আনুপাতিক ধ্রুবক]
মোট ছাত্র সংখ্যা = x + 4x = 5x
∴ অনুপস্থিত ছাত্রসংখ্যা মোট ছাত্রসংখ্যার x/5x ভাগ
অর্থাৎ, অনুপস্থিত ছাত্রমোট ছাত্র × 100%
=x/5x × 100% = 1/5 × 100% = 20%
∴ অনুপস্থিত ছাত্রসংখ্যা মোট ছাত্র সংখ্যার 20%

খ. 10 জন শিক্ষার্থী বেশি উপস্থিত হলে,
উপস্থিত শিক্ষার্থী সংখ্যা হয় (4x + 10) জন
অনুপস্থিত শিক্ষার্থী সংখ্যা (x – 10) জন
প্রশ্নানুসারে, (x – 10) : (4x + 10) = 1 : 9
বা, \[\frac{{x – 10}}{{4x + 10}}{\rm{ = }}\frac{1}{9}\] বা, 9ী – 90 = 4x + 10
বা, 9ী – 4x = 90 + 10
বা, 5x = 100
বা, x = 100/5

∴ x = 20
∴ মোট শিক্ষার্থী 5x = (5 × 20) জন = 100 জন (ans)

গ. ধরি, ছাত্রী সংখ্যা = y জন
এবং ছাত্র সংখ্যা = (2y – 20) জন
প্রশ্নানুসারে, y + 2y – 20 = 100
বা, 3y = 100 + 20
বা, 3y = 120
বা, y = 120/3

∴ y = 40
∴ ছাত্রী সংখ্যা 40 জন।
∴ ছাত্র সংখ্যা = 2y – 20 = (2 × 40 – 20) জন = 60 জন
∴ ছাত্র : ছাত্রx = 60 : 40 [20 দ্বারা ভাগ করে]
= 3 : 2
নির্ণেয় অনুপাত 3 : 2

২৫. আশিক, মিজান, অনিকা ও অহনা মোট 195000 টাকা মূলধন নিয়ে একটি ব্যবসা শুরু করে এবং এক বছর শেষে 26500 টাকা লাভ হয়। উক্ত ব্যবসায় মূলধনে আশিকের অংশ : মিজানের অংশ=2 : 3, মিজানের অংশ : অনিকার অংশ=4 : 5 এবং অনিকার অংশ : অহনার অংশ= 5 : 6

ক) মূলধনের সরল অনুপাত নির্ণয় কর।

সমাধানঃ ব্যবসাটিতে বিনিয়োগকৃত মূলধনে,

আশিকের অংশ : মিজানের অংশ=2 : 3 = 8 : 12

মিজানের অংশ : আনিকার অংশ=4 : 5 = 12 : 15

অনিকার অংশ : অহনার অংশ= 5 : 6 =15 : 18

∴ আশিকের অংশ : মিজানের অংশ : আনিকার অংশ : অহনার অংশ=8 : 12 : 15 : 18

খ) উক্ত ব্যবসায় প্রত্যেকের মূলধন নির্ণয় কর।

সমাধানঃ ক হতে পাই,

আশিকের অংশ : মিজানের অংশ : আনিকার অংশ : অহনার অংশ=8 : 12 : 15 : 18

অনুপাতগুলোর যোগফল=8+12+15+18=53

মোট মূলধন=195000 টাকা।

তাহলে,

আশিকের মূলধন=195000 এর (8/53) টাকা = 29433.96 টাকা

মিজানের মূলধন=195000 এর (12/53) টাকা = 44150.944 টাকা

অনিকার মূলধন=195000 এর (15/53) টাকা = 55188.68 টাকা

অহনার মূলধন=195000 এর (18/53) টাকা = 66226.42 টাকা

গ) বছর শেষে লভ্যাংশের 60% উক্ত ব্যবসায় বিনিয়োগ করা হল। অবশিষ্ট লভ্যাংশ মূলধনের সরল অনুপাতে বিভক্ত হলে অহনা ও আশিকের লভ্যাংশের মধ্যে কে কত টাকা বেশি লাভ পাবে?

সমাধানঃ বছর শেষে লাভ হয় = 26500 টাকা

লভ্যাংশ থেকে বিনিয়োগ করা হয়=26500✕60%=15900 টাকা

অবশিষ্ট থাকে=(26500-15900) টাকা= 10600 টাকা।

খ হতে পাই,

অনুপাতের রাশিগুলোর যোগফল=53

∴আশিকের লভ্যাংশ=10600 এর (8/53) টাকা=1600 টাকা

এবং অহনার লভ্যাংশ=10600 এর (18/53) টাকা= 3600 টাকা।

∴অহনা লভ্যাংশ বেশি পায়=3600-1600 টাকা=2000 টাকা।

---

এসএসসি গণিত অনুশীলনী ১১.১

 এসএসসি সাধারণ গণিত সকল অধ্যায়