|
| ২০২২ সালের এসএসসি অ্যাসাইনমেন্ট ৯ম সপ্তাহ গণিত |
২০২২ সালের এসএসসি গণিত অ্যাসাইনমেন্ট ৯ম সপ্তাহ
বিষয়: কোড ১০৯
এসাইনমেন্ট নম্বর: ৩
অ্যাসাইনমেন্ট কাজঃ
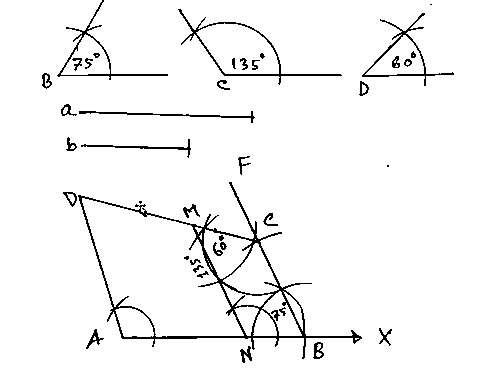
- পেন্সিল কম্পাস ব্যবহার করে 60⁰,75⁰ ও 135⁰ কোণ আঁক।
- তোমার আয়তাকার পড়ার টেবিলের দৈর্ঘ্য ও প্রস্থ পরিমাপ করে লিপিবদ্ধ করো।
শিখনফল/বিষয়বস্তুঃ
- প্রদত্ত উপাত্ত ব্যবহার করে চতুর্ভুজ ট্রাপিজিয়াম অঙ্কন করতে পারবে।
- প্রদত্ত উপাত্ত ব্যবহার করে ত্রিভুজ অঙ্কন করতে পারবে।
নির্দেশনাঃ
১। এখন একটি ট্রাপিজিয়াম আকৃতির টেবিলের উপরিতলের আনুপাতিক চিত্র আঁক যার সমান্তরাল বাহু দুইটি হবে তোমার আয়তাকার পড়ার টেবিলের দৈর্ঘ্য ও প্রস্থ এর সমান এবং ট্রাপিজিয়ামের ক্ষুদ্রতর টেবিলের প্রস্থ সংলগ্ন দুটি পণ্যের একটি হবে 75° এর সম্পূরক এবং অপরটি (135°) হবে। (পাঠ্যবইয়ের উদাহরণ ৩ (পৃষ্ঠা নম্বর- ১৪৭) সাহায্য নেবে প্রয়োজনে ক্ষুদ্রতর বাহুকে বর্ধিত করে বৃহত্তম বাহুর কেটে তার উপর একটি সামান্তরিক এঁকে চেষ্টা করবে)
২। ABCD একটি চতুর্ভুজের আনুপাতিক চিএ আঁক। যেখানে AB= টেবিলের প্রস্ত, (পাঠ্য বইয়ের অনুশীলনী ৭.২ এর ১১ নম্বর কে অনুসরণ করা যাবে)
৩। একটি ত্রিভুজ যার ভূমি তোমার টেবিলের প্রস্থ সমান ভূমি সংলগ্ন একটি কোণ 135° এবং অপর দুই বাহুর সমষ্টি তোমার টেবিলের দৈর্ঘ্য সমান। (পাঠ্যবইয়ের ১৩৮ পৃষ্ঠা সম্পাদ্য ১ অনুসরণ করবে)
 |
| ২০২২ সালের এসএসসি এসাইনমেন্ট নবম সপ্তাহ গণিত প্রশ্ন |
২০২২ সালের এসএসসি অ্যাসাইনমেন্ট ৯ম সপ্তাহ গণিত সমাধান
আজকের গণিত অ্যাসাইনমেন্ট ২০২২ সালের এসএসসি এর তিনটি প্রশ্ন রয়েছে তিনটি প্রশ্ন জ্যামিতি অংকন। তোমরা জ্যামিতি বক্স ব্যবহার করে সতর্কতার সাথে চিত্রগুলো অংকন করবে, কারণ তোমরা প্রশ্নে দেখছো রুব্রিকে বলা আছে চিত্র অংকন এর উপর অর্থাৎ সঠিক কোন অংকন এর উপর নম্বর বিভাজন রয়েছে।
১ নং প্রশ্নের উত্তর
👉 পেন্সিল কম্পাস ব্যবহার করে 60⁰,75⁰ ও 135⁰ কোণ আঙ্কনঃ
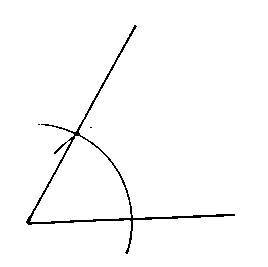 |
| চিত্রঃ 60⁰ কোণ |
 |
| চিত্রঃ 75⁰ কোণ |
 |
| চিত্রঃ 135⁰ কোণ |
আমার আয়তাকার পড়ার টেবিলের দৈর্ঘ্য হচ্ছে 3 ফুট এবং প্রস্থ হচ্ছে 2 ফুট। যা একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয় ধরে ট্রাপিজিয়াম আকৃতি টেবিলের আনুপাতিক চিত্র অঙ্কন করতে হবে যেখানে ট্রাপিজিয়ামের ক্ষুদ্রতম বাহু সংলগ্ন দুটি কোণের একটি হবে 75° এর সম্পূরক অর্থাৎ (180°-75°)=105° এবং অপরটি 135°।
অংকনঃ
মনে করি, টেবিলের দৈর্ঘ্য a এবং প্রস্থ b। আবার, ট্রাপিজিয়ামের ক্ষুদ্রতম বাহু সংলগ্ন কোণ 75° এর সম্পূরক অর্থাৎ (180°-75°)=105° এবং অপরটি 135° দেওয়া আছে। ট্রাপিজিয়ামটি আঁকতে হবে।
আমার টেবিলের প্রস্থ অর্থাৎ ট্রাপিজিয়ামের ক্ষুদ্রতম বাহু AE নিই। AE এর A বিন্দুতে 75° এর সমান করে ∠EAY অঙ্কন করি। AE কে B পর্যন্ত বর্ধিত করি যেন AB টেবিলের দৈর্ঘ্য a এর সমান হয়। B বিন্দুতে 45° এর সমান করে ∠ABZ অঙ্কন করি। E বিন্দুতে EC||AY আঁকি যা BZ রাশিকে C বিন্দুতে ছেদ করে। এবার CD||BA আঁকি। CD রেখাংশ AY কে D বিন্দুতে ছেদ করে। তাহলে ABCD ই ট্রাপিজিয়াম আকৃতি টেবিলের আনুপাতিক চিত্র,
প্রমাণঃ
ABCD ই ট্রাপিজিয়ামের ক্ষুদ্রতম বাহু CD সংলগ্ন দুটি কোনের একটি
∠ADC= ∠ADY-∠BAD
∠ADC= 180°-75°
∴ ∠ADC =105° যা 75° এর সম্পূরক
∠BCD= ∠BCZ-∠ABC
∠BCD= 180°-45°
২ নং প্রশ্নের উত্তর
বিশেষ নির্বচনঃ মনে করি একটি টেবিলের দৈর্ঘ্য AB ও টেবিলের প্রস্থ BC এবং ∠B=75°, ∠C=135° ও ∠D=60° কোণ দেওয়া আছে চতুর্ভুজটি আঁকতে হবে
অংকনঃ
যে কোনো রশ্মি.AX থেকে a এর সমান করে AB অংশ কেটে নিই। B বিন্দুতে ∠B=75° এর সমান করে ∠ABF আকি। BF থেকে b এর সমান করে BC কেটে নিই। C বিন্দুতে ∠C=135° এর সমান করে ∠BCD আকি। CD রশ্মির মধ্যে যে কোন একটি বিন্দু M নিই। M বিন্দুতে ∠D=60° এর সমান করে ∠CMNআঁকি। AD || MN আঁকি।
তাহলে ABCD ই উদ্দিষ্ট চতুর্ভুজ।