৫ম শ্রেণির গণিত ১৪ অধ্যায় সমাধান নিচে দেওয়া হলো। পঞ্চম শ্রেণির গণিত অনুশীলনী ১৪ ক্যালকুলেটর ও কম্পিউটার থেকে ছোট প্রশ্ন পরীক্ষায় এসে থাকে তাই এই অধ্যায়ের প্রস্তুতি গুরুত্বপূর্ণ।

৫ম শ্রেণির গণিত ১৪ অধ্যায় ক্যালকুলেটর ও কম্পিউটার

অনুশীলনী ১৪ প্রশ্ন ও সমাধান

১. একটি ক্যালকুলেটর ব্যবহার করে নিচের হিসাবগুলো কর :
(১) ১ × ২ × ৩ × ৪ × ৫ × ৬ × ৭ × ৮ × ৯ × ১০

(৩) ২.৪ ÷ {০.৩ × (৪০ × ০.১২৫ – ১)} – ২

(২) ১.১ × ১.১ × ১.১ × ১.১ × ১.১ × ১.১

(৪) (২.৩৫ × ৪.৯ – ০.১৫ × ৬.৩ + ২৭.৮৩) ÷ ১৫

সমাধান :

২. ক্যালকুলেটর ব্যবহার করে নিচের কাজগুলো কর :
(১) ক্যালকুলেটরের চার কোণা থেকে চারটি সংখ্যা নাও (১, ৩, ৭ ও ৯) এবং এই সংখ্যাগুলো দ্বারা শুরু হয় এরকম ৩ অঙ্ক বিশিষ্ট সংখ্যা ঘড়ির কাটার বিপরীত দিক অনুসারে (বাম হাতের দিক) ৪ বার নাও। যোগফল কত হবে?

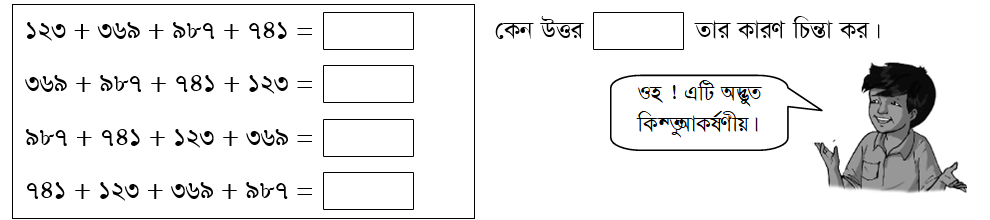
(২) (১, ২, ৩, ৪, ৫, ৬, ৭, ৮ ও ৯) থেকে যেকোনো সংখ্যা নাও এবং এই সংখ্যাগুলো দ্বারা শুরু হয় এরকম ৩ অঙ্ক বিশিষ্ট সংখ্যা ঘড়ির কাঁটার বিপরীত দিক অনুসারে (বাম হাতের দিক) অথবা ঘড়ির কাঁটার দিক অনুসারে (ডান হাতের দিক) ৪ বার নাও। যোগফল কত হবে? কেন উত্তর তার কারণ চিন্তা কর।
২১৪ + ৪৭৮ + ৮৯৬ + ৬৩২ =
৮৭৪ + ৪১২ + ২৩৬ + ৬৯৮ =

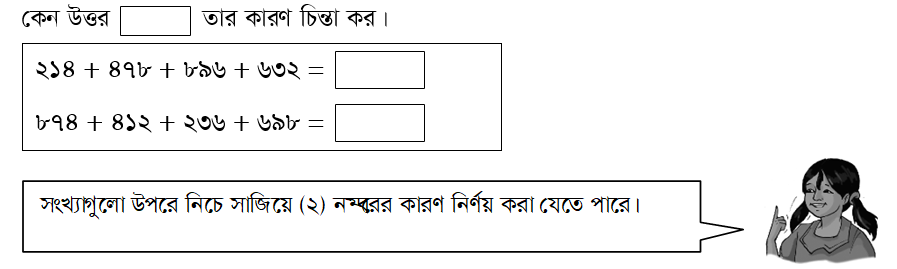
সমাধান :
(১)

কারণ : প্রতিটি যোগে পৃথকভাবে সংখ্যাগুলোর একক, দশক ও শতক স্থানীয় অঙ্কগুলো সমান। যেমন : প্রথম যোগে একক স্থানীয় অঙ্কগুলো হচ্ছে ৩, ৯, ৭, ১ ও দ্বিতীয় যোগে একক স্থানীয় অঙ্কগুলো হচ্ছে, ৯, ৭, ১, ৩। উভয়ক্ষেত্রেই অঙ্কগুলো সমান কিছু বিন্যাস বিভিন্ন তাই প্রতিটি যোগের যোগফল সমান।
(২) (১, ২, ৩, ৪, ৫, ৬, ৭, ৮ ও ৯) থেকে যেকোনো সংখ্যা নাও এবং এই সংখ্যাগুলো দ্বারা শুরু হয় এরকম ৩ অঙ্ক বিশিষ্ট সংখ্যা ঘড়ির কাঁটার বিপরীত দিক অনুসারে (বাম হাতের দিক) অথবা ঘড়ির কাঁটার দিক অনুসারে (ডান হাতের দিক) ৪ বার নাও। যোগফল কত হবে?

কেন উত্তর ২২২০ তার কারণ চিন্তা কর।

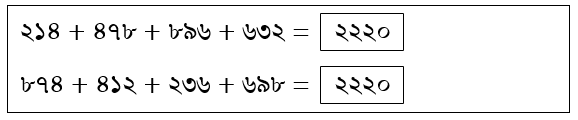
কারণ : (১) এর অনুরূপ।

🔶🔶 পঞ্চম শ্রেণির গণিত সকল অধ্যায়

🔶🔶 পঞ্চম শ্রেণির সকল বিষয়