চতুর্থ শ্রেণির গণিত অধ্যায় ১৪ ত্রিভুজ অনুশীলনী প্রশ্নোউত্তর সহ এই ১৪ অধ্যায় ত্রিভুজের সংক্ষিপ্ত ও সৃজনশীল প্রশ্ন ও উত্তর নিচে দেওয়া হলো।
চতুর্থ শ্রেণির গণিত অধ্যায় ১৪ ত্রিভুজ
১৪.২ অনুশীলনীর প্রশ্ন ও উত্তর
১। নিচের ত্রিভুজগুলো আঁক :
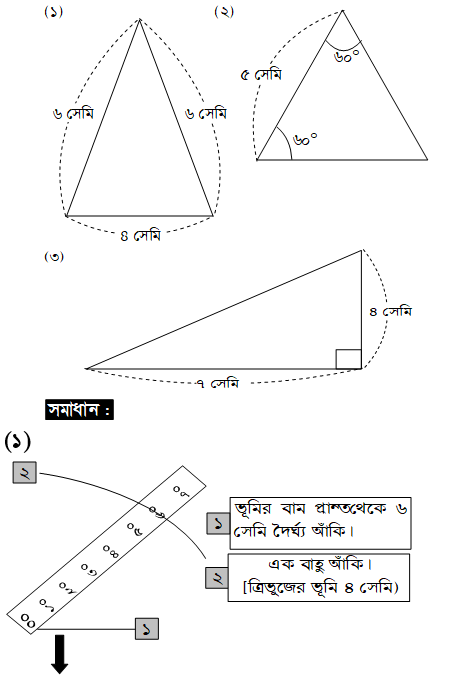


২। উপরের ত্রিভুজগুলোকে নিচের দুই ধরনের তালিকায় উল্লেখ কর :
| ত্রিভুজের ধরন | ত্রিভুজ (১) | ত্রিভুজ (২) | ত্রিভুজ (৩) |
| বাহু ভিত্তিতে | |||
| কোণ ভিত্তিতে |
সমাধানঃ
| ত্রিভুজের ধরন | ত্রিভুজ (১) | ত্রিভুজ (২) | ত্রিভুজ (৩) |
| বাহু ভিত্তিতে | সমদ্বিবাহু | সমবাহু | বিষমবাহু |
| কোণ ভিত্তিতে | সূক্ষকোণী | সূক্ষকোণী | সমকোণী |
৩। নিচের ত্রিভুজগুলোকে সমদলভুক্ত কর এবং ত্রিভুজগুলো দলভুক্তকরণের কারণ নিয়ে শ্রেণিতে আলোচনা কর।
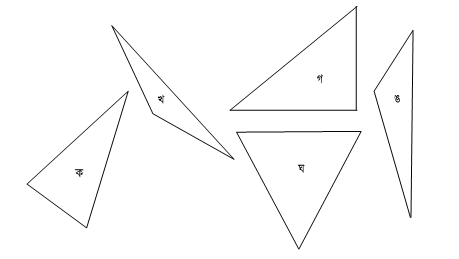
সমাধানঃ ত্রিভুজগুলোকে বাহুর ভিত্তিতে সমদলভুক্ত করে দলভুক্তকরণের কারণ আলোচনা করা হলো :
ক ও খ সমদ্বিবাহু ত্রিভুজ।
কারণ, ক ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য সমান অর্থাৎ ৪ সেমি। অপর বাহুর দৈর্ঘ্য ২.২ সেমি।
আবার খ ত্রিভুজেরও দুইটি বাহুর দৈর্ঘ্যরে পরিমাণ সমান অর্থাৎ ২.৮ সেমি এবং অপর বাহুর দৈর্ঘ্য ৫.৩ সেমি।
ক ও খ ত্রিভুজের প্রত্যেকটির দুইটি করে বাহু সমান।
গ ও ঙ বিষমবাহু ত্রিভুজ।
কারণ, গ ত্রিভুজের বাহুগুলোর দৈর্ঘ্য যথাক্রমে ৪.৮ সেমি, ৩.৮ সেমি ও ২.৯ সেমি যেগুলো পরস্পর অসমান।
আবার, ঙ ত্রিভুজের বাহুগুলোর দৈর্ঘ্য যথাক্রমে ৩.৬ সেমি, ৫.১ সেমি ও ২ সেমি যেগুলো পরস্পর অসমান।
গ ও ঙ ত্রিভুজের প্রত্যেকটির তিনটি বাহুর কোনোটিই সমান নয়।
ঘ সমবাহু ত্রিভুজ।
কারণ, প্রত্যেকটি বাহুর দৈর্ঘ্য ৩.৮ সেমি।
অর্থাৎ ঘ ত্রিভুজের প্রত্যেকটি বাহু সমান।
ত্রিভুজগুলোকে কোণের ভিত্তিতে সমদলভুক্ত করে দলভুক্তকরণের কারণ আলোচনা করা হলো :
ক ও ঘ সূক্ষকোণী ত্রিভুজ।
কারণ, ক ও ঘ এর সবগুলো কোণই ৯০° এর চেয়ে ছোট।
খ ও ঙ স্থূলকোণী ত্রিভুজ।
কারণ খ ও ঙ এর প্রত্যেকটির তিনটি কোণের একটি ৯০° এর চেয়ে বড়।
গ সমকোণী ত্রিভুজ।
কারণ গ এর একটি কোণ ৯০°।
৪র্থ শ্রেণির গণিত অধ্যায় ১৪ সংক্ষিপ্ত প্রশ্নের উত্তর
সাধারণ
১. ত্রিভুজ কাকে বলে?
উত্তর : তিনটি রেখাংশ দ্বারা আবদ্ধ চিত্রকে ত্রিভুজ বলে। ত্রিভুজের তিনটি বাহু ও তিনটি কোণ রয়েছে।
২. বাহুভেদে ত্রিভুজ কত প্রকার ও কী কী?
উত্তর : বাহুভেদে ত্রিভুজ তিন প্রকার : সমবাহু, সমদ্বিবাহু ও বিষমবাহু ত্রিভুজ।
৩. সমবাহু ত্রিভুজের সংজ্ঞা দাও।
উত্তর : যে ত্রিভুজের সবগুলো বাহু সমান তাকে সমবাহু ত্রিভুজ বলে।
৪. সমদ্বিবাহু ত্রিভুজ কাকে বলে?
উত্তর : যে ত্রিভুজের দুইটি বাহু সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে।
৫. বিষমবাহু ত্রিভুজ কাকে বলে?
উত্তর : যে ত্রিভুজের সবগুলো বাহু পরস্পর অসমান তাকে বিষমবাহু ত্রিভুজ বলে।
৬. কোণভেদে ত্রিভুজ কত প্রকার ও কী কী?
উত্তর : কোণভেদে ত্রিভুজ তিন প্রকার : সমকোণী, সূক্ষকোণী এবং স্থূলকোণী ত্রিভুজ।
৭. সমকোণী ত্রিভুজের সংজ্ঞা দাও।
উত্তর : যে ত্রিভুজের একটি কোণ সমকোণ (৯০°) তাকে সমকোণী ত্রিভুজ বলে।
৮. সূক্ষকোণী ত্রিভুজ কাকে বলে?
উত্তর : যে ত্রিভুজের তিনটি কোণই সূ²কোণ (৯০° এর ছোট) তাকে সূক্ষকোণী ত্রিভুজ বলে।
৯. স্থূলকোণী ত্রিভুজ কাকে বলে
উত্তর : যে ত্রিভুজের একটি কোণ স্থূলকোণ (৯০° এর বড়) তাকে স্থূলকোণী ত্রিভুজ বলে।
১০. ত্রিভুজের কয়টি বাহু থাকে?
উত্তর : ত্রিভুজের ৩টি বাহু থাকে।
১১. ত্রিভুজের কয়টি কোণ থাকে?
উত্তর : ত্রিভুজের ৩টি কোণ থাকে।
১২. ‘ত্রিভুজ’ শব্দের অর্থ কী?
উত্তর : ‘ত্রিভুজ’ শব্দের অর্থ তিন বাহু।
১৩. ত্রিভুজের বাহুগুলো কোথায় যুক্ত হয়?
উত্তর : ত্রিভুজের বাহুগুলো কৌণিক বিন্দুতে যুক্ত হয়।
১৪. তিন বাহু সমান থাকলে তাকে কী ত্রিভুজ বলে?
উত্তর : তিন বাহু সমান থাকলে তাকে সমবাহু ত্রিভুজ বলে।
১৫. তিন বাহু অসমান থাকলে তাকে কী ত্রিভুজ বলে?
উত্তর : তিন বাহু অসমান থাকলে তাকে বিষমবাহু ত্রিভুজ বলে।
১৬. ত্রিভুজের প্রত্যেকটি কোণ কয়টি বাহু মিলিত হয়ে গঠিত হয়?
উত্তর : ত্রিভুজের প্রত্যেকটি কোণ দুইটি বাহু মিলিত হয়ে গঠিত হয়।
যোগ্যতাভিত্তিক
১৭. কোন চিহ্ন দ্বারা ত্রিভুজ বোঝানো হয়?
উত্তর : ‘’ চিহ্নটি দ্বারা ত্রিভুজ বোঝানো হয়।
১৮. বিষমবাহু ত্রিভুজের চিত্র অঙ্কন কর।
উত্তর : 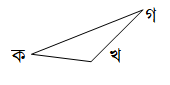
১৯.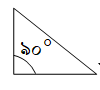 ত্রিভুজটির নাম কী?
ত্রিভুজটির নাম কী?
উত্তর : সমকোণী ত্রিভুজ।
২০. 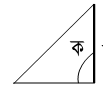 চিত্রের ক = ৯০° হলে ত্রিভুজটির নাম লেখ।
চিত্রের ক = ৯০° হলে ত্রিভুজটির নাম লেখ।
উত্তর : সমকোণী ত্রিভুজ।
২১.  চিত্রের ত্রিভুজটির নাম লেখ।
চিত্রের ত্রিভুজটির নাম লেখ।
উত্তর : বিষমবাহু ত্রিভুজ বা স্থূলকোণী ত্রিভুজ।
৪র্থ শ্রেণির গণিত অধ্যায় ১৪ কাঠামোবদ্ধ প্রশ্নের উত্তর (যোগ্যতাভিত্তিক)
১। নিচের উদ্দীপকটি লক্ষ কর এবং প্রশ্নগুলোর উত্তর দাও।
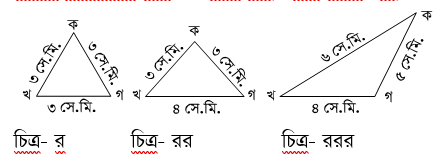
(ক) চিত্র- র, রর ও ররর এর নামগুলো লেখ। ২
(খ) চিত্র (র) এর ত্রিভুজের সংজ্ঞা দাও। ২
(গ) চিত্র (ররর) এর ত্রিভুজের সংজ্ঞা দাও। ২
(ঘ) চিত্র- রর ও চিত্র- ররর এর মধ্যে তুলনা কর। ২
(ঙ) চিত্র- র ও চিত্র- রর এর মধ্যে মিলগুলো কী কী? ২
সমাধানঃ
(ক) চিত্র- র এর নাম সমবাহু ত্রিভুজ।
চিত্র- রর এর নাম সমদ্বিবাহু ত্রিভুজ।
চিত্র- ররর এর নাম বিষমবাহু ত্রিভুজ।
(খ) চিত্র (র) এর ত্রিভুজটির প্রত্যেকটি বাহু ৩ সে.মি. বলে এটি সমবাহু ত্রিভুজ।
সমবাহু ত্রিভুজ : যে ত্রিভুজের তিনটি বাহু পরস্পর সমান তাকে সমবাহু ত্রিভুজ বলে।
(গ) চিত্র (ররর) এর ত্রিভুজটির বাহু তিনটি পরস্পর অসমান বলে এটি বিষমবাহু ত্রিভুজ।
বিষমবাহু ত্রিভুজ : যে ত্রিভুজের সবগুলো বাহু অসমান তাকে বিষমবাহু ত্রিভুজ বলে।
(ঘ) চিত্র- রর, একটি সমদ্বিবাহু ত্রিভুজ। এর দুইটি বাহু সমান, কোণগুলো সূ²কোণ।
চিত্র- ররর, একটি বিষমবাহু ত্রিভুজ। এর একটি কোণ স্থূলকোণ। অন্য দুইটি সূ²কোণ। এর কোনো বাহুই সমান নয়।
(ঙ) চিত্র- র ও চিত্র- রর এর প্রত্যেকটি কোণ সূ²কোণ। চিত্র- রর এর দুই বাহু ও চিত্র- ররর এর দুই বাহুর সমান।
২। 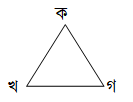
(ক) কখ = ৫ সেমি, খগ = ৩ সেমি ও কগ = ৫ সেমি পরিমাপ নিয়ে ত্রিভুজটি আঁক।
(খ) খগ = ৫ সেমি ও ∠ক = ∠খ = ৬০° হলে ত্রিভুজটি কী ধরনের এবং কেন?
(গ) খগ = ৮ সেমি এবং কগ = ৬ সেমি পরিমাপ নিয়ে ত্রিভুজ আঁক এবং কখ এর পরিমাপ নির্ণয় কর।
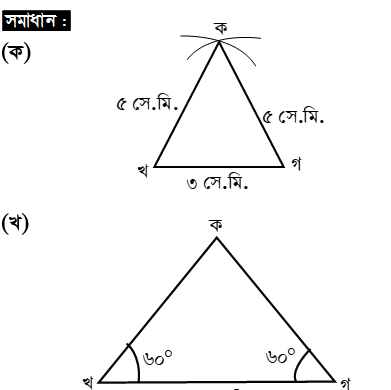
স্কেল ও চাঁদার সাহায্যে খগ = ৫ সেমি ও ∠খ = ৬০° ও ∠গ = ৬০° অঙ্কন করলাম। ফলে কখগ ত্রিভুজ পাওয়া গেল।
এখন স্কেলের সাহায্যে কখ = কগ = ৫ সেমি ও চাঁদার সাহায্যে ∠ক = ৬০° পাই। ফলে কখগ ত্রিভুজটি সমবাহু। কারণ কখ = কগ = খগ = ৫ সেমি এবং প্রত্যেকটি কোণ সমান অর্থাৎ ∠ক = ∠খ = ৬০°।
(গ)
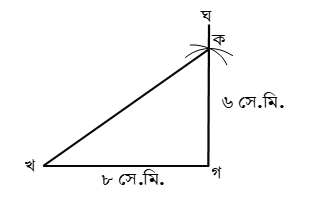
(১) স্কেলের সাহায্যে খগ = ৮ সেমি আঁকি।
(২) গ বিন্দুতে চাঁদার সাহায্যে ∠খগঘ = ৯০° কোণ আঁকি।
(৩) গঘ থেকে কগ = ৬ সেমি দৈর্ঘ্য আঁকি। স্কেলের সাহায্য কখ এর পরিমাপ ১০ সেমি পাই।