চতুর্থ শ্রেণির গণিত অধ্যায় ৭ গুণিতক ও গুণনীয়ক অনুশীলনী প্রশ্নোউত্তর সহ সংক্ষিপ্ত ও সৃজনশীল প্রশ্নোউত্তর দেওয়া হলো।

৪র্থ শ্রেণির গণিত ৭ম অধ্যায় গুণিতক ও গুণনীয়ক

গুরুত্বপূর্ণ তথ্য কিছু জেনে নেওয়া যাক।

◙ একটি সংখ্যা কোনো সংখ্যা দ্বারা বিভাজ্য হলে, প্রথমটিকে অন্যটির গুণিতক বলা হয়।
◙ একটি সংখ্যা কোনো সংখ্যা দ্বারা বিভাজ্য হলে, প্রথম সংখ্যাটি ভাজক ও ভাগফল প্রত্যেকের গুণিতক।
◙ প্রত্যেক সংখ্যা ১ এবং তার নিজেরও গুণিতক।
◙ প্রত্যেক সংখ্যার অসংখ্য গুণিতক রয়েছে।
◙ প্রত্যেক সংখ্যার ক্ষুদ্রতম গুণিতক সংখ্যাটি নিজেই।
◙ সবচেয়ে ছোট সাধারণ গুণিতকটিকে বলা হয় লঘিষ্ঠ সাধারণ গুণিতক (ল.সা.গু)।
◙ প্রত্যেক সংখ্যা নিজেই তার একটি গুণনীয়ক।
◙ ১ যেকোনো সংখ্যারই একটি গুণনীয়ক।
◙ দুইটি সংখ্যার সাধারণ গুণনীয়কগুলোর মধ্যে সবচেয়ে বড়টি গরিষ্ঠ সাধারণ গুণনীয়ক।
◙ দুইটি সংখ্যার গ.সা.গু ক্ষেত্রবিশেষে ১ হতে পারে।
◙ দুইটি সংখ্যার গ.সা.গু. ক্ষেত্রবিশেষে ছোট সংখ্যাটিও হতে পারে।
◙ একাধিক সংখ্যার সবচেয়ে বড় সাধারণ গুণনীয়কটিকে বলা হয় গরিষ্ঠ সাধারণ গুণনীয়ক (গ.সা.গু)।
◙ মৌলিক সংখ্যা : মৌলিক সংখ্যা হচ্ছে সকল সংখ্যা গঠনের মূল ভিত্তি। ১ এর চেয়ে বড় যেসব সংখ্যার ১ ও সংখ্যাটি ছাড়া অন্য কোনো গুণনীয়ক নেই, সেগুলো মৌলিক সংখ্যা। যেমন- ২, ৩, ৫ ইত্যাদি।
◙ যৌগিকসংখ্যা : ১ এর চেয়ে বড় যেসব সংখ্যার ১ ও সংখ্যাটি ছাড়া অন্তত একটি গুণনীয়ক আছে, সেগুলো যৌগিক সংখ্যা। যেমন- ১২ এর গুণনীয়ক ২, ৩, ৪, ৬। সুতরাং ১২ যৌগিক সংখ্যা।
◙ মৌলিক সংখ্যার গুণ দ্বারা যৌগিক সংখ্যা গঠন করা যায়।
◙ ১ মৌলিক সংখ্যা নয়, যৌগিক সংখ্যাও নয়।
◙ ২ ক্ষুদ্রতম মৌলিক সংখ্যা।
◙ ২ বাদে অন্যান্য মৌলিক সংখ্যা বিজোড় সংখ্যা। কিন্তু সকল বিজোড় সংখ্যা মৌলিক নয়। যেমন- ১৫ এর গুণনীয়ক ৩ ও ৫। সুতরাং ১৫ যৌগিক সংখ্যা।
◙ যৌগিক সংখ্যার গুণনীয়কের সংখ্যা কমপক্ষে তিনটি।
◙ কোনো সংখ্যা মৌলিক বা যৌগিক কি না নির্ণয়ের জন্য এমন সকল মৌলিক সংখ্যা দিয়ে সংখ্যাটির বিভাজ্যতা যাচাই করাই যথেষ্ট, যাদের বর্গ সংখ্যাটির চেয়ে বড় নয়।
◙ জোড় সংখ্যা ২ দ্বারা বিভাজ্য হবে। যেমন- ৪, ৬ ও ৮, ২ দ্বারা বিভাজ্য।
◙ কোনো সংখ্যার অঙ্কগুলোর সমষ্টি ৩ দ্বারা বিভাজ্য হলে, সংখ্যাটি ৩ দ্বারা বিভাজ্য হবে। যেমন- ৬৭২ এর অঙ্কগুলোর সমষ্টি ৬ + ৭ + ২ = ১৫, ৩ দ্বারা বিভাজ্য। সুতরাং ৬৭২, ৩ দ্বারা বিভাজ্য।
◙ কোনো সংখ্যার একক স্থানীয় অঙ্ক ০ বা ৫ হলে, সংখ্যাটি ৫ দ্বারা বিভাজ্য হবে। যেমন- ১০, ১৫, ২০ দ্বারা বিভাজ্য।

 

৭.৪ অনুশীলনীর প্রশ্ন ও উত্তর

১। নিচের সংখ্যাগুলোর ৩টি গুণিতক লিখে ছোট থেকে বড় ক্রমে সাজাও :
(১) ৪ (২) ৭ (৩) ১১ (৪) ১৪

নিয়মঃ প্রদত্ত সংখ্যাটিকে ধারাবাহিকভাবে ১, ২, ৩ ….. দ্বারা গুণ করে সংখ্যাটির একাধিক গুণিতক নির্ণয় করা যায়।
(১) ৪

সমাধানঃ

৪ × ১ = ৪    ৪ × ২ = ৮      ৪ × ৩ = ১২
ছোট থেকে বড় ক্রমে ৪ এর তিনটি গুণিতক : ৪, ৮, ১২
উত্তর : ৪, ৮, ১২।
(২) ৭
সমাধানঃ
৭ × ১ = ৭ ৭ × ২ = ১৪ ৭ × ৩ = ২১
ছোট থেকে বড় ক্রমে ৭ এর তিনটি গুণিতক : ৭, ১৪, ২১
উত্তর : ৭, ১৪, ২১।
(৩) ১১

সমাধানঃ
১১ × ১ = ১১ ১১ × ২ = ২২
১১ × ৩ = ৩৩
ছোট থেকে বড় ক্রমে ১১ এর তিনটি গুণিতক : ১১, ২২, ৩৩
উত্তর : ১১, ২২, ৩৩।

(৪) ১৪

সমাধানঃ
১৪ × ১ = ১৪ ১৪ × ২ = ২৮
১৪ × ৩ = ৪২
ছোট থেকে বড় ক্রমে ১৪ এর তিনটি গুণিতক : ১৪, ২৮, ৪২
উত্তর : ১৪, ২৮, ৪২।

২। নিচের সংখ্যার জোড়গুলোর জন্য ৩টি সাধারণ গুণিতক লিখে ছোট থেকে বড় ক্রমে সাজাও। লঘিষ্ঠ সাধারণ গুণিতকটি (লসাগু) লেখ :
(১) ৩, ৪ (২) ৪, ৯ (৩) ৩, ৯ (৪) ৫, ৮

(১) ৩, ৪
সমাধানঃ

ছোট থেকে বড় ক্রমে ৩ ও ৪ এর তিনটি সাধারণ গুণিতক হলো ১২, ২৪, ৩৬।
এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতক হলো ১২।
∴ ৩ ও ৪ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ১২।
উত্তর : ১২, ২৪, ৩৬; লসাগু: ১২।

(২) ৪, ৯

সমাধানঃ

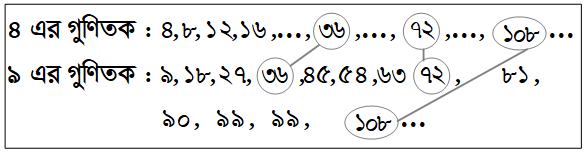
ছোট থেকে বড় ক্রমে ৪ ও ৯ এর তিনটি সাধারণ গুণিতক হলো ৩৬, ৭২, ১০৮। এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতক ৩৬
∴ ৪ ও ৯ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ৩৬
উত্তর : ৩৬, ৭২, ১০৮; লসাগু: ৩৬।

(৩) ৩, ৯

সমাধানঃ

ছোট থেকে বড় ক্রমে ৩ ও ৯ এর তিনটি সাধারণ গুণিতক হলো ৯, ১৮, ২৭। এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ৯
∴ ৩ ও ৯ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ৯
উত্তর : ৯, ১৮, ২৭; লসাগু: ৯।

(৪) ৫, ৮
সমাধানঃ

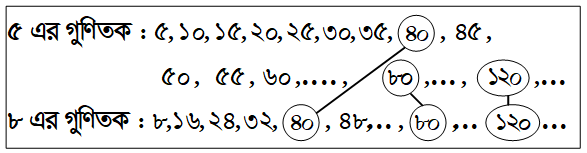
ছোট থেকে বড় ক্রমে ৫ ও ৮ এর তিনটি সাধারণ গুণিতক হলো ৪০, ৮০, ১২০। এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ৪০।
∴ ৫ ও ৮ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ৪০।
উত্তর : ৪০, ৮০, ১২০; লসাগু: ৪০।

৩। নিচের সংখ্যাগুলোর সকল গুণনীয়ক লেখ :
(১) ৯ (২) ১২ (৩) ২৪ (৪) ৩০

(১) ৯

সমাধানঃ

৯ = ১ × ৯
= ৩ × ৩
৯ এর গুণনীয়ক : ১, ৩, ৯
উত্তর : ১, ৩, ৯।

(২) ১২

সমাধানঃ
১২ = ১ × ১২
= ২ × ৬
= ৩ × ৪
১২ এর গুণনীয়ক : ১, ২, ৩, ৪, ৬, ১২।
উত্তর : ১, ২, ৩, ৪, ৬, ১২।

(৩) ২৪

সমাধানঃ
২৪ = ১ × ২৪
= ২ × ১২
= ৩ × ৮
= ৪ × ৬
২৪ এর গুণনীয়ক : ১, ২, ৩, ৪, ৬, ৮, ১২, ২৪।
উত্তর : ১, ২, ৩, ৪, ৬, ৮, ১২, ২৪।

(৪) ৩০

সমাধানঃ
৩০ = ১ × ৩০
= ২ × ১৫
= ৩ × ১০
= ৫ × ৬
৩০ এর গুণনীয়ক : ১, ২, ৩, ৫, ৬, ১০, ১৫, ৩০।
উত্তর : ১, ২, ৩, ৫, ৬, ১০, ১৫, ৩০।

৪। নিচের সংখ্যাগুলোর সকল সাধারণ গুণনীয়ক নির্ণয় কর এবং প্রতিটি সংখ্যাযুগলের গরিষ্ঠ সাধারণ গুণনীয়কটি (গসাগু) লেখ :
(১) ৯, ১৫ (২) ১৪, ২১ (৩) ২৪, ৪০ (৪) ৫, ৯

(১) ৯, ১৫

সমাধানঃ

৯ এর গুণনীয়ক : ১, ৩, ৯
১৫ এর গুণনীয়ক : ১,৩ , ৫, ১৫

৯ ও ১৫ এর সাধারণ গুণনীয়কগুলো হলো ১ ও ৩। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়ক হলো ৩।
∴ ৯ ও ১৫ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) হলো ৩।
উত্তর : ১, ৩; গসাগু: ৩।

(২) ১৪, ২১

সমাধানঃ

১৪ এর গুণনীয়ক :১ , ২, ৭, ১৪
২১ এর গুণনীয়ক :১ , ৩,৭ , ২১

১৪ ও ২১ এর সাধারণ গুণনীয়কগুলো হলো ১ ও ৭। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়ক হলো ৭।
∴ ১৪ ও ২১ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) হলো ৭।
উত্তর : ১, ৭; গসাগু: ৭।

(৩) ২৪, ৪০

সমাধানঃ

২৪ ও ৪০ এর সাধারণ গুণনীয়কগুলো হলো ১, ২, ৪, ৮ এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়ক হলো ৮।
∴ ২৪ ও ৪০ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) হলো ৮।
উত্তর : ১, ২, ৪, ৮; গসাগু: ৮।

(৪) ৫, ৯

সমাধানঃ
৫ এর গুণনীয়ক : ১, ৫
৯ এর গুণনীয়ক :১ , ৩, ৩

৫ ও ৯ এর মধ্যে একমাত্র সাধারণ গুণনীয়কটি হলো ১।
∴ ৫ ও ৯ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) হলো ১।
উত্তর : ১; গসাগু: ১।

৫। লঘিষ্ঠ সাধারণ গুণিতক (লসাগু) ও গরিষ্ঠ সাধারণ গুণনীয়ক (গসাগু) নির্ণয় কর :
(১) ৮, ১২, ২৪ (২) ৯, ১২, ১৮

(১) ৮, ১২, ২৪

সমাধানঃ

৮, ১২, ও ২৪ এর সাধারণ গুণিতকগুলো হলো ২৪, ৪৮, ৭২ এবং আরও অনেক সংখ্যা, এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ২৪।
∴ ৮, ১২, ও ২৪ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ২৪।
আবার

৮, ১২, ২৪ এর সাধারণ গুণনীয়কগুলো হলো ১, ২, ৪। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়কটি হলো ৪
∴ ৮, ১২, ও ২৪ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গসাগু) হলো ৪
উত্তর : লসাগু: ২৪, গসাগু:৪

(২) ৯, ১২, ১৮
সমাধানঃ

৯, ১২ ও ১৮ এর সাধারণ গুণিতকগুলো হলো ৩৬, ৭২, ১০৮ এবং আরও অনেক সংখ্যা। এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ৩৬।
∴ ৯, ১২ ও ১৮ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ৩৬।
আবার,

৯, ১২ ও ১৮ এর সাধারণ গুণনিয়কগুলো হলো ১ ও ৩। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়কটি হলো ৩।
∴ ৯, ১২ ও ১৮ এর গরিষ্ঠ সাধারণ গুণণিয়কটি (গ সা গু) হলো ৩।
উত্তর : লসাগু: ৩৬, গসাগু: ৩।

৬। যেকেনো যৌগিক সংখ্যা তৈরির জন্য খালি ঘরে ২, ৩, ও ৫ সংখ্যা বসাও :
(১) ⬜ × ⬜ × ⬜ = ⬜
(২) ⬜ × ⬜ × ⬜ × ⬜ = ⬜
(৩) ⬜ × ⬜ × ⬜ × ⬜ = ⬜

সমাধানঃ

৭। বক্সের সংখ্যাগুলোর মধ্য থেকে ২, ৩ ও ৫ এর গুণিতক নির্ণয় কর :
২৪৮, ৩৩৯, ১২১, ৫১৫,
৪৬০, ৯১২, ৭৫১, ৫৫৫,
৮১০, ৯৫১, ১৩১, ৭২৫

সমাধানঃ

(১) ২ এর গুণিতক [২৪৮, ৪৬০, ৮১০, ৯১২]
(২) ৩ এর গুণিতক [৩৩৯, ৫৫৫, ৮১০, ৯১২, ৯৫১]
(৩) ৫ এর গুণিতক [৪৬০, ৫১৫, ৫৫৫, ৭২৫, ৮১০]

৮। দুইটি ঘণ্টার মধ্যে ক ঘণ্টাটি প্রতি ৮ মিনিট অন্তর এবং খ ঘণ্টাটি প্রতি ৬ মিনিট অন্তর বাজে। ঘণ্টা দুইটি দুপুর ১২টায় একত্রে বাজে। পরবর্তী কোন সময়ে ঘণ্টা দুইটি একত্রে বাজবে?

সমাধানঃ

৮ ও ৬ এর ল সা গু যত, তত মিনিট পর ক ও খ ঘণ্টা দুইটি একত্রে বাজবে।

৮ ও ৬ এর সাধারণ গুণিতকগুলো হলো ২৪, ৪৮ এবং আরও অনেক সংখ্যা। এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ২৪।
∴ ৮ ও ৬ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ২৪।
∴ ক ও খ ঘণ্টা দুইটি একত্রে বাজবে (দুপুর ১২টা + ২৪ মি)
= দুপুর ১২টা ২৪ মি)
অতএব পরবর্তী দুপুর ১২টা ২৪ মিনিটে ঘণ্টা দুইটি একত্রে বাজবে।
উত্তর : দুপুর ১২টা ২৪ মিনিটে।

৯। আমার কাছে ৩৬ সেমি লম্বা ও ২৪ সেমি চওড়া একটি কাগজ আছে। আমি একই আকৃতির বর্গ দিয়ে কাগজের পৃষ্ঠাটি ঢাকতে চাই। সম্ভাব্য সবচেয়ে বড় কাগজের বর্গটির বাহুর দৈর্ঘ্য কত?

সমাধানঃ

৩৬ ও ২৪ এর গসাগু-ই হবে নির্ণেয় সম্ভাব্য সবচেয়ে বড় বর্গটির বাহুর দৈর্ঘ্য।

৩৬ ও ২৪ এর সাধারণ গুণনীয়কগুলো হলো ১, ২, ৩, ৪, ৬, ১২। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়কটি হলো ১২।
∴ ৩৬ ও ২৪ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) হলো ১২।
সুতরাং সম্ভাব্য সবচেয়ে বড় বর্গটির বাহুর দৈর্ঘ্য ১২ সেমি।
উত্তর : ১২ সেমি।

১০। ৭ সেমি লম্বা ও ৫ সেমি চওড়া আয়তাকার টালিকে সাজিয়ে পাশে দেখানো ছবির মত একটি ক্ষুদ্রতম বাহুবিশিষ্ট বর্গ তৈরি করতে চাইলে কত সেন্টিমিটার বাহুবিশিষ্ট ক্ষুদ্রতম বর্গ তৈরি করা যাবে?

সমাধানঃ

৭ ও ৫ এর ল সা গু যত, তত সেমি হবে ক্ষুদ্রতম বর্গের বাহুর দৈর্ঘ্য।

৭ ও ৫ এর সাধারণ গুণিতকগুলো হলো ৩৫, ১০৫ ও আরও অনেক সংখ্যা এদের মধ্যে সবচেয়ে ছোট সাধারণ গুণিতকটি হলো ৩৫।
∴ ৭ ও ৫ এর লঘিষ্ঠ সাধারণ গুণিতকটি (ল সা গু) হলো ৩৫।
সুতরাং ৩৫ সেমি বাহুবিশিষ্ট ক্ষুদ্রতম বর্গ তৈরি করা যাবে।
উত্তর : ৩৫ সেমি।

১১। রাসেলের কাছে ৪৫টি আপেল ও ১৮টি কমলা আছে। রাসেল কোনো আপেল বা কমলা অবশিষ্ট না রেখে যত বেশি সম্ভব শিশুর মধ্যে এমনভাবে ভাগ করে দিতে চায় যাতে প্রত্যেকে সমান সংখ্যক আপেল ও কমলা পায়। রাসেল কত জন শিশুর মাঝে এগুলো ভাগ করে দিতে পারবে এবং প্রত্যেক শিশু কতটি করে আপেল ও কমলা পাবে?

সমাধানঃ

৪৫ ও ১৮ এর গসাগু ই নির্ণেয় বেশি সংখ্যক শিশুর সংখ্যা।

৪৫ ও ১৮ এর সাধারণ গুণনীয়কগুলো হলো ১, ৩, ৯। এদের মধ্যে সবচেয়ে বড় সাধারণ গুণনীয়কটি হলো ৯।
∴ ৪৫ ও ১৮ এর গরিষ্ঠ সাধারণ গুণনীয়কটি (গ সা গু) ৯
সুতরাং রাসেল ৯ জন শিশুর মাঝে আপেল ও কমলাগুলো ভাগ করে দিতে পারবে।
∴প্রত্যেক শিশু আপেল পাবে (৪৫ ÷ ৯) টি বা ৫টি এবং প্রত্যেক শিশু কমলা পাবে (১৮ ÷ ৯) টি বা ২টি।
উত্তর : ৯ জন; ৫টি আপেল, ২টি কমলা।

৪র্থ শ্রেণির গণিত ৭ম অধ্যায় সংক্ষিপ্ত প্রশ্নোত্তর

 সাধারণ
১. গুণনীয়ক কাকে বলে?
উত্তর : কোনো সংখ্যা যে যে সংখ্যা দ্বারা বিভাজ্য, সেগুলোই ঐ সংখ্যার গুণনীয়ক।
২. গুণনীয়কের অপর নাম কী?
উত্তর : গুণনীয়কের অপর নাম উৎপাদক।
৩. কোনো সংখ্যার দুটি সাধারণ গুণনীয়ক কী কী?
উত্তর : সংখ্যাটি নিজেই এবং ১।
৪. মৌলিক সংখ্যা কাকে বলে?
উত্তর : ১ এর চেয়ে বড় যেসব সংখ্যার ১ এবং সংখ্যাটি ছাড়া অন্য কোনো গুণনীয়ক নেই, সেগুলো মৌলিক সংখ্যা।
৫. যৌগিক সংখ্যা কী?
উত্তর : ১ এর চেয়ে বড় যেসব সংখ্যার ১ এবং সংখ্যাটি ছাড়া অন্তত একটি গুণনীয়ক আছে, সেগুলো যৌগিক সংখ্যা।
৬. ক্ষুদ্রতম মৌলিক সংখ্যা কোনটি?
উত্তর : ক্ষুদ্রতম মৌলিক সংখ্যা হচ্ছে ২।
৭. একমাত্র জোড় মৌলিক সংখ্যা কোনটি?
উত্তর : একমাত্র জোড় মৌলিক সংখ্যা হচ্ছে ২।
৮. যৌগিক সংখ্যার কমপক্ষে কয়টি উৎপাদক থাকে?
উত্তর : যৌগিক সংখ্যার কমপক্ষে তিনটি উৎপাদক থাকে।
৯. কোনো সংখ্যা তিন দ্বারা বিভাজ্য; এটি পরীক্ষার উপায় কী?
উত্তর : কোনো সংখ্যার অঙ্কগুলোর সমষ্টি ৩ দ্বারা বিভাজ্য হলে, সংখ্যাটি ৩ দ্বারা বিভাজ্য হবে।
১০. ৫ দ্বারা বিভাজ্যতার পরীক্ষার উপায় কী?
উত্তর : কোনো সংখ্যার একক স্থানীয় অঙ্ক ০ বা ৫ হলে, সংখ্যাটি ৫ দ্বারা বিভাজ্য হবে।
১১. গ.সা.গু. কাকে বলে?
উত্তর : দুইটি সংখ্যার সাধারণ গুণনীয়কগুলোর মধ্যে সবচেয়ে বড়টি গরিষ্ঠ সাধারণ গুণনীয়ক (গ.সা.গু.)।
১২. গ.সা.গু. এর দুটি বিশেষ ক্ষেত্র কী কী?
উত্তর :
১. দুইটি সংখ্যার গ.সা.গু. ক্ষেত্রবিশেষে ১ হতে পারে।
২. দুইটি সংখ্যার গু.সা.গু. ক্ষেত্রবিশেষে ছোটটিও হতে পারে।
১৩. গুণিতক কাকে বলে?
উত্তর : একটি সংখ্যা কোনো সংখ্যা দ্বারা বিভাজ্য হলে, প্রথমটিকে অন্যটির গুণিতক বলা হয়।
১৪. কোনো সংখ্যার গুণিতক সংখ্যা কতটি?
উত্তর : কোনো সংখ্যার গুণিতক সংখ্যা অসংখ্য।
১৫. ল.সা.গু. কাকে বলে?
উত্তর : কতগুলো সংখ্যার সাধারণ গুণিতকগুলোর মধ্যে সবচেয়ে ছোটটিকে লঘিষ্ঠ সাধারণ গুণিতক বা ল.সা.গু. বলে।
 যোগ্যতাভিত্তিক
১৬. ২ অঙ্কটির দুটি উৎপাদক লেখ।
উত্তর : ১ ও ২
১৭. ০, ১, ২, ৩, ৫ ও ৭ এর মধ্যে ক্ষুদ্রতম মৌলিক সংখ্যা কোনটি?
উত্তর : ২
১৮. ২৪ সংখ্যাটি ৩ দ্বারা বিভাজ্য; এটি পরীক্ষা করা যায় কিভাবে?
উত্তর : ২৪ এর অঙ্ক ২ ও ৪ যোগ করে ৩ দ্বারা ভাগের মাধ্যমে বিভাজ্যতা পরীক্ষা করা যায়।
১৯. ১ মৌলিক না যৌগিক সংখ্যা?
উত্তর : ১ মৌলিক সংখ্যা নয়, যৌগিক সংখ্যাও নয়।
২০. ২, ৪, ৬ এর ল.সা.গু. ও গ.সা.গু. কত?
উত্তর : ল.সা.গু. ১২ এবং গ.সা.গু. ২।
২১. ১০০ ও ১২৫ সংখ্যা দুটি ৫ দ্বারা বিভাজ্য হবে, এটি কিভাবে বোঝা যাবে?
উত্তর : ১০০ ও ১২৫ সংখ্যা দুটির একক স্থানে ০ ও ৫ আছে। তাই সংখ্যা দুটি ৫ দ্বারা বিভাজ্য হবে।
২২. মৌলিক সংখ্যার পাঁচটি উদাহরণ লেখ ।
উত্তর : ২, ৩, ৫, ৭ ও ১১ মৌলিক সংখ্যা।
২৩. ৩টি যৌগিক সংখ্যার উদাহরণ দাও।
উত্তর : ৮, ১৬ ও ২০।

চতুর্থ শ্রেণির গণিত সপ্তম অধ্যায় কাঠামোবদ্ধ প্রশ্নোত্তর (যোগ্যতাভিত্তিক)

১। নিচের উদ্দীপকটি লক্ষ কর এবং প্রশ্নগুলোর উত্তর দাও।
১৮, ২৪ ও ৩৬ দুই অঙ্ক বিশিষ্ট তিনটি সংখ্যা।
ক. উৎপাদক কাকে বলে? ২
খ. উদ্দীপকের ১ম দুটি সংখ্যার গ.সা.গু বের কর। ২
গ. উদ্দীপকের শেষের দুটি সংখ্যার ল.সা.গু. কত? ২
ঘ. সংখ্যাগুলোকে ৩ দ্বারা বিভাজ্যতা পরীক্ষা কর। ২
সমাধান:
ক. কোনো সংখ্যা যে যে সংখ্যা দ্বারা বিভাজ্য, সেগুলোই ঐ সংখ্যার গুণনীয়ক। গুণনীয়ককে উৎপাদকও বলা হয়।
খ. ১৮ এর সকল গুণনীয়ক ১, ২, ৩, ৬, ৯, ১৮।
২৪ এর সকল গুণনীয়ক ১, ২, ৩, ৪, ৬, ৮, ১২, ২৪।
∴ ১৮ ও ২৪ এর সাধারণ গুণনীয়কগুলো ১, ২, ৩, ৬। গুণনীয়কগুলোর মধ্যে ৬ সবচেয়ে বড়।
নির্ণেয় গ.সা.গু = ৬।
গ. ১৮ এর গুণিতক : ১৮, ৩৬, ৫৪, ৭২
২৪ এর গুণিতক : ২৪, ৪৮, ৭২
১৮ ও ২৪ এর সবচেয়ে ছোট সাধারণ গুণিতক হলো ৭২।
নির্ণেয় ল.সা.গু = ৭২।
ঘ. ১ + ৮ = ৯ ÷ ৩ = ৩; ∴ ১৮, ৩ দ্বারা বিভাজ্য।
২ + ৪ = ৬ ÷ ৩ = ২; ∴ ২৪, ৩ দ্বারা বিভাজ্য।
৩ + ৬ = ৯ ÷ ৩ = ৩; ∴ ৩৬, ৩ দ্বারা বিভাজ্য।

২। নিচের উদ্দীপকটি লক্ষ কর এবং প্রশ্নগুলোর উত্তর দাও।
১৫, ৩০, ৪৫ ও ৬০ চারটি দুই অঙ্কবিশিষ্ট সংখ্যা।
ক. ১৫ ও ৩০ এর গুণনীয়ক নির্ণয় কর। ২
খ. ১৫ ও ৩০ এর গ.সা.গু নির্ণয় কর। ২
গ. ১৩ ও ৩০ এর ল.সা.গু নির্ণয় কর। ২
ঘ. সংখ্যাগুলোকে ৩ দ্বারা বিভাজ্যতা পরীক্ষা কর। ২
সমাধান:
ক. ১৫ = ১ × ১৫
= ৩ × ৫
১৫ এর সকাল গুণনীয়ক ১, ৩, ৫, ১৫
৩০ = ১ × ৩০
= ২ × ১৫
= ৩ × ১০
= ৫ × ৬
৩০ এর সকল গুণনীয়ক ১, ২, ৩, ৫, ৬, ১০, ১৫, ৩০।
খ. ১৫ এর সকল গুণনীয়ক ১, ৩, ৫, ১৫
৩০ এর সকল গুণনীয়ক ১, ২, ৩, ৫, ৬, ১০, ১৫
১৫ ও ৩০ এর সাধারণ গুণনীয়ক ১, ৩, ৫, ১৫।
এদের মধ্যে সবচেয়ে বড় ১৫।
নির্ণেয় গ.সা.গু. ১৫।
গ. ১৫ এর গুণিতক : ১৫, ৩০, ৪৫, ৬০,…..
৩০ এর গুণিতক : ৩০, ৬০,…..
১৫ ও ৩০ এর সবচেয়ে ছোট সাধারণ গুণিতক হলো ৩০।
নির্ণেয় ল.সা.গু. = ৩০।
ঘ. ১ + ৫ = ৬ ÷ ৩ = ২, ১৫; ৩ দ্বারা বিভাজ্য।
৩ + ০ = ৩ ÷ ৩ = ১, ৩০, ৩ দ্বারা বিভাজ্য।
৪ + ৫ = ৯ ÷ ৩ = ৩, ৪৫, ৩ দ্বারা বিভাজ্য।
৬ + ০ = ৬ ÷ ৩ = ২, ৬০, ৩ দ্বারা বিভাজ্য।