নবম দশম শ্রেণির বা এসএসসি গণিত অনুশীলনী ১২.৩ প্রশ্ন সমাধান নিচে দেওয়া হলো।
নবম-দশম গণিত অনুশীলনী ১২.৩ প্রশ্ন সমাধান
বি.দ্র: কিছু ফন্ট ঠিক দেখতে Google Chrome Browser ব্যবহার করুন।
লেখচিত্রের সাহায্যে সমাধান কর :
প্রশ্ন \ 1 \ 3x + 4y = 14
4x – 3y = 2
সমাধান : প্রদত্ত সমীকরণদ্বয়,
3x + 4y = 14…………………. (i)
4x – 3y = 2 …………………. (ii)
সমীকরণ (i) থেকে পাই,
4y = 14 – 3x
বা, y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 0 | 2 |
| y | 5 | 2 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (-2, 5), , (2, 2)
আবার সমীকরণ (ii) থেকে পাই,
– 3y = 2 – 4x
বা, 3y = 4x – 2
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | -1 | 0 | 5 |
| y | -2 | 6 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (-1, – 2), , (5, 6)|
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং o মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গের প্রতি দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন (i)নং সমীকরণের (-2, 5), , (2, 2) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। আবার, (ii) নং সমীকরণের (-1, – 2),
, (5, 6) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে।

লেখ থেকে দেখা যায় A বিন্দুর স্থানাঙ্ক A(2, 2) যা উভয় সমীকরণকে সিদ্ধ করে।
∴ সমাধান : (x, y) = (2, 2)
প্রশ্ন \ 2 \ 2x – y = 1
5x + y = 13
সমাধান : প্রদত্ত সমীকরণদ্বয়,
2x – y = 1 …………….. (i)
5x + y = 13 …………… (ii)
সমীকরণ (1) থেকে পাই, – y = 1 – 2x
বা, y = 2x – 1
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 2 | 4 |
| y | -1 | 3 | 7 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, -1), (2, 3), (4, 7)
আবার, (ii) নং সমীকরণ থেকে পাই, y = 13 – 5x
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 2 | 3 |
| y | 13 | 3 | -2 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 13), (2, 3), (3, -2)|
মনে করি, XOX’ ও YOY’ যথাক্রমে x অক্ষ ও y অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের এক বাহুর দৈর্ঘ্যকে একক ধরি। এখন, (i) নং সমীকরণের (0, -1), (2, 3), (4, 7) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এটি 2x – y = 3 সমীকরণের লেখ।
আবার, (ii) নং সমীকরণের (0, 13), (2, 3), (3, -2)| বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি। ফলে একটি সরলরেখা পাওয়া গেছে এটি 5x + y = 13 সমীকরণের লেখ। সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে।
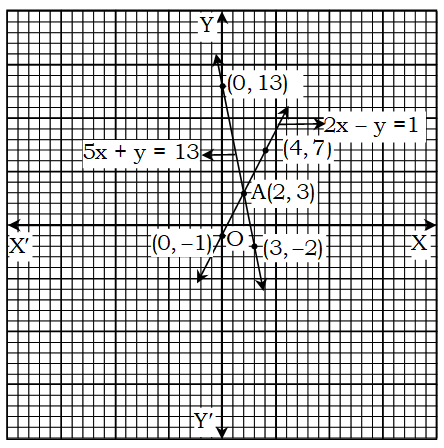
লেখ থেকে দেখা যায় A বিন্দুর স্থানাঙ্ক A(2, 3) যা উভয় সমীকরণকে সিদ্ধ করে।
∴ সমাধান: (x, y) = (2, 3)
প্রশ্ন \ 3 \ 2x + 5y = 1
x + 3y = 2
সমাধান : প্রদত্ত সমীকরণদ্বয়,
2x + 5y = 1 ………………. (i)
x + 3y = 2 ………………… (ii)
সমীকরণ (i) থেকে পাই,
5y = 1 – 2x
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 0 | 3 |
| y | 1 | -1 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (- 2, 1), , (3, -1)|
আবার, সমীকরণ (ii) থেকে পাই,
3y = 2 – x
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | -1 | 2 | 5 |
| y | 1 | 0 | -1 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (-1, 1), (2, 0), (5, -1)|
মনে করি, XOX’ ও YOY’ যথাক্রমে x অক্ষ ও y অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন (i) নং সমীকরণের (- 2, 1), , (3, -1)| বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এটিই 2x + 5y = 1 সমীকরণের লেখ।
আবার, (ii) নং সমীকরণের (-1, 1), (2, 0), (5, -1)| বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি প্রাপ্ত সরলরেখা দুটি পরস্পর A বিন্দুতে ছেদ করে।

লেখ থেকে দেখা যায়, A বিন্দুর স্থানাঙ্ক A(-7, 3) যা উভয় সমীকরণকে সিদ্ধ করে।
∴ সমাধান : (x, y) = (-7, 3)
প্রশ্ন \ 4 \ 3x – 2y = 2
5x – 3y = 5
সমাধান : প্রদত্ত সমীকরণদ্বয়,
3x – 2y = 2……………… (i)
5x – 3y = 5……………… (ii)
সমীকরণ (i) থেকে পাই,
– 2y = 2 – 3x
বা, 2y = 3x – 2
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 0 | 4 |
| y | – 4 | -1 | 5 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (-2,-4), (0, -1), (4, 5)
আবার, সমীকরণ (ii) থেকে পাই,
– 3y = 5 – 5x
বা, 3y = 5x – 5
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 1 | 4 |
| y | – 5 | 0 | 5 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (- 2, – 5),(1, 0), (4, 5)
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন সমীকরণ (i) এর (- 2, – 4), (0, -1) ও (4, 5) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এই সরলরেখা 3x – 2y = 2 সমীকরণের লেখ। আবার সমীকরণ (ii) এর (-2, – 5), (1, 0) ও (4, 5) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে আর একটি সরলরেখা পাওয়া গেল। এই সরলরেখা 5x – 3y = 5 সমীকরণের লেখ। প্রাপ্ত সরলরেখা দুটি A বিন্দুতে ছেদ করে। A বিন্দুর স্থানাঙ্ক উভয় সমীকরণকে সিদ্ধ করে।
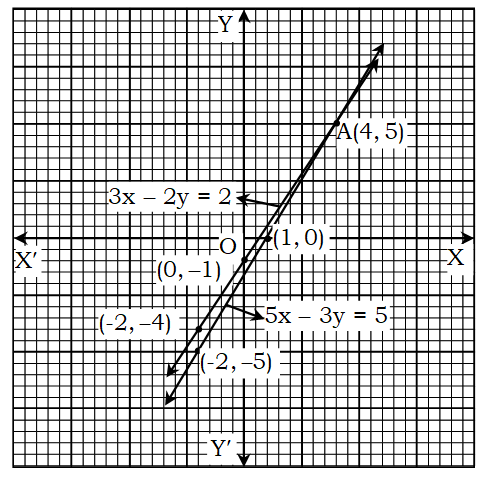
লেখ থেকে দেখা যায় A বিন্দুর ভুজ ও কোটি যথাক্রমে 4 ও 5.
∴ সমাধান (x, y) = (4, 5)
প্রশ্ন \ 5 \
2x + 3y = 13
সমাধান : প্রদত্ত সমীকরণদ্বয়,
…………….. (i)
2x + 3y = 13 …………..(ii)
সমীকরণ (i) থেকে পাই,
বা,
বা, 2y = 12 – 3x
বা, y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 2 | 4 |
| y | 6 | 3 | 0 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 6) (2, 3), (4, 0)|
আবার, সমীকরণ (2) থেকে পাই,
বা, 3y = 13 – 2x
বা, y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 1 | 2 | 5 |
| y | 5 | 3 | 1 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু ( -1, 5) (2, 3) (5, 1)
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের এক বাহুর দৈর্ঘ্যকে একক ধরি।
এখন সমীকরণ (1) এর (0, 6), (2, 3) ও (4, 0) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে একটি সরলখো পাওয়া গেল। এ টি সমীকরণের লেখ। আবার, সমীকরণ (2) এর (-1, 5), (2, 3) ও (5, 1) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে আরও একটি সরলরেখা পাওয়া গেল। এটি 2x + 3y = 13 সমীকরণের লেখ। সমীকরণ দুইটি পরস্পর A বিন্দুতে ছেদ করে।

লেখ থেকে দেখা যায় A বিন্দুর ভুজ 2 কোটি 3।
∴ সমাধান (x, y) = (2, 3)
প্রশ্ন \ 6 \ 3x + y = 6
5x + 3y = 12
সমাধান : প্রদত্ত সমীকরণদ্বয়
3x + y = 6 …………….. (i)
5x + 3y = 12 ………….(ii)
সমীকরণ (1) থেকে পাই,
y = 6 – 3x
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 1 | 4 |
| y | 6 | 3 | – 6 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 6), (1, 3), (4, – 6)।
আবার, সমীকরণ (2) থেকে পাই,
3y =12 – 5x
y=
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 3 | 6 |
| y | 4 | – 1 | – 6 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 4), (3, -1), (6, – 6)।
মনে করি, XOX’ ও YOY’ যথাক্রমে x অক্ষ ও y অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন ছক কাগজে সমীকরণ (1) এর (0, 6), (1, 3) ও (4, – 6) বিন্দুগুলো স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এটি 3x + y = 6 সমীকরণের লেখ। আবার, সমীকরণ (2) এর (0, 4), (3, -1) ও (6, – 6) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে আরও একটি সরলরেখা পাওয়া গেল। এটি 5x + 3y = 12 সমীকরণের লেখ। সরলরেখা দুইটি পরস্পর A বিন্দুতে ছেদ করে।

লেখ থেকে দেখা যায় A বিন্দুর ভুজ 32 বা, 1.5 ও কোটি 32 বা, 1.5
∴ সমাধান (x, y) = বা, (1·5, 1·5)
প্রশ্ন \ 7 \ 3x + 2y = 4
3x – 4y = 1
সমাধান : প্রদত্ত সমীকরণদ্বয়,
3x + 2y = 4 …………… (i)
3x – 4y = 1 …………… (ii)
সমীকরণ (i) থেকে পাই,
2y = 4 – 3x
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 0 | 2 |
| y | 5 | 2 | – 1 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (- 2, 5), (0, 2), (2, -1)।
আবার, সমীকরণ (ii) থেকে পাই,
– 4y = 1 – 3x
বা, 4y = 3x -1
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | -1 | 1 | 3 |
| y | -1 | 2 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (-1, -1), , (3, 2)।
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন, সমীকরণ (1) এর (-2, 5), (0, 2) ও (2, – 1) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে, একটি সরলরেখা পাওয়া গেল। এটি 3x + 2y = 4 সমীকরণের লেখ।
আবার, সমীকরণ (2) এর (-1, -1), ও (3, 2) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে আর একটি সরলরেখা পাওয়া গেল। এটি 3x – 4y = 1 সমীকরণের লেখ। সরলরেখা দুইটি পরস্পর A বিন্দুতে ছেদ করে।
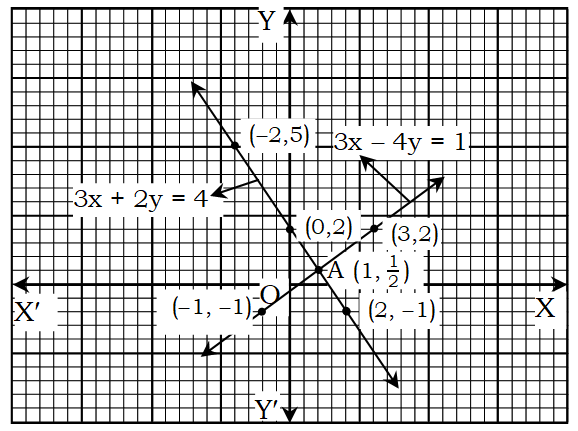
লেখ থেকে দেখা যায় A বিন্দুর ভুজ 1 ও কোটি 1/2।
∴ সমাধান (x, y) =
প্রশ্ন \ 8 \
সমাধান : প্রদত্ত সমীকরণদ্বয়,
…………….. (i)
…………….. (ii)
সমীকরণ (i) থেকে পাই,
বা,
বা, 2y = 18 – 3x
∴ y =
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 2 | 6 |
| y | 9 | 6 | 0 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 9) (2, 6), (6, 0)
আবার, সমীকরণ (ii) থেকে পাই,
∴ y = 18 – 6x
সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 2 | 3 | 4 |
| y | 6 | 0 | -6 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (2, 6) (3, 0), (4, – 6)।
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের এক বাহুর দৈর্ঘ্যকে একক ধরি। এখন সমীকরণ (1) এর (0, 9), (2, 6) ও (6, 0) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এটি সমীকরণের লেখ। আবার সমীকরণ (2) এর (2, 6), (3, 0) ও (4, – 6) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয়দিকে বর্ধিত করি। ফলে আরও একটি সরলরেখা পাওয়া গেল। এটি
সমীকরণের লেখ। সমীকরণ দুইটি পরস্পর A বিন্দুতে ছেদ করে।

লেখ থেকে দেখা যায় A বিন্দুর ভুজ 2 কোটি 6।
∴ সমাধান (x, y) = (2, 6)
প্রশ্ন \ 9 \ 3x + 2 = x – 2
সমাধান : প্রদত্ত সমীকরণ 3x + 2 = x – 2
ধরি, y = 3x + 2 …………. (i)
এবং y =y = x – 2 …………… (ii)
(1)নং সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 0 | 1 |
| y | – 4 | 2 | 5 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু ( – 2, – 4), (0, 2), (1, 5)।
আবার (2) নং সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | – 2 | 1 | 3 |
| y | – 4 | -1 | 1 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (- 2, – 4), (1, -1), (3, 1)।
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও ু- অক্ষ এবং o মূলবিন্দু। ছক কাগজের ক্ষুদ্রতম বর্গের দুই বাহুর দৈর্ঘ্যকে একক ধরি।
এখন, সমীকরণ (1) এর লেখের (-2, – 4), (0, 2) ও (1, 5) এর প্রতিরূপী বিন্দুগুলো লেখ কাগজে স্থাপন করি। এই বিন্দুগুলো যোগ করে একটি সরলরেখা পাওয়া গেল। সরলরেখাটিকে উভয় দিকে বর্ধিত করি। অতএব, এটিই y = 3x + 2 সমীকরণটির লেখ।
আবার, সমীকরণ (2) এর লেখের (- 2, – 4), (1, -1) ও (3, 1) এর প্রতিরূপী বিন্দুগুলো লেখ কাগজে স্থাপন করি। এই বিন্দুগুলো যোগ করে একটি সরলরেখা পাওয়া গেল। সরলরেখাটি উভয় দিকে বর্ধিত করি। অতএব, এটিই y = x – 2 সমীকরণটি লেখ।
ধরি, সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে অর্থাৎ, অ বিন্দু উভয় রেখার সাধারণ বিন্দু। অ এর স্থানাঙ্ক উভয় সমীকরণকে সিদ্ধ করে।
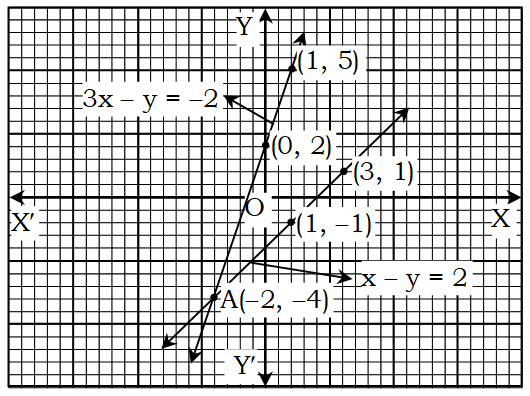
লেখ থেকে দেখা যায় যে, A বিন্দুর ভুজ = -2.
∴ সমাধান : x = -2
প্রশ্ন \ 10 \ 3x – 7 = 3 – 2x
সমাধান : প্রদত্ত সমীকরণ, 3x – 7 = 3 – 2x
ধরি, y = 3x – 7 ……………….. (i)
এবং y = 3 – 2x ………………… (ii)
সমীকরণ(i)-এ x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 3 | 5 |
| y | – 7 | 2 | 8 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, -7), (3, 2), (5, 8)
আবার, (2)নং সমীকরণটিতে x এর সুবিধামতো কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিচের ছকটি তৈরি করি :
| x | 0 | 2 | 4 |
| y | 3 | -1 | -5 |
∴ সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 3), (2, -1), (4, – 5)।
মনে করি, XOX’ ও YOY’ যথাক্রমে x-অক্ষ ও y অক্ষ এবং o মূলবিন্দু। উভয় অক্ষে ক্ষুদ্রতম বর্গের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি।
সমীকরণ (1) লেখের (0, -7), (3, 2) ও (5, 8) এর প্রতিরূপী বিন্দুগুলো লেখ কাগজে স্থাপন করি। এই বিন্দুগুলো যোগ করে একটি সরলরেখা পাওয়া গেল। সরলরেখাটিকে উত্তর দিকে বর্ধিত করি। অতএব, এটিই y = 3x – 7 সমীকরণটির লেখ।
সমীকরণ (2) লেখের (0, 3), (2, – 1) ও (4, -5) এর প্রতিরূপী বিন্দুগুলো লেখ কাগজে স্থাপন করি। এই বিন্দুগুলো যোগ করে একটি সরলরেখা পাওয়া গেল। সরলরেখাটিকে উভয় দিকে বর্ধিত করি। এটিই y = 3 – 2x সমীকরণটির লেখ।
ধরি, সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে অর্থাৎ অ বিন্দু উভয় রেখার সাধারণ বিন্দু। অ এর স্থানাঙ্ক উভয় সমীকরণকে সিদ্ধ করে।

লেখ থেকে দেখা যে, A বিন্দুর ভুজ = 2.
∴ সমাধান : x = 2
🔶🔶 এসএসসি সাধারণ গণিত সকল অধ্যায়
