এসএসসি গণিত অনুশীলনী ১২.৪ প্রশ্ন সমাধান

নবম দশম শ্রেণির বা এসএসসি গণিত ১২ অধ্যায়ের অনুশীলনী ১২.৪ প্রশ্ন সমাধান নিচে দেওয়া হলো। সেই সাথে এসএসসি গণিত বইয়ের সকল অধ্যায়ের সমাধান লিংক দেওয়া হলো।

নবম দশম শ্রেণির গণিত অনুশীলনী ১২.৪ প্রশ্ন সমাধান

বি.দ্রঃ ফন্ট দেখতে সমস্যা হলে Google Chrome ব্রাউজার ব্যবহার করুন।

প্রশ্ন \ 1 \ নিচের কোন শর্তে ax + by + c = 0 ও px + qy + r = 0 সমীকরণজোটটি সমঞ্জস ও পরস্পর অনির্ভরশীল হবে?
ক. $\frac{a}{p}{\rm{ }} \ne {\rm{ }}\frac{b}{q}$ (খ) $\frac{a}{p}{\rm{ = }}\frac{b}{q}{\rm{ = }}\frac{c}{r}$ (গ) $\frac{a}{p}{\rm{ = }}\frac{b}{q}{\rm{ }} \ne {\rm{ }}\frac{c}{r}$ (ঘ) $\frac{a}{p}{\rm{ = }}\frac{b}{q}$

প্রশ্ন \ 2 \ x + y = 4, x – y = 2 হলে, (x, y) এর মান নিচের কোনটি?
ক. (2, 4) খ. (4, 2) গ. (3, 1) ঘ. (1, 3)

প্রশ্ন \ 3 \x + y = 6 ও 2x = 4 হলে, y এর মান কত?
ক. 2 খ. 4 গ. 6 ঘ. 8

প্রশ্ন \ 4 \ নিচের কোনটির

x	0	2	4
y	-4	0	4

জন্য পাশের ছকটি সঠিক?

ক.y = x – 4 4 খ.y = 8 – x
গ.y = 4 – 2x ঘ.y = 2x – 4

প্রশ্ন \ 5 \ 2x – y = 8 এবংx – 2y = 4 হলে,x + y = কত?
ক. 0 খ. 4 গ. 8 ঘ. 12

প্রশ্ন \ 6 \x – y -4= 0 এবং 3x-3y-10 সমীকরণদ্বয়।
i. পরস্পর নির্ভরশীল।
ii. পরস্পর সমঞ্জস।
iii. এর কোনো সমাধান নেই।
উপরের তথ্যের ভিত্তিতে নিচের কোনটি সঠিক?
ক. ii খ. iii গ. i ও iii ঘ. ii ও iii

আয়তাকার একটি ঘরের মেঝের দৈর্ঘ্য, প্রস্থ অপেক্ষা 2 মিটার বেশি এবং মেঝের পরিসীমা 20 মিটার।
নিচের প্রশ্নগুলোর উত্তর দাও :
প্রশ্ন \ 7 \ ঘরটির মেঝের দৈর্ঘ্য কত মিটার?
ক. 10 খ. 8 গ. 6 ঘ. 4
ব্যাখ্যা : ধরি প্রস্থ = x মি. ∴ দৈর্ঘ্য : (x + 2) মি.
প্রশ্নমতে,
2(x + x + 2) = 20
বা, 2(2x + 2) = 20
বা, 4x + 4 = 20
বা, 4x = 20 – 4 = 16
∴ x = 4
∴ দৈর্ঘ্য = (4 + 2) মি. = 6 মি.

প্রশ্ন \ 8 \ ঘরটির মেঝের ক্ষেত্রফল কত বর্গমিটার?
ক. 24 খ. 32 গ. 48 ঘ. 80
ব্যাখ্যা : ক্ষেত্রফল = (6 × 4) বর্গ মি. = 24 বর্গ মি.

প্রশ্ন \ 9 \ ঘরটির মেঝে মোজাইক করতে প্রতি বর্গমিটারে 900 টাকা হিসেবে মোট কত খরচ হবে?
ক. 72000 খ. 43200 গ. 28800 ঘ. 21600
ব্যাখ্যা : প্রতি বর্গমিটার 900 টাকা হিসেবে মোজাইক করতে মোট খরচ
= (900 × 24) টাকা
= 21600 টাকা।

সহসমীকরণ গঠন করে সমাধান কর (10 -17) :
প্রশ্ন \ 10 \ কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সাথে 1 যোগ করলে ভগ্নাংশটি $\frac{{\bf{4}}}{{\bf{5}}}$ হবে। আবার, লব ও হরের প্রত্যেকটি থেকে 5 বিয়োগ করলে ভগ্নাংশটি $\frac{{\bf{1}}}{{\bf{2}}}$ হবে। ভগ্নাংশটি নির্ণয় কর।
সমাধান : মনে করি, ভগ্নাংশটির লব x এবং হর y
∴ ভগ্নাংশটি = $\frac{x}{y}$

1ম শর্তানুসারে, $\frac{{x + 1}}{{y + 1}}{\rm{ = }}\frac{4}{5}$ ………(i)
2য় শর্তানুসারে, $\frac{{x - 5}}{{y - 5}}{\rm{ = }}\frac{1}{2}$ ………..(ii)
সমীকরণ (i) হতে পাই,
5x + 5 = 4y + 4 [আড়গুণন করে]
বা, 5x – 4y = 4 – 5
∴ 5x – 4y = -1 ……………….(iii)
সমীকরণ (ii) হতে পাই,
2x – 10 = y – 5 [আড়গুণন করে]
বা, 2x-y = – 5 + 10
বা, 2x-y = 5
বা, 2x = y + 5
∴ x = $\frac{{y + 5}}{2}$ ………..(iv)
x এর মান সমীকরণ (iii) এ বসিয়ে পাই,
5 $\frac{{y + 5}}{2}$ 2 – 4y = – 1
বা, $\frac{{5y + 25 - 8y}}{2}$ = – 1
বা, 25 – 3y = – 2
বা, – 3y = – 2 – 25
বা, – 3y = – 27
∴ y= 9 [-3 দ্বারা ভাগ করে]
y এর মান সমীকরণ (iv) এ বসিয়ে পাই,
x = $\frac{{9 + 5}}{2}$

বা, x = 14/2
∴x = 7
নির্ণেয় ভগ্নাংশ $\frac{x}{y}$ = $\frac{7}{9}$

প্রশ্ন \ 11 \ কোনো ভগ্নাংশের লব থেকে 1 বিয়োগ ও হরের সাথে 2 যোগ করলে ভগ্নাংশটি $\frac{{\bf{1}}}{{\bf{2}}}$ হয়। আর লব থেকে 7 বিয়োগ এবং হর থেকে 2 বিয়োগ করলে ভগ্নাংশটি 1/3 হয়। ভগ্নাংশটি নির্ণয় কর।
সমাধান : মনে করি, ভগ্নাংশটির লব x এবং হর y
∴ ভগ্নাংশটি = $\frac{x}{y}$
1ম শর্তানুসারে, $\frac{{x - 1}}{{y + 2}}{\rm{ = }}\frac{1}{2}$ ………..(i)
2য় শর্তানুসারে, $\frac{{x - 7}}{{y - 2}}{\rm{ = }}\frac{1}{3}$ …………….(ii)
সমীকরণ (1) হতে পাই,
y + 2 = 2x – 2 [আড়গুণন করে]
বা, y= 2x – 2 – 2
∴ y= 2x – 4 … … (iii)
সমীকরণ (2) হতে পাই,
3x – 21 = y – 2 [আড়গুণন করে]
বা, 3x – 21 = 2x – 4 – 2 [∵ y= 2x – 4]
বা, 3x – 2x = 21 – 6
∴ x = 15
(iii) নং সমীকরণে x -এর মান বসিয়ে পাই,
∴ y= 2 × 15 – 4
= 30 – 4
= 26
নির্ণেয় ভগ্নাংশটি $\frac{x}{y}$ = $\frac{{15}}{{26}}$ .

প্রশ্ন \ 12 \ দুই অঙ্কবিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্ক দশক স্থানীয় অঙ্কের তিনগুণ অপেক্ষা 1 বেশি। কিন্তু অঙ্কদ্বয় স্থান বিনিময় করলে যে সংখ্যা পাওয়া যায়, তা অঙ্কদ্বয়ের সমষ্টির আটগুণের সমান। সংখ্যাটি কত?
সমাধান : মনে করি, একক স্থানীয় অঙ্ক x
এবং দশক স্থানীয় অঙ্ক y
∴ সংখ্যাটি = 10y + x
অঙ্কদ্বয় স্থান বিনিময় করলে প্রাপ্ত সংখ্যাটি 10x + y
1ম শর্তানুসারে, x = 3y + 1 …………………(1)
2য় শর্তানুসারে, 10x + y= 8(x + y)………..(2)
সমীকরণে (2) এ x = 3y + 1 বসিয়ে পাই,
10(3y + 1) + y= 8(3y + 1 + y)
বা, 30y + 10 + y= 24y + 8 + 8y
বা, 31y + 10 = 32 y + 8
বা, 31y – 32y= 8 – 10 [পক্ষান্তর করে]
বা, – y= -2
∴ y= 2 [-1 দ্বারা গুণ করে]
y এর মান সমীকরণ (1) এ বসিয়ে পাই, x = 3 × 2 + 1
= 6 + 1
= 7
∴ সংখ্যাটি = 10 × 2 + 7
= 20 + 7
= 27 (ans)

প্রশ্ন \ 13 \ দুই অঙ্কবিশিষ্ট একটি সংখ্যার অঙ্কদ্বয়ের অন্তর 4; সংখ্যাটির অঙ্কদ্বয় স্থান বিনিময় করলে যে সংখ্যা পাওয়া যায়, তার ও মূল সংখ্যাটির যোগফল 110; সংখ্যাটি নির্ণয় কর।
সমাধান : মনে করি, একক স্থানীয় অঙ্ক x
এবং দশক স্থানীয় অঙ্ক y
∴ সংখ্যাটি = 10y + x
অঙ্কদ্বয় স্থান বিনিময় করলে সংখ্যাটি = 10x + y
প্রথম শর্তানুসারে,
x– y= 4; যখন x >y … … … … … … (i)
y – x = 4; যখন x <y … … ….. … .. … (ii)
দ্বিতীয় শর্তানুসারে,
10y + x + 10x + y= 110 … … … … (iii)
সমীকরণ (i) ও (ii) থেকে পাই,
x = 4 + y … … … … … (iv) [যখন x >y]
y= 4 + x … … … … … (v) [যখন y > x]
সমীকরণ (iii) এ x -এর স্থলে 4 + y বসাই,
10y + 4 + y + 10 (4 + y) + y= 110
বা, 10y + 4 + y + 40 + 10y + y=110
বা, 22y= 110 – 40 – 4
বা, 22y= 66
বা, y= $\frac{{66}}{{22}}$

∴ y= 3
সমীকরণ (iv) এ y এর মান বসাই;
x = 4 + 3 = 7
∴ সংখ্যাটি = 10 × 3 + 7 = 30 + 7 = 37
আবার সমীকরণ (iii) এর y এর স্থলে 4 + x বসাই,
10(4 + x) + x + 10x + 4 + x = 110
বা, 40 +10x + x + 10x + 4 + x = 110
বা, 22x + 44 = 110
বা, 22x = 110 – 44
বা, 22x = 66
∴ x = 3 [উভয়পক্ষকে 22 দিয়ে ভাগ করে]
x এর মান সমীকরণ (v) এ বসাই,
y= 4 + 3 = 7
∴ সংখ্যাটি = 10 × 7 + 3 = 70 + 3 = 73
নির্ণেয় সংখ্যাটি 73 বা 37.

প্রশ্ন \ 14 \ মাতার বর্তমান বয়স তার দুই কন্যার বয়সের সমষ্টির চারগুণ। 5 বছর পর মাতার বয়স ঐ দুই কন্যার বয়সের সমষ্টির দ্বিগুণ হবে। মাতার বর্তমান বয়স কত?
সমাধান : মনে করি, দুই কন্যার বয়সের সমষ্টি x বছর
এবং মাতার বর্তমান বয়স 4 x বছর
5 বছর পর মাতার বয়স হবে = (4x + 5) বছর
এবং 5 বছর পর দুই কন্যার বয়স হবে = (x + 2 × 5) বছর
= (x + 10) বছর
প্রশ্নানুসারে, 4x + 5 = 2(x + 10)
বা, 4x + 5 = 2x + 20
বা, 4 x – 2x = 20 – 5
বা, 2x = 15
বা, x = $\frac{{15}}{2}$

∴ x = ${\rm{7 }}\frac{1}{2}$

∴ মাতার বর্তমান বয়স = $\left( {4 \times 7\frac{1}{2}} \right)$ বছর = $\left( {4 \times \frac{{15}}{2}} \right)$ বছর = 30 বছর
অতএব, মাতার বর্তমান বয়স 30 বছর। (ans)

প্রশ্ন \ 15 \ একটি আয়তক্ষেত্রের দৈর্ঘ্য 5 মিটার কম ও প্রস্থ 3 মিটার বেশি হলে ক্ষেত্রফল 9 বর্গমিটার কম হতো। আবার দৈর্ঘ্য 3 মিটার বেশি ও প্রস্থ 2 মিটার বেশি হলে ক্ষেত্রফল 67 বর্গমিটার বেশি হতো। ক্ষেত্রটির দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।
সমাধান : মনে করি, আয়তটির দৈর্ঘ্য x মিটার
এবং প্রস্থ y মিটার
∴ আয়তটির ক্ষেত্রফল = xy বর্গমিটার
1ম শর্তানুসারে, xy – (x – 5) (y + 3) = 9 … … … (i)
2য় শর্তানুসারে, (x + 3) (y + 2) – xy= 67 … … … (ii)
সমীকরণ (i) থেকে পাই,
xy – (x y – 5y + 3x – 15) = 9
বা, xy – xy + 5 y – 3x + 15 = 9
বা, 5 y – 3x = 9 – 15
বা, 5y – 3x = – 6
বা, 5y= 3x – 6 [পক্ষান্তর করে]
∴ y= 3x – 6 5 … … … … … (iii)
সমীকরণ (ii) থেকে পাই,
xy + 3y + 2x + 6 – xy= 67
বা, 3y + 2x = 67 – 6 = 61 … … … … (iv)
সমীকরণ (iv) এ y এর স্থলে $\frac{{3x - 6}}{5}$ বসাই,
3 × $\frac{{3x - 6}}{5}$ + 2x = 61
বা, 9x – 18 + 10x = 305 [উভয়পক্ষকে 5 দ্বারা গুণ করে]
বা, 19x = 305 + 18
বা, 19x = 323
বা, x = $\frac{{323}}{{19}}$

∴ x = 17
সমীকরণ (iii)-এ x এর মান বসাই,
y= $\frac{{3 \times 17 - 6}}{5}{\rm{ = }}\frac{{51 - 6}}{5}{\rm{ = }}\frac{{45}}{5}$

= 9
ক্ষেত্রটির দৈর্ঘ্য 17 মিটার এবং প্রস্থ 9 মিটার।

প্রশ্ন \ 16 \ একটি নৌকা দাঁড় বেয়ে স্রোতের অনুক‚লে ঘণ্টায় 15 কি.মি. যায় এবং স্রোতের প্রতিক‚লে যায় ঘণ্টায় 5 কি.মি.। নৌকার ও স্রোতের বেগ নির্ণয় কর।
সমাধান : মনে করি, দাঁড়ের বেগ ঘণ্টায় ী কি.মি.
এবং স্রোতের বেগ ঘণ্টায় ু কি.মি.
1ম শর্তানুসারে, x + y= 15 … … … … … (i)
2য় শর্তানুসারে, x- y= 5 … … … … … (ii)
[যেহেতু স্রোতের অনুক‚লে বেগ = দাঁড়ের বেগ + স্রোতের বেগ এবং স্রোতের প্রতিক‚লে বেগ = দাঁড়ের বেগ – স্রোতের বেগ]
সমীকরণ (i) থেকে পাই,
x = 15 -y … … … … … (iii)
সমীকরণ (ii) এ x এর স্থলে 15 -y বসাই,
15 – y – y= 5
বা, – 2y= 5 – 15
বা, – 2y= – 10
বা, y= $\frac{{ - 10}}{{ - 2}}$

∴ y= 5
সমীকরণ (iii)-এ y এর মান বসাই,
x = 15 – 5
= 10
নির্ণেয় স্রোতের বেগ ঘণ্টায় 5 কি.মি. এবং নৌকার বেগ 10 কি.মি./ঘণ্টা।

প্রশ্ন \ 17 \ একজন গার্মেন্টস শ্রমিক মাসিক বেতনে চাকরি করেন। প্রতিবছর শেষে একটি নির্দিষ্ট বেতনবৃদ্ধি পান। তার মাসিক বেতন 4 বছর পর 4500 টাকা ও 8 বছর পর 5000 টাকা হয়। তার চাকরি শুরুর বেতন ও বার্ষিক বেতন বৃদ্ধির পরিমাণ নির্ণয় কর।
সমাধান : মনে করি, চাকরি শুরুর বেতন x টাকা এবং বার্ষিক বেতন বৃদ্ধির পরিমাণ y টাকা।
4 বছরে বেতন বৃদ্ধি পায় = 4y টাকা
এবং 8 বছরে বেতন বৃদ্ধি পায় = 8y টাকা
1ম শর্তানুসারে x + 4y = 4500 ……………………..(i)
2য় শর্তানুসারে x + 8y= 5000 ……………………..(ii)
সমীকরণ (ii) থেকে (i) বিয়োগ করে পাই,
x + 8y – x – 4y = 5000 – 4500
বা, 4y = 500
বা, y= 500/4
∴ y= 125
y এর মান সমীকরণ (i) এ বসিয়ে পাই,
x + 4 × 125 = 4500
বা, x + 500 = 4500
বা, x = 4500 – 500
∴ x = 4000
সুতরাং চাকরি শুরুর বেতন 4000 টাকা এবং বার্ষিক বেতনবৃদ্ধি 125 টাকা।

প্রশ্ন \ 18 \ একটি সরল সমীকরণজোট x + y= 10
3x – 2y= 0
ক. দেখাও যে, সমীকরণজোটটি সমঞ্জস। এর কয়টি সমাধান আছে?
খ. সমীকরণজোটটি সমধান করে (x, y) নির্ণয় কর।
গ. সমীকরণদ্বয় দ্বারা নির্দেশিত সরলরেখাদ্বয় x-অক্ষের সাথে যে ত্রিভুজ গঠন করে তার ক্ষেত্রফল নির্ণয় কর।
সমাধান :
ক. প্রদত্ত সমীকরণজোট x + y= 10
3x – 2y= 0
x এর সহগদ্বয়ের অনুপাত 1/3
y এর সহগদ্বয়ের অনুপাত 1/-2
∴ $\frac{1}{3}{\rm{ }} \ne {\rm{ }}\frac{{ - 1}}{2}{\rm{ }}$ সমীকরণজোটটি সমঞ্জস। (দেখানো হলো)
ধ্রুবক পদদ্বয়ের অনুপাত 10/0
আবার, যেহেতু, $\frac{1}{3}{\rm{ }} \ne {\rm{ }}\frac{{ - 1}}{2}{\rm{ }} \ne {\rm{ }}\frac{{10}}{0}$
সুতরাং যোগ্যতার শর্তানুযায়ী সমীকরণজোটটি সমঞ্জস ও পরস্পর অনির্ভরশীল।
অতএব, এর একটিমাত্র সমাধান আছে।

খ. প্রদত্ত সমীকরণদ্বয়, x + y= 10 ……………….. (i)
3x – 2y= 0 ……………… (ii)
সমীকরণ (i) কে 2 দ্বারা গুণ করে (ii) এর সাথে যোগ করে পাই,
2x + 2y= 20
3x – 2y= 0
(+) করে, 5x = 20
বা, x = 20/5
∴ x = 4
x এর মান সমীকরণ (i) এ বসিয়ে পাই, 4 + y= 10
বা, y= 10 – 4
∴ y= 6
নির্ণেয় সমাধান : (x, y) = (4, 6)

গ. প্রদত্ত সমীকরণদ্বয় x + y= 10 ………………. (i)
3x – 2y= 0 ……………. (ii)
সমীকরণ (i) হতে পাই, y= 10 – x
এ সমীকরণের লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি :

x	-1	0	4	8
y	11	10	6	2

আবার, সমীকরণ (ii) হতে পাই, 2y= 3x
∴ y= $\frac{3}{2}{\rm{ x}}$

এ সমীকরণে লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি :

x	-2	0	2	4
y	-3	0	3	6

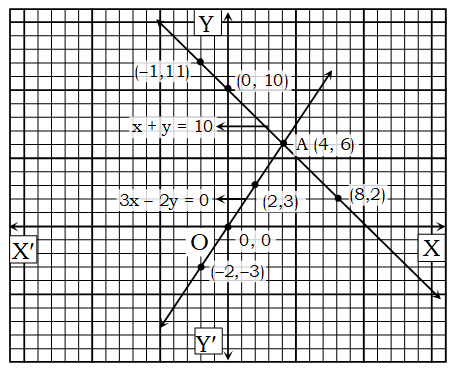
এসএসসি গণিত অনুশীলনী ১২.৪ প্রশ্ন সমাধান

মনে করি, X O X’ ও Y O Y’ যথাক্রমে x -অক্ষ ও y-অক্ষ
ছক কাগজের ক্ষুদ্রতম বর্গের প্রতিবাহুর দৈর্ঘ্যকে একক ধরে সমীকরণ (i) থেকে প্রাপ্ত লেখের (-1, 11) (0, 10), (4, 6), (8. 2) বিন্দুগুলো ছক কাগজে স্থাপন করি ও বিন্দুগুলো পরপর যোগ করে উভয় দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। আবার, সমীকরণ (ii) থেকে প্রাপ্ত লেখের (-2, -3), (0, 0), (2, 3), (4, 6) বিন্দুগুলো ছক কাগজে স্থাপন করে এগুলো পরস্পর সংযুক্ত করি এবং উভয়দিকে বর্ধিত করি। ফলে আর একটি সরলরেখা পাওয়া গেল। সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে। লেখ থেকে দেখা যায় সরলরেখাদ্বয় x অক্ষের সাথে ΔAOB গঠন করেছে। যার ভূমি 10 একক এবং উচ্চতা 6 একক।
∴ΔAOB এর ক্ষেত্রফল = $\left( {\frac{1}{2} \times 10 \times 6} \right)$ বর্গ একক
= 30 বর্গ একক। (ans)

প্রশ্ন \ 19 \ কোনো ভগ্নাংশের লবের সাথে 7 যোগ করলে ভগ্নাংশটির মান পূর্ণসংখ্যা 2 হয়। আবার হর হতে 2 বিয়োগ করলে ভগ্নাংশটির মান পূর্ণসংখ্যা 1 হয়।
ক. ভগ্নাংশটি $\frac{x}{y}$ ধরে সমীকরণজোট গঠন কর।
খ. সমীকরণজোটটি আড়গুণন পদ্ধতিতে সমাধান করে (x, y) নির্ণয় কর। ভগ্নাংশটি কত?
গ. সমীকরণজোটটির লেখ অঙ্কন করে (x, y) এর প্রাপ্ত মানের সত্যতা যাচাই কর।
সমাধান :
ক. মনে করি, ভগ্নাংশটির লব x এবং হর y
∴ ভগ্নাংশটি = $\frac{x}{y}$

1ম শর্তানুসারে, $\frac{{x + 7}}{y}$ = 2 ………………… (i)
2য় শর্তানুসারে, $\frac{x}{{y - 2}}$ = 1 ………………… (ii)
নির্ণেয় সমীকরণজোট, $\frac{{x + 7}}{y}$ = 2
$\frac{x}{{y - 2}}$ = 1

খ. সমীকরণ (i) হতে পাই,
x + 7 = 2y [আড়গুণন করে]
বা, x – 2y + 7 = 0 …………………. (iii)
সমীকরণ (2) হতে পাই,
x = y – 2
বা, x – y + 2 = 0 ………………..(iv)
সমীকরণ (ii) ও (iv) হতে আড়গুণন পদ্ধতিতে পাই,

$\frac{x}{{( - 2) \times 2 - ( - 1) \times 7}} = \frac{y}{{1 \times 7 - 1 \times 2}} = \frac{1}{{1 \times ( - 1) - 1 \times ( - 2)}}$

বা, $\frac{x}{{ - 4 + 7}}{\rm{ = }}\frac{y}{{7 - 2}}{\rm{ = }}\frac{1}{{ - 1 + 2}}$

বা, $\frac{x}{3}{\rm{ = }}\frac{y}{5}{\rm{ = }}\frac{1}{1}$

∴ $\frac{x}{3}$ = 1 আবার, $\frac{y}{5}$ = 11
বা, x = 3 বা, y= 5
∴ x = 3 ∴ y= 5
নির্ণেয় সমাধান : (x, y) = (3, 5)
এবং ভগ্নাংশটি = $\frac{3}{5}$

গ. সমীকরণ (iii) হতে পাই, -2y= – x – 7
বা, 2y= x + 7 [-1 দ্বারা গুণ করে]
∴ y= $\frac{{x + 7}}{y}$
এ সমীকরণের লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি :

x	– 3	1	3	7
y	2	4	5	7

আবার, সমীকরণ (iv) হতে পাই, – y= – x – 2
বা, y= x + 2
এ সমীকরণে লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি :

x	– 2	0	4	7
y	0	2	6	9

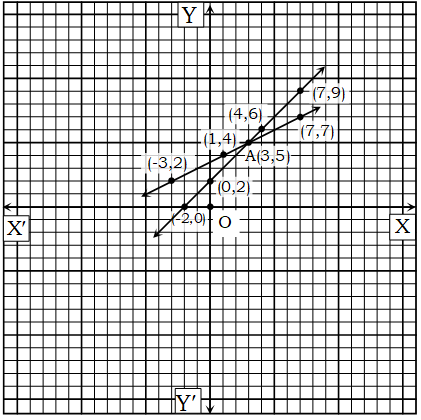
নবম দশম শ্রেণির গণিত অনুশীলনী ১২.৪ প্রশ্ন সমাধান

মনে করি, XOX’ ও YOY’ যথাক্রমে x -অক্ষ ও y-অক্ষ এবং ঙ মূলবিন্দু।
ছক কাগজের ক্ষুদ্রতম বর্গের প্রতিবাহুর দৈর্ঘ্যকে একক ধরে সমীকরণ (3) থেকে পাই (-3, 2), (1, 4), (3, 5) ও (7, 7) বিন্দুগুলো ছক কাগজে স্থাপন করি ও বিন্দুগুলো পরপর যোগ করে উভয়দিকে বর্ধিত করি। ফলে একটি সরলরেখা পাওয়া গেল। এটিই সমীকরণ (3) এর লেখ। আবার, সমীকরণ (4) থেকে প্রাপ্ত লেখের (-2, 0), (0, 2), (4, 6) ও (7, 9) বিন্দুগুলো ছক কাগজে স্থাপন করে যোগ করি এবং উভয় দিকে বর্ধিত করি। ফলে আর একটি সরলরেখা পাওয়া গেল। এটি সমীকরণ (4) এর লেখ।
(3) ও (4) সরলরেখাদ্বয় পরস্পর A বিন্দুতে ছেদ করে। লেখ থেকে দেখা যায় অ বিন্দুর স্থানাঙ্ক (3, 5) (খ) নং এর প্রাপ্ত মানের সাথে (গ) নং এর মানের সত্যতা যাচাই করা হলো।

20. দুইটি বহুভূজের বাহু সংখ্যা 17 এবং এদের কর্ণের সংখ্যা 53 হলে প্রত্যেক বহুভুজের বাহুর সংখ্যা কত?

সমাধানঃ

আমরা জানি,

বহুভুজের বাহুর সংখ্যা n হলে,

কর্ণের সংখ্যা= $\frac{{n(n - 3)}}{2}$

ধরি, 1ম বহুভূজের বাহুর সংখ্যা x

এবং 2 বহুভূজের বাহুর সংখ্যা y (x>y)

1ম বহুভূজের কর্ণের সংখ্যা= $\frac{{n(n - 3)}}{2}$

2য় বহুভূজের কর্ণের সংখ্যা= $\frac{{y(y - 3)}}{2}$

শর্তমতে,

x+y=17…………….(i)

$\frac{{n(n - 3)}}{2}$ + $\frac{{y(y - 3)}}{2}$ = 53

বা, x(x-3)+y(y-3)=53✕2

বা, x²-3x+y²-3y=106

বা, x²+y²-3(x+y)=106

বা, x²+y²-3.17=106

বা, x²+y²-51=106

বা, x²+y²=106+51

বা, x²+y²=157………….(iii)

বা, (x+y)²-2xy=157

বা, (17)²-2xy=157

বা, 289-2xy=157

বা, 289-157=2xy

বা, 2xy=132

বা, xy=66

আবার,

x²+y²=157

বা, (x-y)²+2xy=157

বা, (x-y)²+2.66=157

বা, (x-y)²+132=157

বা, (x-y)²=157-132

বা, (x-y)²=25

বা, x-y=5…………..(iv)

(i)+(iv) করে পাই,

2x=22

বা, x=22/2

বা, x=11

x এর মান (i) নং এ বসিয়ে পাই,

11+y=17

বা, y=17-11

বা, y=6

∴ 1ম বহুভূজের বাহুর সংখ্যা 11 টি

2য় বহুভূজের বাহুর সংখ্যা 6 টি

21. শিক্ষক বললেন একটি কাজ একা বা ছাত্র-ছাত্রীর জুটি করতে পারবে। ছাত্রদের 2/3 এবং ছাত্রীদের 3/5 অংশ জুটি বেধে কাজটি করলো। শ্রেণির কত ভাগ ছাত্র-ছাত্রী একা কাজটি করলো?

সমাধানঃ

ধরি, ছাত্র সংখ্যা x ও ছাত্রী সংখ্যা y

জুটি করে কাজ করা

ছাত্র সংখ্যা= $\frac{{2x}}{3}$

জুটি করে কাজ করা

ছাত্রী সংখ্যা= $\frac{{3y}}{5}$

একা কাজ করা ছাত্র সংখ্যা = $x - \frac{{2x}}{3} = \frac{x}{3}$

একা কাজ করা ছাত্রী সংখ্যা = $y - \frac{{3y}}{5} = \frac{{2y}}{5}$

শর্ত অনুসারে পাই, $\frac{{2x}}{3} = \frac{{3y}}{5}$

$x = \frac{{9y}}{{10}}$ . . . . . .(i)

মোট একা করল = $\frac{x}{3} + \frac{{2y}}{5}$

$= \frac{{\frac{{9y}}{{10}}}}{3} + \frac{{2y}}{5}$ [(i) হতে]

$= \frac{{3y}}{{10}} + \frac{{2y}}{5} = \frac{{3y + 4y}}{{10}}$

$= \frac{{7y}}{{10}}$

মোট শিক্ষার্থী = x+ y

$= \frac{{9y}}{{10}} + y = \frac{{9y + 10y}}{{10}}$

$= \frac{{19y}}{{10}}$

∴ নির্ণেয় অনুপাত = $= \frac{{\frac{{7y}}{{10}}}}{{\frac{{19y}}{{10}}}} = \frac{7}{{10}}$

22. 100 ও 200 মিটার দীর্ঘ দুইটি ট্রেন সমবেগে সামনা সামনি অতিক্রম করতে 5 সেকেন্ড সময় লাগে কিন্তু একি দিকে চললে অতিক্রম করতে 15 সেকেন্ড সময় লাগে। ট্রেন দুইটির বেগ নির্ণয় কর
সমাধানঃ

ধরি, 100 মিটার দৈর্ঘ্যের ট্রেনের বেগ V_x কিমি/সেকেন্ড এবং 200 মিটার দৈর্ঘ্যের ট্রেনের বেগ V_y কিমি/সেকেন্ড
প্রশ্নমতে,
5(V_x+V_y)=300
বা, V_x+V_y= $\frac{{300}}{5}$

বা, V_x+V_y=60………(i)
এবং,
15(V_x-V_y)=300
বা, V_x-V_y= $\frac{{300}}{{15}}$

বা, V_x-V_y=20……..(ii)
(i)+(ii) করে পাই,
2V_x=80
বা, V_x= $\frac{{80}}{2}$

বা, V_x=40
(i)-(ii) করে পাই,
2V_y=40
বা, V_y= $\frac{{40}}{2}$

বা, V_y=20
∴100 মিটার দৈর্ঘ্যের ট্রেনের বেগ 40 কিমি/সেকেন্ড এবং 200 মিটার দৈর্ঘ্যের ট্রেনের বেগ 20 কিমি/সেকেন্ড

23. কমপক্ষে কতগুলো ক্রমিক পূর্ণসংখ্যা নিলে তাঁর গুণফল অবশ্যই 5040 দ্বারা বিভজ্য হবে?

সমাধানঃ

2|5040
2|2520
2|1260
2|630
3|315
3|105
5|35
7
∴ 5040

=2✕2✕2✕2✕3✕3✕5✕7
=1✕2✕2✕2✕2✕3✕3✕5✕7
=1✕2✕3✕(2✕2)✕5✕(2✕3)✕7
=1✕2✕3✕4✕5✕6✕7
1 থেকে 7 পর্যন্ত ক্রমিক সংখ্যা 7টি।
∴ কমপক্ষে 7টি ক্রমিক পূর্ণসংখ্যা নিলে তাঁর গুণফল অবশ্যই 5040 দ্বারা বিভজ্য হবে।

24. ঘড়ির ঘন্টা এবং মিনিটের কাঁটা পরস্পরের সঙ্গে 30 ডিগ্রি কোণ করে কত বার ঘোরে? সময়গুলো নির্ণয় কর।

সমাধানঃ

12 ঘন্টার মধ্যে ঘন্টা ও মিনিটের কাঁটা 30° কোণ উৎপন্ন করে 22 বার।
তাহলে, 24 ঘন্টার মধ্যে ঘন্টা ও মিনিটের কাঁটা 30° কোণ উৎপন্ন করে 44 বার।
সময়গুলো নিন্মরুপঃ

12 :5 $\frac{5}{{11}}$