নবম দশম শ্রেণি বা এসএসসি গণিত ৮ অধ্যায় বৃত্ত অনুশীলনীর ৮.১ প্রশ্ন সমাধান নিচে দেওয়া হলো। নবম-দশম শ্রেণির গণিত অন্যান্য অধ্যায়গুলো সমাধান দেখতে পোস্টের নিচে দেওয়া লিংকে প্রবেশ করুন।

এসএসসি গণিত অনুশীলনী ৮.১ প্রশ্ন সমাধান

প্রশ্ন \ 1 \ প্রমাণ কর যে, কোনো বৃত্তের দুইটি জ্যা পরস্পরকে সমদ্বিখণ্ডিত করলে তাদের ছেদবিন্দু বৃত্তটির কেন্দ্র হবে।
সমাধান : সাধারণ নির্বচন : প্রমাণ করতে হবে যে, কোনো বৃত্তের দুইটি জ্যা পরস্পরকে সমদ্বিখণ্ডিত করলে তাদের ছেদবিন্দু বৃত্তটির কেন্দ্র হবে।

বিশেষ নির্বচন : মনে করি, ABCD বৃত্তের AB ও CD দুইটি জ্যা পরস্পরকে E বিন্দুতে সমদ্বিখণ্ডিত করেছে।
প্রমাণ করতে হবে যে, E-ই বৃত্তের কেন্দ্র।
অঙ্কন : বৃত্তটির কেন্দ্র E না ধরে O ধরি এবং O, E যোগ করি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) O বৃত্তের কেন্দ্র এবং AB জ্যা এর মধ্যবিন্দু E
[জানা আছে যে, বৃত্তের ব্যাস ভিন্ন কোনো জ্যা এর মধ্যবিন্দু এবং কেন্দ্রের সংযোজক রেখাংশ ঐ জ্যা এর ওপর লম্ব]
∴ OE ⊥ AB অর্থাৎ ∠OEA = এক সমকোণ
(2) আবার, O বৃত্তের কেন্দ্র এবং CD জ্যা এর মধ্যবিন্দু E
∴ OE ⊥ CD অর্থাৎ ∠OEC = এক সমকোণ
(3) যেহেতু AB এবং CD দুইটি পরস্পরচ্ছেদী সরলরেখা।
∴ ∠OEA এবং ∠OEC উভয়ই এক সমকোণ হতে পারে না।
(৪) সুতরাং E ব্যতীত অন্য কোনো বিন্দু বৃত্তের কেন্দ্র হতে পারে না।
∴ E বিন্দুটি ABCD বৃত্তের কেন্দ্র। [প্রমাণিত]

প্রশ্ন \ 2 \ প্রমাণ কর যে, দুইটি সমান্তরাল জ্যা-এর মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যাদ্বয়ের ওপর লম্ব।
সমাধান : সাধারণ নির্বচন : প্রমাণ করতে হবে যে, দুইটি সমান্তরাল জ্যায়ের মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যাদ্বয়ের ওপর লম্ব।

বিশেষ নির্বচন : মনে করি, ABCD বৃত্তের কেন্দ্র O। AB এর মধ্যবিন্দু E এবং CD এর মধ্যবিন্দু F এবং AB॥CD। প্রমাণ করতে হবে যে, EF কেন্দ্রগামী এবং AB ও CD এর ওপর লম্ব।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) F, CD এর মধ্যবিন্দু এবং OF কেন্দ্র ও জ্যা-এর মধ্যবিন্দুর সংযোজক রেখাংশ।
∴ OF, CD এর ওপর লম্ব। [বৃত্তের কেন্দ্র ও জ্যায়ের মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যায়ের ওপর লম্ব]
এবং ∠OFC = এক সমকোণ।
(2) আবার, E, AB এর মধ্যবিন্দু হওয়ায় OE , AB এর ওপর লম্ব এবং ∠AEO = এক সমকোণ। [একই কারণে]
∴ ∠AEO = ∠OFC [একান্তর কোণ]
(3) AB ॥ CD হওয়ায় EF ছেদক।
অর্থাৎ E, O, F একই সরলরেখা।
অতএব, EF কেন্দ্রগামী এবং EF⊥CD এবং FE⊥AB. [প্রমাণিত]

প্রশ্ন \ 3 \ কোনো বৃত্তের AB ও AC জ্যা দুইটি অ বিন্দুগামী ব্যাসার্ধের সাথে সমান কোণ উৎপন্ন করে। প্রমাণ কর যে, AB = AC.
সমাধান :

বিশেষ নির্বচন : মনে করি, ABC বৃত্তের কেন্দ্র O। AB ও AC জ্যা দুইটি OA ব্যাসার্ধের সাথে সমান কোণ উৎপন্ন করে অর্থাৎ ∠BAO = ∠CAO।
প্রমাণ করতে হবে যে, AB = AC.
অঙ্কন : O হতে AB এর ওপর OM এবং AC এর ওপর ON লম্ব আঁকি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) OM,AB এর ওপর লম্ব হওয়ায়, OM, AB কে সমদ্বিখণ্ডিত করে।
অর্থাৎ, AM = 1/2 AB
(2) আবার, ON, AC এর ওপর লম্ব হওয়ায়, AN = 1/2 AC
(3) এখন, ΔAOM ও ΔAON এর মধ্যে
∠AMO = ∠ANO [সমকোণ বলে]
∠MAO = ∠NAO [কল্পনা]
এবং AO সাধারণ বাহু।
∴ ত্রিভুজ দুটি সর্বসম।
অতএব, AM = AN
অর্থাৎ 1/2 AB = 1/2 AC
∴ AB = AC [প্রমাণিত]

প্রশ্ন \ ৪ \ চিত্রে O বৃত্তের কেন্দ্র এবং জ্যা AB = জ্যা AC। প্রমাণ কর যে, ∠BAO = ∠CAO.

সমাধান :

বিশেষ নির্বচন : মনে করি, ABC বৃত্তের O কেন্দ্র এবং জ্যা AB = জ্যা AC। AO কেন্দ্রগামী ব্যাসার্ধ।
প্রমাণ করতে হবে যে, ∠BAO = ∠CAO.
অঙ্কন : O, B এবং O, C যোগ করি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) ΔAOB ও ΔAOC এর মধ্যে
AB = AC [দেওয়া আছে]
BO = CO [একই বৃত্তের ব্যাসার্ধ]
এবং AO বাহু সাধারণ। [বাহু-বাহু-বাহু উপপাদ্য]
∴ ত্রিভুজদ্বয় সর্বসম।
অতএব, ∠BAO = ∠CAO। [প্রমাণিত]

প্রশ্ন \ ৫ \ কোনো বৃত্ত একটি সমকোণী ত্রিভুজের শীর্ষবিন্দুগুলো দিয়ে যায়। দেখাও যে, বৃত্তটির কেন্দ্র অতিভুজের মধ্যবিন্দু।
সমাধান : সাধারণ নির্বচন : কোনো বৃত্ত একটি সমকোণী ত্রিভুজের শীর্ষবিন্দুগুলো দিয়ে যায়। দেখাতে হবে যে, বৃত্তটির কেন্দ্র অতিভুজের মধ্যবিন্দু।

বিশেষ নির্বচন : মনে করি, সমকোণী ΔABC এর ∠B = এক সমকোণ এবং AC অতিভুজ।
A, B, C শীর্ষবিন্দু দিয়ে একটি বৃত্ত আঁকা হলো। মনে করি, বৃত্তটির কেন্দ্র O। দেখাতে হবে যে, কেন্দ্র O অতিভুজ AC এর মধ্যবিন্দু।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) ΔABC-এর
∠ABC = এক সমকোণ [কল্পনা]
∴ ∠ABC, O কেন্দ্রবিশিষ্ট বৃত্তের অর্ধবৃত্তস্থ কোণ।
[∵ অর্ধবৃত্তস্থ কোণ এক সমকোণ]
(2) A, B, C বিন্দুগামী বৃত্তের ব্যাস AC।
সুতরাং বৃত্তের কেন্দ্র O, ব্যাস AC এর উপর অবস্থিত।
∴ OA = OC [একই বৃত্তের ব্যাসার্ধ বলে]
∴ বৃত্তের কেন্দ্র O, A তিভুজ AC এর মধ্যবিন্দু। [দেখানো হলো]

প্রশ্ন \ ৬ \ দুইটি সমকেন্দ্রিক বৃত্তের একটির AB জ্যা অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। প্রমাণ কর যে, AC = BD.
সমাধান :

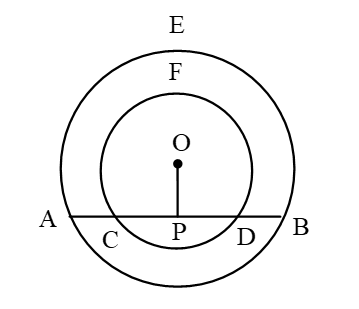
বিশেষ নির্বচন : মনে করি, ABE ও CDF বৃত্ত দুইটির কেন্দ্র O। ABE বৃত্তের জ্যা AB, CDF বৃত্তকে C ও D বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, AC = BD।
অঙ্কন : O হতে AB বা CD এর ওপর OP লম্ব আঁকি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) OP, CD এর ওপর লম্ব হওয়ায় OP, CD-কে সমদ্বিখণ্ডিত করে।
অর্থাৎ CP = PD [বৃত্তের কেন্দ্র হতে কোনো জ্যা এর
ওপর অঙ্কিত লম্ব ঐ জ্যাকে সমদ্বিখণ্ডিত করে]
(2) আবার, OP, AB এর ওপর লম্ব হওয়ায়, OP, AB-কে সমদ্বিখণ্ডিত করে।
অর্থাৎ, AP = BP [একই]
এখন, AP = AC + CP
এবং BP = PD + BD
সুতরাং AC + CP = PD + BD [∵ AP = BP]
∴ AC = BD [প্রমাণিত] [∵ CP = PD]

প্রশ্ন \ ৭ \ বৃত্তের দুইটি সমান জ্যা পরস্পরকে ছেদ করলে দেখাও যে, তাদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।
সমাধান : সাধারণ নির্বচন : বৃত্তের দুইটি সমান জ্যা পরস্পরকে ছেদ করলে, দেখাতে হবে যে, তাদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।

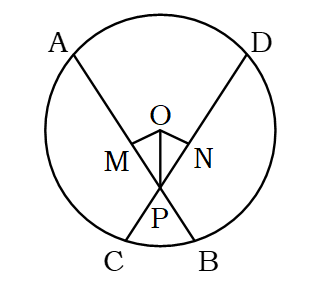
বিশেষ নির্বচন : মনে করি, ABCD বৃত্তের কেন্দ্র O। AB ও CD দুটি সমান জ্যা পরস্পরকে P বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, AP = PD এবং PB = PC.
অঙ্কন : O হতে AB এর ওপর OM এবং CD এর ওপর ON লম্ব আঁকি। O, চ যোগ করি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) MOP ও NOP সমকোণী ত্রিভুজ দুইটির মধ্যে
OM = ON [সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী]
এবং OP সাধারণ অতিভুজ।
∴ ত্রিভুজ দুইটি সর্বসম।
∴ PM = PN ………………………………….. (i)
(2) এখন, OM, AB এর ওপর লম্ব হওয়ায়,
AM = 1/2 AB [বৃত্তের কেন্দ্র হতে কোনো জ্যায়ের ওপর অঙ্কিত লম্ব ঐ জ্যাকে সমদ্বিখণ্ডিত করে]
(3) ON, CD এর ওপর লম্ব হওয়ায়,
DN = 1/2 CD [একই]
যেহেতু, AB = CD
∴ AM = DN ……………………………. (ii)
(৪) সমীকরণ (i) ও (ii) যোগ করে পাই,
PM + AM = PN + DN
বা, AP = PD
(৫) আবার, AB = CD
বা, AB – AP = CD – PD
বা, PB = PC
অতএব, AP = PD এবং PB = PC. [দেখানো হলো]

প্রশ্ন \ ৮ \ প্রমাণ কর যে, বৃত্তের সমান জ্যা এর মধ্যবিন্দুগুলো সমবৃত্ত।
সমাধান : সাধারণ নির্বচন : প্রমাণ করতে হবে যে, বৃত্তের সমান জ্যা এর মধ্যবিন্দুগুলো সমবৃত্ত।

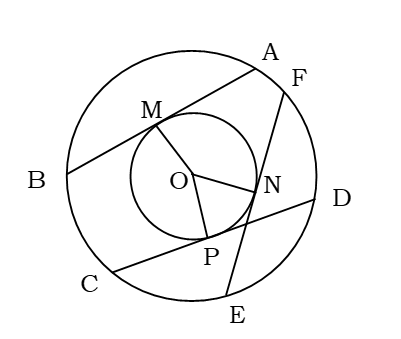
বিশেষ নির্বচন : মনে করি, ABCEDF বৃত্তে O কেন্দ্র। AB, CD এবং EF তিনটি পরস্পর সমান সমান জ্যা। M, N এবং P সমান জ্যা’গুলোর মধ্যবিন্দু।
প্রমাণ করতে হবে যে, M, N এবং P সমবৃত্ত।
অঙ্কন : O ও M, O ও N এবং O ও P যোগ করি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) যেহেতু M, AB এর মধ্যবিন্দু এবং OM কেন্দ্রগামী রেখাংশ।
∴ OM, AB এর উপর লম্ব। [বৃত্তের কেন্দ্র ও ব্যাস ভিন্ন কোনো জ্যা এর মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যা এর ওপর লম্ব]
(2) OP, CD এর ওপর লম্ব। [একই কারণ]
(3) ON, EF এর উপর লম্ব। [একই কারণ]
(৪) OM = OP = ON [বৃত্তের সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী]
সুতরাং O কে কেন্দ্র করে OM অথবা ON অথবা OP এর সমান ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে M, N ও P বিন্দু দিয়ে যাবে।
অতএব, M, N ও P সমবৃত্ত। [প্রমাণিত]

প্রশ্ন \ ৯ \ দেখাও যে, ব্যাসের দুই প্রান্ত থেকে তার বিপরীত দিকে দুইটি সমান জ্যা অঙ্কন করলে তারা সমান্তরাল হয়।
সমাধান : সাধারণ নির্বচন : দেখাতে হবে যে, ব্যাসের দুই প্রান্ত থেকে তার বিপরীত দিকে দুইটি সমান জ্যা অঙ্কন করলে তারা সমান্তরাল হয়।

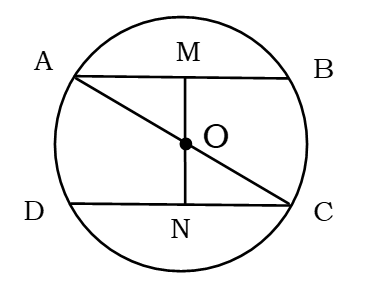
বিশেষ নির্বচন : মনে করি, ABCD বৃত্তের O কেন্দ্র এবং AC ব্যাস। AB ও CD দুইটি সমান সমান জ্যা AC ব্যাসের বিপরীত দিকে অবস্থিত।
প্রমাণ করতে হবে যে, AB ॥CD
অঙ্কন : O হতে AB এর ওপর OM এবং CD এর ওপর ON লম্ব আঁকি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) OM, AB এর ওপর লম্ব হওয়ায়,
AM = 1/2 AB [কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা-এর ওপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে]
(2) ON, CD এর ওপর লম্ব হওয়ায়, CN = 1/2 CD [একই]
(3) যেহেতু, AB = CD
∴ AM = CN
(৪) ΔAOM ও ΔCON
এর মধ্যে AM = CN
AO = OC [একই বৃত্তের ব্যাসার্ধ বলে]
এবং OM=ON [সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী বলে]
∴ ত্রিভুজদ্বয় সর্বসম।
∴ ∠A = ∠C
কিন্তু কোণ দুইটি AC রেখার বিপরীত পাশে অবস্থিত।
সুতরাং কোণ দুইটি একান্তর হওয়ায় AB ॥CD. [দেখানো হলো]

প্রশ্ন \ 1০ \ দেখাও যে, ব্যাসের দুই প্রান্ত থেকে তার বিপরীত দিকে দুইটি সমান্তরাল জ্যা আঁকলে তারা সমান হয়।
সমাধান : সাধারণ নির্বচন : দেখাতে হবে যে, ব্যাসের দুই প্রান্ত থেকে তার বিপরীত দিকে দুইটি সমান্তরাল জ্যা আঁকলে তারা সমান হয়।

বিশেষ নির্বচন : মনে করি, ABCD বৃত্তের O কেন্দ্র এবং AC ব্যাস। AC ব্যাসের বিপরীত পাশে AB॥CD দুইটি জ্যা। প্রমাণ করতে হবে যে, AB = CD.
অঙ্কন : O হতে AB এর ওপর OM এবং CD এর ওপর ON লম্ব আঁকি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) OM, AB জ্যা এর ওপর লম্ব হওয়ায়,
AM = 1/2 AB [কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা-এর ওপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে]
(2) ON, CD জ্যা এর ওপর লম্ব হওয়ায়,
CN = 1/2 CD. [ একই ]
(3) ΔAOM ও ΔCON এর মধ্যে
∠AMO = ∠CNO [সমকোণ বলে]
∠MAO = ∠NCO [একান্তর কোণ বলে]
এবং AO = CO [একই বৃত্তের ব্যাসার্ধ বলে]
∴ ত্রিভুজদ্বয় সর্বসম।
∴ AM = CN
(৪) অর্থাৎ 1/2 AB = 1/2 CD
অতএব, AB = CD [দেখানো হলো]

প্রশ্ন \ 11 \ দেখাও যে, বৃত্তের দুইটি জ্যা এর মধ্যে বৃহত্তর জ্যা-টি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর।
সমাধান : সাধারণ নির্বচন : দেখাতে হবে যে, বৃত্তের দুইটি জ্যা-এর মধ্যে বৃহত্তর জ্যাটি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর।

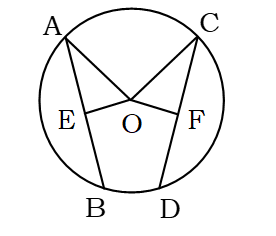
বিশেষ নির্বচন : মনে করি, ABDC বৃত্তের O কেন্দ্র। AB ও CD দুইটি জ্যা-এর মধ্যে AB > CD। OE এবং OF কেন্দ্র O থেকে যথাক্রমে AB ও CD এর ওপর লম্ব। দেখাতে হবে যে, OE < OF.
অঙ্কন : O, A এবং O, C যোগ করি।
প্রমাণ :
ধাপসমূহ যথার্থতা
(1) OE , AB এর ওপর লম্ব হওয়ায়,
AE = 1/2 AB [কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা-এর ওপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে]
(2) এবং OF, CD এর ওপর লম্ব হওয়ায়,
CF = 1/2 CD [একই]
(3) AOE সমকোণী ত্রিভুজে AO অতিভুজ
∴ OA² = OE ² + AE² …………………(i)
[পিথাগোরাসের উপপাদ্য]
(৪) আবার, COF সমকোণী ত্রিভুজে CO অতিভুজ
∴ OC2 = OF² + CF² ……………………..(ii)
(৫) AO এবং OC একই বৃত্তের ব্যাসার্ধ হওয়ায়, OA = OC [একই]
সুতরাং, OE ² + AE² = OF² + CF² ……………….(iii)
(৬) কিন্তু AB > CD হওয়ায়, 1/2 AB > 1/2 CD
বা, AE > CF
∴ AE² > CF²
সমীকরণ (iii) নং থেকে দেখা যায়,
AE² যদি CF² থেকে বৃহত্তর হয় তবে OE ², OF² থেকে ক্ষুদ্রতর হবে।
সুতরাং OE ² < OF²
∴ OE < OF. [দেখানো হলো]

---

🔶🔶 এসএসসি গণিত অনুশীলনী 11.1

🔶🔶 এসএসসি সাধারণ গণিত সকল অধ্যায়