৬ষ্ঠ শ্রেণির গণিত ৭ অধ্যায় ব্যাবহারিক জ্যামিতি সমাধান নিচে দেওয়া হলো। সেই সাথে ষষ্ঠ শ্রেণির গণিত বইয়ের  সকল অধ্যায় ও অনুশীলনীর সমাধান লিংক নিচে দেওয়া আছে সেখান থেকে আপনারা সব উত্তর পেয়ে যাবেন।

৬ষ্ঠ শ্রেণির গণিত অনুশীলনী ৭ ব্যাবহারিক জ্যামিতি

প্রশ্ন \ ১ \ ২৮° কোণের সম্পূরক কোণ কত?
(ক) ৬২° (খ) ১১৮° ✅১৫২° (ঘ) ৩৩২°
ব্যাখ্যা : আমরা জানি, দুইটি সন্নিহিত কোণের পরিমাপের যোগফল ১৮০° হলে কোণ দুইটির একটি অপরটির সম্পূরক কোণ।
∴ ২৮° কোণের সম্পূরক কোণ = ১৮০° – ২৮° = ১৫২°

প্রশ্ন \ ২ \ ৩৭° কোণের বিপ্রতীপ কোণ কত?
(ক) ৫৩° ✅ ৩৭° (গ) ১২৭° (ঘ) ১৪৩°

প্রশ্ন \ ৩ \ দুইটি কোণ পরস্পর পূরক হলে এদের সমষ্টি কত?
(ক) ৩৬০° (খ) ১৮০° ✅ ৯০° (ঘ) ৮০°

প্রশ্ন \ ৪ \ ত্রিকোণীয় একটি কোণ ৪৫° হলে অপর বৃহত্তর কোণটি কত?
(ক) ৩৬০° (খ) ১৮০° ✅ ৯০° (ঘ) ৮০°

প্রশ্ন \ ৫ \ সম্পাদ্যের ক্ষেত্রে-
(i) যাহা দেওয়া থাকে তাহাই উপাত্ত
(ii) যাহা করণীয়, তাই অংকন
(iii) যুক্তি দ্বারা অংকন করা হলো প্রমাণ
নিচের কোনটি সঠিক?
(ক) i ও ii (খ) i ও iii (গ) ii ও iii ✅ i, ii ও iii

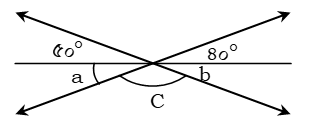
উপরের চিত্রের আলোকে (৬-৮) নং প্রশ্নের উত্তর দাও :
প্রশ্ন \ ৬ \ ∠a = কত?
(ক) ৩০° ✅ ৪০° (গ) ৫০° (ঘ) ৯০°

প্রশ্ন \ ৭ \ ∠a + ∠b = কত?
(ক) ৪০° (খ) ৫০° (গ) ৬০° ✅ ৯০°

প্রশ্ন \ ৮ \ ∠c = কত?
✅ ৯০° (খ) ১৩০° (গ) ১৬০° (ঘ) ১৮০°

প্রশ্ন \ ৯ \ চাঁদার সাহায্যে আঁকা যায়-
(i) ৪৫° ডিগ্রি কোণ
(ii) ১৫৫° কোণ
(iii) বৃত্ত
নিচের কোনটি সঠিক?
✅ i ও ii (খ) i ও iii (গ) ii ও iii (ঘ) i, ii ও iii

প্রশ্ন \ ১০ \ রুলারের সাহায্যে 8 সে.মি. দৈর্ঘ্যরে একটি রেখাংশ আঁক। এবার রুলার ও কম্পাসের সাহায্যে এই রেখাংশের সমান একটি রেখাংশ আঁক।
সমাধান :

বিশেষ নির্বচন : মনে করি, AB = ৪ সে.মি. দীর্ঘ একটি রেখাংশ। এর সমান করে একটি রেখাংশ আঁকতে হবে।
অঙ্কনের ধাপসমূহ :
১. যেকোনো রশ্মি CE নিই।
২. C কে কেন্দ্র করে AB এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি CE কে D বিন্দুতে ছেদ করে।
৩. তাহলে CD রেখাংশই AB রেখাংশের সমান রেখাংশ অঙ্কিত হলো।

প্রশ্ন \ ১১ \ রুলারের সাহায্যে 6 সে.মি. দৈর্ঘ্যরে একটি রেখাংশ আঁক। রুলার ও কম্পাসের সাহায্যে এই রেখাংশকে সমদ্বিখণ্ডিত কর। দ্বিখণ্ডিত রেখাংশ দুইটি মেপে দেখ তারা সমান হয়েছে কিনা।

সমাধান :

4

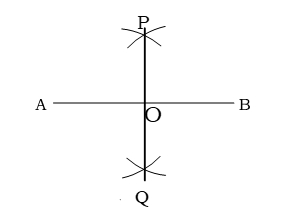
বিশেষ নির্বচন : প্রথমে একটি রুলার নিই। রুলারের সাহায্যে ৬ সে. মি. দীর্ঘ একটি রেখাংশ AB নিই। একে সমদ্বিখণ্ডিত করতে হবে।
অঙ্কনের ধাপসমূহ :
১. AB রেখাংশের A কে কেন্দ্র করে AB এর সমান বা অর্ধেকের বেশি ব্যাসার্ধ নিয়ে AB এর দুই পাশে দুইটি বৃত্তচাপ আঁকি।
২. B কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে AB এর দুই পাশে আরও দুইটি বৃত্তচাপ আঁকি। উভয় পাশের বৃত্তচাপ দুইটি P ও Q বিন্দুতে ছেদ করে।
৩. P, Q যোগ করি।
৪. PQ রেখাংশ AB রেখাংশকে O বিন্দুতে ছেদ করে। তাহলে, AB রেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হলো।
৫. রুলারের সাহায্যে মেপে দেখি OA ও OB রেখাংশের দৈর্ঘ্যরে সমান। অর্থাৎ OA = OB।

প্রশ্ন \ ১২ \ রুলারের সাহায্যে 8 সে.মি. দৈর্ঘ্যরে একটি রেখাংশ আঁক। রুলার ও কম্পাসের সাহায্যে এই রেখাংশকে সমান চার ভাগে ভাগ কর।
সমাধান :

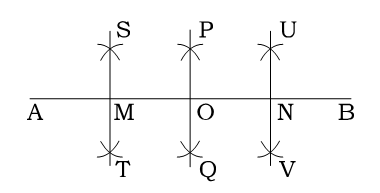
বিশেষ নির্বচন : রুলারের সাহায্যে ৪ সে.মি. দৈর্ঘ্যবিশিষ্ট একটি রেখাংশ AB আঁকি। একে সমান চার ভাগে বিভক্ত করতে হবে।
অঙ্কনের ধাপসমূহ :
১. রুলারের সাহায্যে ৪ সে.মি. দৈর্ঘ্যবিশিষ্ট একটি রেখাংশ AB আঁকি।
২. A কে কেন্দ্র করে AB এর সমান বা অর্ধেকের বেশি ব্যাসার্ধ নিয়ে AB এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি।
৩. B কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে AB এর উভয় পাশে আরও দুইটি বৃত্তচাপ আঁকি। উভয় পাশের বৃত্তচাপদ্বয় P এবং Q বিন্দুতে ছেদ করে।
৪. P, Q যোগ করি। PQ রেখাংশ AB রেখাংশকে O বিন্দুতে ছেদ করে।
৫. A কে কেন্দ্র করে AO এর সমান বা অর্ধেকের বেশি ব্যাসার্ধ নিয়ে AO এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি। B কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে OB এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি।
৬. O কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে OA এবং OB এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি। উক্ত বৃত্তচাপগুলো পরস্পর S, T, U, V বিন্দুতে ছেদ করল।
৭. S, T ও U, V যোগ করি। ST রেখাংশ AB কে M বিন্দুতে এবং UV রেখাংশ AB কে N বিন্দুতে ছেদ করল।
অতএব, AB রেখাংশটি M, O, N বিন্দুতে সমান চার অংশে বিভক্ত হলো। অর্থাৎ AM = OM = ON = NB

প্রশ্ন \ ১৩ \ 7 সে.মি. দৈর্ঘ্যরে রেখাংশের মধ্যবিন্দুতে রুলার-কম্পাসের সাহায্যে একটি নির্দিষ্ট লম্ব আঁক।
সমাধান :

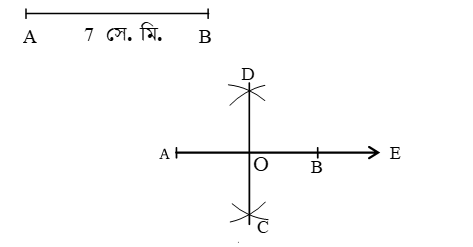
বিশেষ নির্বচন : মনে করি, ৭ সে.মি. দৈর্ঘ্যরে সমান AB একটি রেখাংশ। উক্ত রেখাংশের মধ্যবিন্দুতে লম্ব আঁকতে হবে।
অঙ্কনের ধাপসমূহ :
১. যেকোনো একটি রেখাংশ AE নিই। AE হতে ৭ সে.মি. এর সমান করে AB অংশ কেটে নিই।
২. A বিন্দুকে কেন্দ্র করে AB এর অর্ধেকের বেশি ব্যাসার্ধ নিয়ে
AB এর দুইপাশে দুইটি বৃত্তচাপ আঁকি।
৩. আবার, B বিন্দুকে কেন্দ্র করে একই ব্যাসার্ধ নিয়ে AB এর উভয় পাশে আরও দুইটি বৃত্তচাপ আঁক। এরা পূর্বের বৃত্তচাপ দুইটিকে
C ও D বিন্দুতে ছেদ করে।
৪. C, D যোগ করি।
৫. CD রেখা AB রেখাংশকে O বিন্দুতে ছেদ করে। তাহলে OD রেখাংশ AB রেখাংশের মধ্যবিন্দুতে লম্ব অঙ্কিত হলো। অর্থাৎ OD ⊥ AB.

প্রশ্ন \ ১৪ \ ৮ সে.মি. দৈর্ঘ্যরে রেখাংশের মধ্যবিন্দুতে লম্ব আঁক।
সমাধান :

বিশেষ নির্বচন : মনে করি, AB = ৮ সে.মি. একটি রেখাংশ। এর মধ্যবিন্দুতে একটি লম্ব আঁকতে হবে।
অঙ্কনের ধাপসমূহ :
১. যেকোনো একটি রেখাংশ AE নিই। AE হতে ৮ সে.মি. এর সমান করে AB অংশ কেটে নিই।
২. A বিন্দুকে কেন্দ্র করে AB এর অর্ধেকের বেশি ব্যাসার্ধ নিয়ে AB এর দুইপাশে দুইটি বৃত্তচাপ আঁকি।
৩. আবার, B বিন্দুকে কেন্দ্র করে একই ব্যাসার্ধ নিয়ে AB এর উভয় পাশে আরও দুইটি বৃত্তচাপ আঁক। এরা পূর্বের বৃত্তচাপ দুইটিকে C ও D বিন্দুতে ছেদ করে।
৪. C, D যোগ করি।
৫. CD রেখা AB রেখাংশকে O বিন্দুতে ছেদ করে। তাহলে OD রেখাংশ AB রেখাংশের মধ্যবিন্দুতে লম্ব অঙ্কিত হলো। অর্থাৎ OD ⊥ AB.

প্রশ্ন \ ১৫ \ AB সরলরেখার C বিন্দুতে CD লম্ব আঁক। আবার CD রেখার উপর একটি বিন্দু E লও। এবার E বিন্দুতে CD রেখার উপর লম্ব আঁক।
সমাধান :

বিশেষ নির্বচন : দেওয়া আছে, AB রেখার অন্তঃস্থ C একটি বিন্দু। AB রেখার C বিন্দুতে CD লম্ব আঁকতে হবে। আবার, CD রেখার উপর একটি বিন্দু E নিই। এবার E বিন্দুতে CD রেখার উপর লম্ব আঁকতে হবে।
অঙ্কনের ধাপসমূহ :
১. যেকোনো একটি রেখাংশ AB এর উপর C একটি বিন্দু লই।
২. C কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা AB রেখাংশকে P একটি ছেদ করে।
৩. P কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা আগের বৃত্তচাপকে Q বিন্দুতে ছেদ করে।
৪. আবার, Q কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে আরও একটি বৃত্তচাপ আঁকি যা আগের বৃত্তচাপকে R বিন্দুতে ছেদ করে।
৫. Q ও R কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একই দিকে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুইটি পরস্পর S বিন্দুতে ছেদ করে।
৬. C, S যোগ করে D পর্যন্ত বর্ধিত করি। অতএব, CD ⊥ AB.
৭. অনুরূপভাবে, CD রেখার E বিন্দুতে EF লম্ব আঁকি।
৮. AB রেখার C বিন্দুতে CD এবং CD রেখার E বিন্দুতে EF লম্ব অঙ্কিত হলো।
অর্থাৎ CD ⊥ AB এবং EF ⊥ CD.

প্রশ্ন \ ১৬ \ চাঁদা ব্যবহার না করে ৪৫° কোণটি আঁক।
সমাধান : চাঁদা ব্যবহার না করে ৪৫° কোণটি আঁকতে হবে।

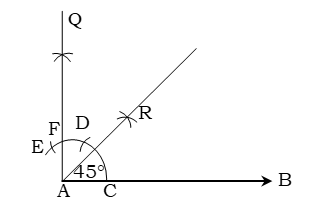
অঙ্কনের ধাপসমূহ :
১. যেকোনো রেখাংশ AB নিই।
২. A বিন্দুকে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি, বৃত্তচাপটি AB কে C বিন্দুতে ছেদ করে।
৩. C কে কেন্দ্র করে একই ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি, যা আগের বৃত্তচাপকে D বিন্দুতে ছেদ করে।
৪. আবার D বিন্দুকে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে আরও একটি বৃত্তচাপ আঁকি। এ বৃত্তচাপটি আগের বৃত্তচাপকে E বিন্দুতে ছেদ করে।
৫. D ও E কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একই দিকে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুইটি পরস্পর Q বিন্দুতে ছেদ করে।
৬. A,Q যোগ করি। AQ, ED বৃত্তচাপকে F বিন্দুতে ছেদ করে। তাহলে, AQ ⊥ AB এবং ∠BAQ = ৯০°
৭. C ও F কে কেন্দ্র করে CF এর অর্ধেকের বেশি ব্যাসার্ধ নিয়ে ∠BAQ এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পর
R বিন্দুতে ছেদ করে।
৮. A, R যোগ করি। AR রেখাংশ ∠BAQ এর সমদ্বিখণ্ডক। অর্থাৎ, ∠BAR ও ∠QAR কোণের প্রত্যেকের মান ৪৫° হবে।

প্রশ্ন \ ১৭ \ ABC ত্রিভুজের তিনটি কোণের সমদ্বিখণ্ডকগুলো আঁক। যে রেখাগুলো দ্বারা কোণগুলো সমদ্বিখণ্ডিত হয়েছে ঐ রেখাগুলোর সাধারণ বিন্দু চিহ্নিত কর।
সমাধান :

বিশেষ নির্বচন : মনে করি, ABC একটি ত্রিভুজ। এর ∠ABC, ∠BCA ও ∠BAC এর প্রত্যেকটিকে সমদ্বিখণ্ডিত করতে হবে। যে রেখাগুলো দ্বারা কোণগুলো সমদ্বিখণ্ডিত হয়েছে ঐ রেখাগুলোর সাধারণ বিন্দু চিহ্নিত করতে হবে।
অঙ্কনের ধাপসমূহ :
১. ABC ত্রিভুজের B কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি। এই বৃত্তচাপটি AB ও BC কে P ও Q বিন্দুতে ছেদ করল।
২. P ও Q কে কেন্দ্র করে PQ এর সমান অথবা অর্ধেকের চেয়ে বেশি ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে আরও দুইটি বৃত্তচাপ আঁকি। এই বৃত্তচাপদ্বয় পরস্পর R বিন্দুতে ছেদ করে।
৩. B, R যোগ করে E পর্যন্ত বর্ধিত করি। এই BE রেখাই ∠ABC এর সমদ্বিখণ্ডক।
৪. অনুরূপভাবে, ∠ACB ও ∠BAC কে CF ও AD রেখা দ্বারা সমদ্বিখণ্ডিত করা হলো।
৫. সমদ্বিখণ্ডিত AD, BE ও CF রেখাত্রয় পরস্পর O বিন্দুতে মিলিত হয়েছে।
সুতরাং O বিন্দুই হলো সমদ্বিখণ্ডক রেখাত্রয়ের সাধারণ বিন্দু।

প্রশ্ন \ ১৮ \ পাশের চিত্রে,

ক. ∠ABC এর সম্পূরক কোণ কোনটি?
খ. ∠ACB এর মান কত এবং কেন?
গ. প্রমাণ কর যে, ∠DCE + ∠ECB = ১৮০°.

সমাধান :
ক. দেওয়া আছে, ∠ABC = ৫০°
আমরা জানি, দুইটি কোণের সমষ্টি ১৮০° হলে কোণদ্বয়ের একটিকে অপরটির সম্পূরক কোণ বলে। চিত্রে ∠ABC এর সম্পূরক কোণ হলো ∠CBF.

খ. ∠ACB এর মান হলো ৫০°
কারণ: দেওয়া আছে, ∠DCE = ৫০°
এখানে AE রেখাংশ এবং BD রেখাংশ পরস্পরকে C বিন্দুতে ছেদ করে এবং বিপ্রতীপ কোণ উৎপন্ন করে। বিপ্রতীপ কোণসমূহ হলো ∠DCE এবং ∠ACB.
বিপ্রতীপ কোণসমূহ পরস্পর সমান তাই ∠DCE = ∠ACB
যেহেতু ∠DCE = ৫০°
সুতরাং ∠ACB = ৫০° হবে।

গ. প্রমাণ করতে হবে যে, ∠DCE + ∠ECB = ১৮০°
প্রমাণ : দেওয়া আছে, ∠DCE = ৫০°
চিত্র হতে দেখা যায়,
∠DCB = ∠DCE + ∠ECB
বা, ১৮০° = ৫০° + ∠ECB [∠DCB সরল কোণ বলে]
বা, ∠ECB = ১৮০° – ৫০°
∴ ∠ECB = ১৩০°
∴ ∠DCE + ∠ECB = ৫০° + ১৩০° = ১৮০° (প্রমাণিত)

 

প্রশ্ন \ ১৯ \ পাশের চিত্রে,

ক. ∠AOB এর বিপ্রতীপ কোণ কোনটি?
খ. ∠AOB কে সমদ্বিখণ্ডিত করে সন্নিহিত কোণ দুইটির সাধারণ বাহু নির্দেশ কর।
গ. প্রমাণ কর যে, ∠AOB এবং ∠COD এর সমদ্বিখণ্ডক একই সরলরেখায় অবস্থিত।

সমাধান :
ক.

আমরা জানি, কোনো কোণের বাহুদ্বয়ের বিপরীত রশ্মি দুইটি যে কোণ উৎপন্ন করে, তাকে ঐ কোণের বিপ্রতীপ কোণ বলে।
যেহেতু ∠AOB এর AO ও BO বাহুদ্বয়ের বিপরীত রশ্মি DO ও CO পরস্পর মিলিত হয়ে ∠COD উৎপন্ন করে। তাই ∠AOB এর বিপ্রতীপ কোণ ∠COD।

খ. চিত্রে ∠AOB কে OE রেখা দ্বারা সমদ্বিখণ্ডিত করা হলো:

এখানে ∠AOE এবং ∠BOE দুইটি সন্নিহিত কোণ।
আমরা জানি, সন্নিহিত কোণদ্বয়ের একটি সাধারণ বাহু থাকে এবং কোণদ্বয় সাধারণ বাহুর বিপরীত পাশে অবস্থান করে।
সুতরাং ∠AOE এবং ∠BOE এর সাধারণ বাহু OE।

গ.

∠AOB এর সমদ্বিখণ্ডক OE এবং ∠COD এর সমদ্বিখণ্ডক OF. প্রমাণ করতে হবে যে, OE এবং OF একই সরলরেখায় অবস্থিত।
প্রমাণ : OE, ∠AOB এর সমদ্বিখণ্ডক।
∴ ∠AOE = ∠BOE
∴ ∠AOB = ∠AOE + ∠BOE [∵AOE = ∠BOE]
= ∠AOE + ∠AOE = ২∠AOE

আবার, OF, ∠DOC এর সমদ্বিখণ্ডক।
∴ ∠DOF = ∠COF
∴ ∠COD = ∠DOF + ∠COF
= ∠COF + ∠COF [∵DOF = ∠COF]
= ২ ∠COF

এখন ∠AOB = ∠COD [বিপ্রতীপ কোণ বলে]
বা, ২∠AOE = ২∠COF
বা, ∠AOE = ∠COF
∠AOE = ∠COF কোণ দুইটি বিপ্রতীপ কোণ।
∴ EF একই সরলরেখা।
∴OE ও OF সমদ্বিখণ্ডকদ্বয় একই সরলরেখায় অবস্থিত। (প্রমাণিত)

প্রশ্ন \ ২০ \ চিত্রে ∠ABC = ৯০°

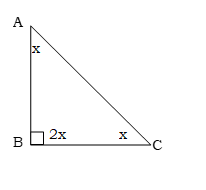
ক. ত্রিভুজের তিনটি কোণের সমষ্টিকে X এর মাধ্যমে প্রকাশ কর।
খ. ∠ABC কে সমদ্বিখণ্ডিত কর এবং অংকনের বিবরণ দাও।
গ. X কোণের সমান করে একটি কোণ আঁক এবং বিবরণ দাও।

সমাধান :
ক) চিত্রানুযায়ী,
ΔABC -এ ∠ABC = 2X, ∠ACB = X এবং ∠BAC = X
∴ ∠ABC + ∠ACB + ∠BAC = 2X + X + X = ৪X

উত্তর : ৪X

খ)

দেওয়া আছে, ΔABC এ ∠ABC একটি নির্দিষ্ট কোণ। কোণটিকে সমদ্বিখণ্ডিত করতে হবে।
অঙ্কনের বিবরণ :
১। B বিন্দুকে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি AB ও BC রেখাকে যথাক্রমে Q ও P একটি ছেদ করে।
২। P কে কেন্দ্র করে PQ এর অর্ধেকের চেয়ে বেশি ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে একটি বৃত্তচাপ আঁকি।
৩। Q বিন্দুকে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে অপর একটি বৃত্তচাপ আঁকি। ঐ বৃত্তচাপটি আগের বৃত্তচাপকে D বিন্দুতে ছেদ করে।
৪। B, D যোগ করি।
তাহলে, BD রেখাংশ ∠ABC এর সমদ্বিখণ্ডক।

গ) ‘ক’ থেকে পাB,
ΔABC এর তিন কোণের সমষ্টি = ৪X
∴ ৪X = ১৮০°
বা, X = ১৮০°/৪
∴ X = ৪৫°

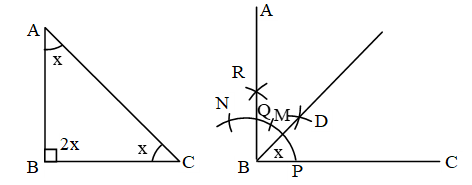
ΔABC-এ ∠X = ৪৫°। এর সমান একটি কোণ আঁকতে হবে।

অঙ্কনের বিবরণ :
১। BC রেখার B বিন্দুকে কেন্দ্র করে সুবিধামতো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা BC কে P একটি ছেদ করে।
২। P কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা আগের বৃত্তচাপকে M বিন্দুতে ছেদ করে। আবার M কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা প্রথমে আঁকা বৃত্তচাপকে N বিন্দুতে ছেদ করে।
৩। M ও N কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে একই দিকে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুইটি R বিন্দুতে ছেদ করে।
৪। B, R যোগ করে A পর্যন্ত বর্ধিত করি। BR রেখা প্রথম বৃত্তচাপকে Q বিন্দুতে ছেদ করে।
৫। P ও Q কে কেন্দ্র করে PQ এর অর্ধেকের বেশি ব্যাসার্ধ নিয়ে একই দিকে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে D বিন্দুতে ছেদ করে। B, D যোগ করি।
তাহলে, ∠DBC = ∠ABD = ∠X অঙ্কিত হলো।

---

আরো পড়ুনঃ

🔶🔶 ৬ষ্ঠ শ্রেণির গণিত সমাধান

🔶🔶 ৬ষ্ঠ শ্রেণির সকল বিষয় সমাধান