সপ্তম/ ৭ম শ্রেণির গণিত অনুশীলনী ৯.২ এর সমাধান পোস্টে সকল কে স্বাগতম। এখানে সপ্তম শ্রেণির গণিতের শুধুমাত্র অনুশীলনী ৯.২ এর সমাধান দেওয়া হয়েছে। সপ্তম শ্রেণির সকল বিষয়ের সমাধান পেতে নিচে দেওয়া লিংকে প্রবেশ করুন।

সপ্তম শ্রেণির গণিত অনুশীলনী ৯.২

নিচের তথ্যের ভিত্তিতে 1-3 নম্বর প্রশ্নের উত্তর দাও :

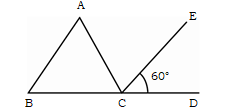
চিত্রে, CE, ∠ACD এর সমদ্বিখণ্ডক। AB \ CE এবং ∠ECD = 60°
প্রশ্ন \ 1 \ ∠BAC এর মান নিচের কোনটি?
ক. 30° খ. 45° গ. 60°✅ ঘ. 120°
ব্যাখ্যা : যেহেতু AB \ CE এবং AC ছেদক
∴ ∠BAC = ∠ACE [একান্তর কোণ]
কিন্তু CE, ∠ACD এর সমদ্বিখণ্ডক।
সুতরাং ∠ACE = ∠ECD = 60°
∴ ∠BAC = 60°

প্রশ্ন \ 2 \ ∠ACD এর মান নিচের কোনটি?
ক. 60° খ. 90° গ.120°✅ ঘ. 180°
ব্যাখ্যা : ∠ACD = ∠ACE + ∠ECD = 60° + 60° = 120°

প্রশ্ন \ 3 \ ΔABC কোন ধরনের ত্রিভুজ?
ক. স্থূলকোণী খ. সমদ্বিবাহু গ. সমবাহু✅ ঘ. সমকোণী

ব্যাখ্যা : যেহেতু BA \ CE এবং BD ছেদক
∴ ∠ABC = ∠ECD = 60° [অনুরূপ কোণ]
আবার, ∠BAC + ∠ABC + ∠ACB = 180°
বা, 60° + 60° + ∠ACB = 180°
বা, ∠ACB = 180° – 120° = 60°
∴ ∠ACB = 60°
সুতরাং ∠BAC = ∠ABC = ∠ACB = 60°
অতএব, ΔABC সমবাহু

প্রশ্ন \ ৪ \ একটি ত্রিভুজের দুইটি বাহু যথাক্রমে 5 সে.মি. এবং 4 সে.মি. ত্রিভুজটির অপর বাহুটি নিচের কোনটি হতে পারে?
ক. 1 সে.মি. গ. 4 সে.মি.✅ গ. 9 সে.মি. ঘ. 10 সে.মি.
ব্যাখ্যা : 5 সে.মি. + 4 সে.মি. = 9 সে.মি. > 4 সে.মি.

প্রশ্ন \ ৫ \ সমকোণী ত্রিভুজের সূক্ষকোণদ্বয়ের একটি 40° হলে, অপর সূক্ষকোণের মান নিচের কোনটি?
ক. 40° খ. 45° গ. 50°✅ ঘ. 60°
ব্যাখ্যা : অপর সূক্ষকোণ = 90° – 40° = 50°

প্রশ্ন \ 6 \ কোনো ত্রিভুজের একটি কোণ অপর দুইটি কোণের সমষ্টির সমান হলে, ত্রিভুজটি কী ধরনের হবে?
ক. সমবাহু খ. সূক্ষকোণী গ. সমকোণী✅ ঘ. স্থূলকোণী

প্রশ্ন \ 7 \ ΔABC-এ AB > AC এবং ∠B ও ∠C এর সমদ্বিখণ্ডকদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, PB > PC.
সমাধান :

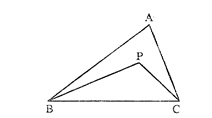
বিশেষ নির্বচন : মনে করি, ΔABC এ AB > AC এবং ∠B ও ∠C এর সমদ্বিখণ্ডকদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে।
প্রমাণ কর যে, PB > PC.
প্রমাণ :
ধাপ যথার্থতা
1. ΔABC -এ AB > AC [কল্পনা]
∴ ∠ACB > ∠ABC [ত্রিভুজের বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর]
∴1/2 ∠ACB > 1/2 ∠ABC. [ উভয়পক্ষকে 12 দ্বারা গুণ করে ]
বা, ∠PCB >∠PBC [PB ও PC যথাক্রমে ∠ABC এবং ∠ACB এর সমদ্বিখণ্ডক]
2. ΔPBC -এ ∠PCB >∠PBC
∴ PB > PC. [প্রমাণিত] [বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর]

প্রশ্ন \ 8 \ ABC একটি সমদ্বিবাহু ত্রিভুজ এবং এর AB = AC; BC কে যেকোনো দূরত্বে উ পর্যন্ত বাড়ানো হলো। প্রমাণ কর যে, AD > AB.
সমাধান :

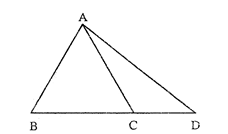
বিশেষ নির্বচন : মনে করি, ΔABC-এ AB = AC; BC কে যেকোনো দূরত্বে উ পর্যন্ত বাড়ানো হলো। প্রমাণ করতে হবে যে, AD > AB.
প্রমাণ :
ধাপ: যথার্থতা
1. ΔABC-এ AB = AC [কল্পনা]
∴ ∠ABC = ∠ACB [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণদ্বয় পরস্পর সমান]
2. ΔADC-এর বহিঃস্থ ∠ACB
∴ ∠ACB > ∠ADC [ত্রিভুজের বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের প্রত্যেকটি অপেক্ষা বৃহত্তর]
3. ΔABD-এ ∠ABD >∠ADB [ত্রিভুজের বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর]
∴ AD > AB. [প্রমাণিত]

প্রশ্ন \ 9 \ ABCD চতুর্ভুজে AB = AD, BC = CD এবং CD > AD. প্রমাণ কর যে, ∠DAB >∠BCD.
সমাধান :

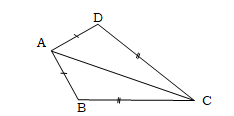
মনে করি, ABCD চতুর্ভুজে AB = AD, BC = CD এবং CD > AD. প্রমাণ করতে হবে যে, ∠DAB > ∠BCD.
অঙ্কন : A, C যোগ করি।
প্রমাণ :
ধাপ                                   যথার্থতা
1. ΔADC -এ CD > AD [কল্পনা]
∴ ∠DAC > ∠DCA [ত্রিভুজের বৃহত্তর বাহুর বিপরীত
কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর]
2. ΔABC -এ BC > AB [CD = BC এবং AD = AB]
∴ ∠BAC > ∠BCA [1 নং অনুসারে]
3. ∠DAC + ∠BAC > ∠DAC + ∠BCA
[ উভয়পক্ষে ∠DAC যোগ করে]
বা, ∠DAC + ∠BAC > ∠DCA + ∠BCA [∵ ∠DAC > ∠DCA ]
∴ ∠DAB > ∠BCD [প্রমাণিত]

১০. △ABC এ ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।

(ক) তথ্যের আলোকে চিত্রটি অঙ্কন কর।

(খ) দেখাও যে, AC>AB
(গ) প্রমান কর যে, AB+AC>2AD

সমাধানঃ

(ক)
প্রদত্তের আলোকে নিচের চিত্রটি আঁকা হলোঃ-

(খ)
△ABC এ ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।
দেখাতে হবে যে, AC>AB
প্রামানঃ
যদি AC>AB না হয় তবে AC=AB বা AC<AB হবে।
AC=AB হলে, ∠ABC=∠ACB হবে [কারন সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান হয়]
কিন্তু, ∠ABC>∠ACB বিধায় AC=AB হবে না।
আবার,
AC<AB হলে, ∠ABC<∠ACB হবে [কারন ক্ষুদ্রতর বাহুর বিপরীত কোণ ক্ষুদ্রতর হয়]
কিন্তু, ∠ABC>∠ACB বিধায় AC<AB হবে না।
তাহলে, AC>AB হবে (দেখানো হলো)
(গ)

বিশেষ নির্বাচনঃ
△ABC এ ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।
প্রমান করতে হবে যে, AB+AC>2AD.

অঙ্কনঃ

AD কে E পর্যন্ত এমন ভাবে বর্ধিত করি যেন AD=DE হয়। এবং E, C যোগ করি।
প্রমাণঃ
△ABD ও △DEC-এর ক্ষেত্রে,
AD=DE [অঙ্কনানুসারে]
BD=DC [প্রশ্নানুসারে]
∠ADB=∠EDC [বিপ্রতীপ কোন]
∴△ABD ≅ △DEC
∴AB=EC
এখন,
△AEC-এর ক্ষেত্রে,
AC+EC>AE
বা, AC+AB>AD+DE [∴AB=EC]
বা, AC+AB>2AD (প্রমাণিত)

প্রশ্ন \ 11 \ ΔABC-এ AB = AC এবং D, BC-এর উপর একটি বিন্দু।প্রমাণ কর যে, AB > AD.
সমাধান :

বিশেষ নির্বচন : মনে করি, ΔABC -এ AB = AC এবং D, BC-এর উপর একটি বিন্দু। A, D যোগ করি। প্রমাণ করতে হবে যে, AB > AD.
প্রমাণ :
ধাপ যথার্থতা
1. ΔABC-এ AB = AC
∴ ∠ABC = ∠ACB . [সমান বাহুর বিপরীত কোণদ্বয় সমান]
2. ΔADC-এর বহিঃস্থ ∠ADB > ∠ACD [ত্রিভুজের বহিঃস্থ কোণ অন্তঃস্থ বিপরীত
কোণদ্বয়ের প্রত্যেকটি অপেক্ষা বৃহত্তর]
বা, ∠ADB > ∠ACB .
বা, ∠ADB > ∠ABC. [1 নং হতে]
বা, ∠ADB > ∠ABD.
3. ΔABD-এ ∠ADB>∠ABD.
∴ AB > AD. [প্রমাণিত] [ত্রিভুজের বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর]

প্রশ্ন \ 12 \ ΔABC -এ AB ⊥ AC এবং D, AC-এর উপর একটি বিন্দু। প্রমাণ কর যে, BC > BD.
সমাধান :

মনে করি, ΔABC -এ AB ⊥ AC এবং D, AC-এর উপর একটি বিন্দু। B, D যোগ করি। প্রমাণ করতে হবে যে, BC > BD.
প্রমাণ :
ধাপ যথার্থতা
1. ΔABD-এ ∠BAD = 90° [AB ⊥ AC]
এবং ∠ACB < 90° [∠ACB + ∠ABC = 90°]
∴ ∠BAD > ∠ACB .
2. ΔABD-এর বহিঃস্থ ∠BDC > ∠BAD. [ত্রিভুজের বহিঃস্থ কোণ এর অন্তঃস্থ বিপরীত কোণ অপেক্ষা বৃহত্তর]
3. ΔBDC-এ ∠BDC >∠BCD. [1 এবং 2 হতে]
∴ BC > BD. [প্রমাণিত] [ত্রিভুজের বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর।]

প্রশ্ন \ 13 \ প্রমাণ কর যে, সমকোণী ত্রিভুজের অতিভুজই বৃহত্তম বাহু।
সমাধান :

মনে করি, ΔABC-এ AB ও BC সমকোণী সংলগ্ন দুইটি বাহু এবং AC অতিভুজ। প্রমাণ করতে হবে যে, AC > AB এবং AC > BC.
প্রমাণ :
ধাপ যথার্থতা
1. ΔABC-এ ∠ABC > ∠ACB [ ∠ABC = 90° এবং ∠ACB < 90°]
∴ AC > AB [ত্রিভুজের বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর]
2. ∠ABC > ∠BAC
AC > BC
∴ AC-ই বৃহত্তম বাহু
অর্থাৎ, অতিভুজই ত্রিভুজটির বৃহত্তম বাহু। [প্রমাণিত]

প্রশ্ন \ 14 \ প্রমাণ কর যে, ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম।
সমাধান :

মনে করি, ΔABC -এ BC বাহু বৃহত্তম। প্রমাণ করতে হবে যে, ∠BAC বৃহত্তম কোণ।
প্রমাণ :
ধাপ যথার্থতা
1. ΔABC-এ BC > AB [BC বৃহত্তর বাহু]
∴ ∠BAC >∠ACB . [বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর]
2. আবার BC > AC [কল্পনা]
∴ ∠BAC > ∠ABC [বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর
বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর]
∴ ∠BAC-ই বৃহত্তম কোণ। [প্রমাণিত]

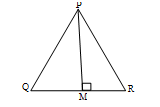
প্রশ্ন \ 15 \ চিত্রে, ∠QPM =∠RPM এবং ∠QPR = 90°
ক) ∠QPM এর মান নির্ণয় কর।
খ) ∠PQM ও ∠PRM এর মান কত?
গ) PQ = 6 সে.মি. হলে, PR এর মান নির্ণয় কর।

সমাধান:

ক) চিত্রানুসারে,
∠QPM +∠RPM = ∠QPR =90°
বা, ∠QPM +∠QPM = 90° [∠QPM =∠RPM]
বা, 2∠QPM = 90°
∴ ∠QPM = 90°2 = 45°
খ) ΔPQM-এ ∠PMQ = 90° [PM ⊥ QR]
∠QPM = 45° [ ক নং হতে ]
∴ ∠PQM + ∠QPM = 90°
বা, ∠PQM + 45° = 90°
বা, ∠PQM = 90°- 45° = 45°
আবার, ∠RPM = ∠QPM = 45°, ∠PMR = 90°
∴ ∠PRM = 90°- 45° = 45°
গ) ΔPQR এ ∠PQR = ∠PRQ [∵ প্রত্যেকেই 45° এর সমান]
∴ PQ = PR [ত্রিভুজের সমান সমান কোণের বিপরীত বাহু সমান]
∴ PR = 6 সে.মি. [∵ PQ = 6 সে.মি.]

আরো পড়ুনঃ

🔶🔶 ৭ম শ্রেণির গণিত সমাধান

🔶🔶 ৭ম শ্রেণির সকল বিষয় সমাধান