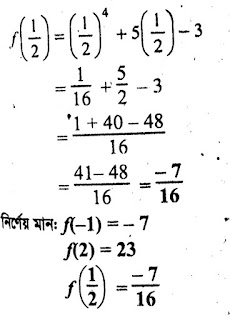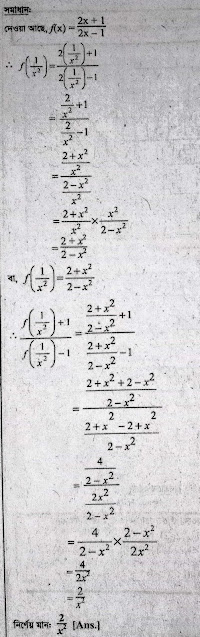এসএসসি সাধারণ গণিত অনুশীলনী ২.২ সেট ফাংশন প্রশ্ন সমাধান [ ssc math chapter 2.2 set and function question & answer ]
নমব, দশম, অথবা এসএসসি শিক্ষার্থী সাধারণ গণিতের অনুশীলনীর অনেক সমস্যার সমাধান তাদের গাইড বইয়ে পাওয়া যায় না। কারণ অনেকে সাধারণ গণিত পুরাতন গাইড ব্যবহার করে। আবার একজন শিক্ষকের কাছেও এরকমটা হতে পারে। তাই সাধারণ গণিতের সেট ফাংশন অধ্যায়ের প্রশ্নগুলোর উত্তর সঠিক ও নির্ভূলভাবে দেওয়া হলো।
আপনারা গণিত অনুশীলনী ২.২ সমাধান এর পিডিএফ কপি নিতে চাইলে নিচে কমেন্ট করুন।
সাধারণ গণিত অনুশীলনী ২.২ সেট ফাংশন
১। ৪ এর গুণনীয়ক সেট কোনটি?
ক) {8,16,24,—} খ) {1,2,4, 8}
গ) {2,4, 8} ঘ) {1,2}
উত্তরঃ খ
২। সেট C হতে সেট B এ একটি সম্পর্ক R হলে নিচের কোনটি সঠিক?
ক) R ⊂ C খ) R ⊂ B
গ) R ⊆ C × B ঘ) C × B ⊆ R
উত্তরঃ গ
৩। A= {1,2}, B = (2,5) হলে P(A∩B) এর সদস্য সংখ্যা নিচের কোনটি?
ক) 1 খ) 2 গ) 3 ঘ) ৪
উত্তরঃ খ
৪। নিচের কোনটি {x ∈ N : 13 <x <17 এবং x মৌলিক সংখ্যা} সেটটিকে তালিকা পদ্ধতিতে
প্রকাশ করে?
ক) ∅ খ) {0} গ) {∅} ঘ) {13,17)}
উত্তরঃ ক
৫। A∪B= {a,b,c} হলে
- (i) A= {a,b}, B= {a,b,c}
- (ii) A= {a,b,c}, B = {b,c}
- (iii) A = {a,b}, B= {c}
উপর্যুন্ত তথ্যের আলোকে নিচের কোনটি সঠিক?
ক) i খ) ii A) i ও ii ঘ) i, ii ও iii
উত্তরঃ ঘ
৬। A ও B দুইটি সসীম সেটের জন্য
- (i) A×B = {x,y):x∈A এবং y∈B}
- (ii) n(A) = a,n(B) = b হলে n(A × B) = ab
- (iii) A × B এর প্রতিটি সদস্য একটি ক্রমজোড়
উপর্যুন্ত তথ্যের আলোকে নিচের কোনটি সঠিক?
ক) i খ) ii A) i ও ii ঘ) i, ii ও iii
উত্তরঃ ঘ
A = {6,7,8,9,10,11,12,13) হলে, নিচের ৭ – ৯ প্রশ্নগুলোর উত্তর দাও:
৭। A সেটের সঠিক প্রকাশ কোনটি?
ক) {x ∈ N : 6 <x <13}
খ) {x ∈ N : 6 ≤ x < 13 }
গ) {x ∈ N : 6 ≤ x ≤ 13 }
ঘ) {x ∈ N : 6 < x ≤ 13 }
উত্তরঃ গ
৮। A সেটের মৌলিক সংখ্যাগুলোর সেট কোনটি?
ক) {6,8,10,12} খ) {7,9,11,13) গ) {7,11,13} ঘ) {9,12}
উত্তরঃ গ
৯। A সেটের 3 এর গুণিতকগুলোর সেট কোনটি?
ক) {6,9} খ) {6,11} গ) {9,12} ঘ) {6,9, 12}
উত্তরঃ ঘ
১০। যদি A= (3,4}, B= {2,4}, x ∈ A এবং y ∈ B হয়, তবে A ও B এর উপাদানগুলোর
মধ্যে x >y সম্পর্ক বিবেচনা করে অন্বয়টি নির্ণয় কর।
সমাধানঃ দেওয়া আছে,
A= (3,4}, B= {2,4}
প্রশ্নমতে, রিলেশনটি, R= {(x,y): x ∈ A এবং y ∈ B এবংx >y}
এখানে A×B = {3,4} ×{2,4}
={(3,2), (3,4), (4,2), (4,4)}
∴ x >y সম্পর্ক অনুসারে R = {(3,2), (4,2)} (ans)
১১। যদি C = {2,5},D = {4,6,7}, x ∈ C এবং y ∈ D হয় তবে C ও D এর উপাদানগুলোর মধ্যে x+1<y সম্পর্কটি বিবেচনায় থাকে তবে অন্বয়টি নির্ণয় কর।
সমাধানঃ দেওয়া আছে,
C = {2,5},D = {4,6,7}
প্রশ্নমতে, রিলেশনটি, R= {(x,y): x ∈ C এবং y ∈ D এবং x +1<y}
এখানে C×D = {2,5} ×{4,6,7}
={(2,4), (2,6), (2,7), (5,4), (5,6), (5,7)}
∴ x +1<y সম্পর্ক অনুসারে R ={(2,4), (2,6), (2,7), (5,7)} (ans)
১২। f(x) = x⁴ + 5x -3 হলে f(-1), f(2) এবং f(1/2) এর মান নির্ণয় কর।
সমাধানঃ
দেওয়া আছে, f(x) = x⁴ + 5x -3
∴ f(-1) = (-1)⁴ + 5(-1) -3
= 1-5-3
= -7 (ans)
f(x) = x⁴ + 5x -3
f(2) = 2⁴ + 5.2 -3
= 16+10-3
= 23 (ans)
f(x) = x⁴ + 5x -3
১৩। যদি f(y) = y³ + ky² – 4y — 8 হয়, তবে k এর কোন মানের জন্য f(-2) = 0 হবে?
সমাধানঃ দেওয়া আছে,
f(y) = y³ + ky² – 4y — 8
∴ f(-2) = (-2)³ + k(-2)² – 4(-2) — 8
= -8 +4k +8 — 8
=4k-8
আবার, f(-2) = 0 হবে যদি,
4k-8=০
বা, k= 8/4
∴ k=2
∴ k এর মান 2 হলে f(-2) = 0 হবে [ans]
১৪।. f(x) = x³ — 6x² + 11x – 6 হয়, তবে x এর কোন মানের জন্য f(2) = 0 হবে?
সমাধানঃ দেওয়া আছে,
f(x) = x³ — 6x² + 11x – 6
এখানে, f(2) = 0
বা, x³ — 6x² + 11x – 6 =0
বা, x³ – x² – 5x² + 5x + 6x – 6 =0
বা, x²(x-1) -5x(x-1) +6(x-1) = 0 [x=1 হলে সমীকরণটির মান শূন্য হয় তাই (x-1) এর একটি উৎপাদক]
বা, (x-1)(x²-5x+6) = 0
হয়, x-1=০
∴ x =1
অথবা, x²-5x+6 =0
বা, x²-2x – 3x+6 =0
বা, x(x-2)-3(x-2) =0
বা, (x-2)(x-3) =0
হয়, x-2 =0
∴ x =2
অথাব, x-3 =0
∴ x =3
x এর নির্ণেয় মানঃ1 অথবা 2 অথবা 3 [ans]
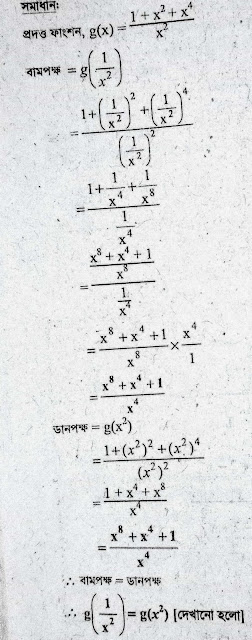
১৬ নং প্রশ্নের সমাধান
১৭। নিচের অন্বয়গুলো থেকে ডোমেন এবং রেঞ্জ নির্ণয় কর।
ক) R= {(2, 1), (2,2), (2, 3)}
খ) S = {(-2, 4),(-1, 1), (0,0), (1, 1), (2,4)}
গ) F={(1/2.0), (1,1), (1,-1), (5/2,2), (5/2, -2)}
(ক) এর সমাধানঃ দেওয়া আছে, R = {(2, 1), (2,2), (2, 3)}
R অন্বয়ের ক্রমজোড়গুলোর প্রথম উপাদানসমূহ 2, 2, 2 এবং দ্বিতীয় উপাদানসমূহ 1, 2,3
∴ ডোমেন R= {2} এবং রেন্জ R= {1,2,3} [ans]
(খ) এর সমাধানঃ দেওয়া আছে, S = {(-2, 4),(-1, 1), (0,0), (1, 2), (2,4)}
S অন্বয়ের ক্রমজোড়গুলোর প্রথম উপাদানসমূহ -2, -1, 0, 1, 2 এবং দ্বিতীয় উপাদানসমূহ 4, 1, 0, 1, 4
∴ ডোমেন S= {-2, -1, 0, 1, 2} এবং রেন্জ R= {0, 1, 4} [ans]
(গ) এর সমাধানঃ দেওয়া আছে, F={(1/2.0), (1,1), (1,-1), (5/2,2), (5/2, -2)}
F অন্বয়ের ক্রমজোড়গুলোর প্রথম উপাদানসমূহ 1/2, 1, 1, 5/2, 5/2 এবং দ্বিতীয় উপাদানসমূহ 0, 1, -1, 2, -2
∴ ডোমেন F = {1/2, 1, 5/2} এবং রেন্জ R= { 0, 1, -1, 2, -2} [ans]
১৮, নিচের অন্বয়গুলোকে তালিকা পন্ধতিতে প্রকাশ কর এবং ডোমেন ও রেঞ্জ নির্ণয় কর।
ক) R = {(x,y) : x∈A, y∈A এবং x+y=1} যেখানে A = {-2, -1, 0, 1, 2}
খ) F = {(x,y) : x∈C, y∈C এবং y = 2x} যেখানে C = {-1, 0, 1, 2, 3}
(ক) এর সমাধানঃ দেওয়া আছে, A = {-2, -1, 0, 1, 2}
এবং R = {(x,y) : x∈A, y∈A এবং x+y=1}
R এর বর্ণিত শর্ত থেকে পাই, x+y=1
∴ y = 1-x
এখন x∈A এর বিভিন্ন মানের জন্য y এর বিভিন্ন মান নির্ণয় করি:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
3 |
2 |
1 |
0 |
-1 |
কিন্তু 3 ∉ A
(খ) এর সমাধানঃ দেওয়া আছে, C = {-1, 0, 1, 2, 3}
এবং F = {(x,y) : x∈C, y∈C এবং y = 2x}
F এর বর্ণিত শর্ত থেকে পাই, y = 2x
এখন x∈C এর বিভিন্ন মানের জন্য y এর বিভিন্ন মান নির্ণয় করি:
|
x |
-1 |
0 |
1 |
2 |
3 |
|
y |
-2 |
0 |
2 |
4 |
6 |
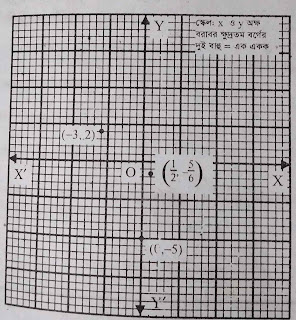
১৯। ছক কাগজে (-3,2),(0, -5), (1/2, -5/6) বিন্দুগুলো স্থাপন কর।
সমাধানঃ ছক কাগজে উভয় অক্ষ বরাবর ক্ষুদ্রতম ২ বর্গঘর সমান একক ধরে (-3,2) , (0,-5), (1/2, -5/6) বিন্দুগুলো ছক কাগজে স্থাপন করা হলো।
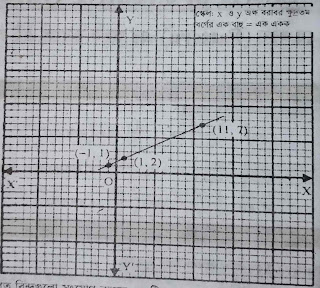
২০। ছক কাগজে (1,2), (-1)1), (11,7) বিন্দু তিনটি স্থাপন করে দেখাও যে, বিন্দু তিনটি একই সরলরেখায় অবস্থিত।
সমাধানঃ ছক কাগজে উভয় অক্ষ বরাবর ক্ষুদ্রতম ১ বর্গঘর সমান একক ধরে (-3,2) , (0,-5), (1/2, -5/6) বিন্দুগুলো ছক কাগজে স্থাপন করা হলো।
স্থাপিত বিন্দুুগুলো সংযোগ করলে একটি সরলরেখা পাওয়া যায়।
সুতরাং বিন্দু তিনটি একই সরলরেখায় অবস্থিত (দেখানো হলো)
২১। সার্বিক সেট U= {x: x ∈ N এবং x বিজোড় সংখ্যা }
A = {x: x ∈ N এবং 2 ≤ x ≤ 7}
B = {x: x ∈ N এবং 3 <x < 6}
C = {x: x ∈ N এবং x² >5 এবং x³ < 130}
ক) A সেটকে তালিকা পদ্ধতিতে প্রকাশ কর।
খ) A’ এবং CB নির্ণয় কর।
গ) B×C এবং P(A∩C) নির্ণয় কর।
(ক) এর সমাধানঃ U= {x: x ∈ N এবং x বিজোড় সংখ্যা }
U = {1, 3, 5, 7, 9, . . . . }
A = A = {x: x ∈ N এবং 2 ≤ x ≤ 7}
∴ A = {3,5,7} [ans]
(খ) এর সমাধানঃ U = {1, 3, 5, 7, 9, . . . . }
‘ক’ হতে পাই, A = {3,5,7}
∴ A’ = U-A
= {1, 3, 5, 7, 9, . . . . } – {3,5,7}
= {1,9, 11, 13, . . . .}
আবার, C = {x: x ∈ N এবং x² >5 এবং x³ < 130}
এখানে সার্বিক সেট U বিজোড় স্বাভাবিক সংখ্যার সেট। A, B, C প্রত্যেকেই U এর উপসেট তাই সকলেই হবে বিজোড় স্বাভাবিক সংখ্যা। C বিজোড় সংখ্যা হবে এবং এর বর্গ ৫ থেকে বড় এবং এর ঘন ১৩০ থেকে ছোট হবে।
বিজোড় স্বাভাবিক সংখ্যার সেট {1, 3, 5, 7, 9, . . . . }
x = 1 হলে, x²= 1² = 1 ≯ 5 এবং x³ = 1³ = 1 < 130 যা গ্রহনযোগ্য নয়।
x = 3 হলে, x²= 3² = 9 >5 এবং x³ = 3³ = 27 < 130 যা গ্রহনযোগ্য।
x = 5 হলে, x²= 5² = 25 >5 এবং x³ = 5³ = 125 < 130 যা গ্রহনযোগ্য।
x = 7 হলে, x²= 7² = 49 >5 এবং x³ = 7³ = 343 ⊀ 130 যা গ্রহনযোগ্য।
x এর মান 3,5 হলে প্রদত্ত শর্ত দুইটি গ্রহনযোগ্য।
∴ C = {3,5}
আবার, B = {x: x ∈ N এবং 3 <x < 6}
= {5}
∴ C B = {3,5} {5}
= {3} [ans]
(গ) এর সমাধানঃ
এখানে, A = {3,5,7}
B = {5}
C = {3,5}
∴ C × B = {3,5}×{5}
= {(3,5), (5,5)}
আবার, A⋂C = {3,5,7} ⋂ {3,5}
={3,5}
∴P(A⋂C) = {{3,5}, {3}, {5} ∅} [ans]
২২। ভেনচিত্রটি লক্ষ করি:
ক) B সেটকে সেট গঠন পদ্ধতিতে প্রকাশ কর।
খ) উদ্দীপক ব্যবহার করে A∪(B∩C) = (A∪B)∩(A∪C) সম্পর্কটির সত্যতা যাচাই কর।
গ) S=(B∪C)’ ×A হলে, ডোম S নির্ণয় কর।
(ক)-এর সমাধানঃ B সেটের প্রতোকটি উপাদান স্বাভাবিক সংখ্যার অন্তর্ভূক্ত একই সাথে
মৌলিক সংখ্যাও। যারা 2 এর চেয়ে ছোট নয় এবং 7 এর চেয়ে বড় নয়।
ভেনচিত্র হতে, B= {2, 3,5,7}
∴ সেট গঠন পদ্ধতিতে B = {x ∈ N: x মৌলিক সংখ্যা এবং 2 ≤ x ≤ 7 }
(খ)এর সমাধানঃ ’ক’ হতে পাই B= {2, 3,5,7}
ভেনচিত্র থেকে, A= {1, 2, 3,4}
C= {3, 4, 5, 6}
ata. B∩C = {2, 3,5,7} ∩ {3, 4, 5, 6}
= {3,5}
∴ A∪(B∩C) = {1, 2, 3,4}∪ {3,5}
= {1,2,3,4,5} – – – -(i)
আবার, A∪B = {1, 2, 3,4}∪{2, 3,5,7}
= {1,2,3,4,5,7}
A∪C = {1, 2, 3,4}∪{3, 4, 5, 6}
= {1,2,3,4,5,6}
∴ (A∪B)∩(A∪C) = {1,2,3,4,5,7}∩{1,2,3,4,5,6}
= {1,2,3,4,5} – – – – – (ii)
সুতরাং (i) ও (ii) নং তুলনা করে পাই,
A∪(B∩C) = (A∪B)∩(A∪C) [সম্পর্কটির সত্যতা যাচাই কর হলো]
(গ) এর সমাধানঃ ’ক’ হতে পাই B= {2, 3,5,7}
C= {3, 4, 5, 6}
ভেনচিত্র থেকে, A= {1, 2, 3,4}
ভেনচিত্র হতে, U = {1,2,3,4,5,6,7,8}
এখন B∪C = {2, 3,5,7} ∪ {3, 4, 5, 6}
= {2,3,4,5,6,7}
( B∪C)’ = U – ( B∪C)
= {1,2,3,4,5,6,7,8} – {2,3,4,5,6,7}
= {1,8}
∴ S = ( B∪C)’ × A
= {1,8}× {1, 2, 3,4}
= {(1,1), (1,2), (1,3), (1,4), (8,1), (8,2), (8,3), (8,4)
কোনো অন্বয়ের ক্রমজোড়গুলোর প্রথম উপাদানগুলোর সেটকে ডোমেন বলা হয়।
∴ ডোম S = {1,8} [ans]
বাছাই করা সেরা Good Night SMS In Bangla
![এসএসসি সাধারণ গণিত অনুশীলনী ২.২ সেট ফাংশন প্রশ্ন সমাধান [ ssc math chapter 2.2 set and function question & answer ] এসএসসি সাধারণ গণিত অনুশীলনী ২.২ সেট ফাংশন প্রশ্ন সমাধান [ ssc math chapter 2.2 set and function question & answer ]](https://1.bp.blogspot.com/-EDUkyunr5o4/X-ay8Vpa6LI/AAAAAAAABek/klz3RcXa5cU_xTaG2nbKHAlJ7LPzJ0yyACLcBGAsYHQ/w640-h360/%25E0%25A6%258F%25E0%25A6%25B8%25E0%25A6%258F%25E0%25A6%25B8%25E0%25A6%25B8%25E0%25A6%25BF%2B%25E0%25A6%2597%25E0%25A6%25A3%25E0%25A6%25BF%25E0%25A6%25A4%2B%25E0%25A6%2585%25E0%25A6%25A8%25E0%25A7%2581%25E0%25A6%25B6%25E0%25A7%2580%25E0%25A6%25B2%25E0%25A6%25A8%25E0%25A7%2580%2B%25E0%25A7%25A8.%25E0%25A7%25A8%2B%25E0%25A6%25B8%25E0%25A7%2587%25E0%25A6%259F%2B%25E0%25A6%2593%2B%25E0%25A6%25AB%25E0%25A6%25BE%25E0%25A6%2582%25E0%25A6%25B6%25E0%25A6%25A8%2B%25E0%25A6%25AA%25E0%25A7%258D%25E0%25A6%25B0%25E0%25A6%25B6%25E0%25A7%258D%25E0%25A6%25A8%2B%25E0%25A6%25B8%25E0%25A6%25AE%25E0%25A6%25BE%25E0%25A6%25A7%25E0%25A6%25BE%25E0%25A6%25A8.jpg)