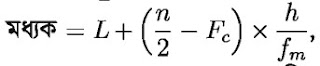উপাত্ত কাকে বলে?
উপাত্তঃ কোনাে তথ্য বা ঘটনা নির্দেশক সংখ্যাসমূহকে পরিসংখ্যানের। উপাত্ত বলে।
উদাহরণ: 50 নম্বরের মধ্যে 5 জন প্রার্থীর প্রাপ্ত নম্বর 20, 35, 45, 40, 30। এটি একটি পরিসংখ্যান এবং নম্বরগুলাে । পরিসংখ্যানের উপাত্ত ।
পরিসংখ্যান কি বা কাকে বলে?
পরিসংখ্যানঃ বিজ্ঞানভিত্তিক কৌশল যার দ্বারা সংখ্যাসূচক তথ্য বা উপাত্ত সংগ্রহ, উপাত্তের উপস্থাপন, উপাত্তের বিশ্লেষণ এবং উপাত্তসমূহ হতে প্রয়ােজনীয় সিদ্ধান্ত গ্রহণ সম্ভব হয় তাকে পরিসংখ্যান বলে।
পরিসংখ্যানের কাঁচামাল কি?
পরিসংখ্যানের কাঁচামালঃ গুণবাচক নয় এমন সংখ্যাসূচক তথ্যাবলি পরিসংখ্যানের উপাত্ত। অনুসন্ধানাধীন উপাত্তই পরিসংখ্যানের কাঁচামাল।
পরিসংখ্যান এর বৈশিষ্ট্য গুলো কি কি?
পরিসংখ্যানের বৈশিষ্ট্যঃ পরিসংখ্যানের কতকগুলাে মৌলিক বৈশিষ্ট্য হলােঃ
১। পরিসংখ্যান উপাত্তের সমষ্টি।
২। পরিসংখ্যান নির্দিষ্ট উদ্দেশ্য সম্পর্কিত।
৩। পরিসংখ্যান তুলনাযােগ্য ও বিভিন্ন গ্রুপে বিন্যাসযােগ্য তথ্য।
পরিসংখ্যান সংখ্যায় প্রকাশিত তথ্যঃ পরিসংখ্যানের উপাত্তসমূহ সংখ্যায় প্রকাশ করতে হয়। গুণবাচক তথ্য পরিসংখ্যান নয়।
বিন্যস্ত উপাত্ত কাকে বলে?
বিন্যস্ত উপাত্তঃ যেসব উপাত্ত মানের উর্ধ্বক্রম বা অধক্রম অনুসারে সাজানাে থাকে তাকে বিন্যস্ত উপাত্ত বলে।। উদাহরণ: 1 থেকে 5 পর্যন্ত সংখ্যাগুলাে ক্রমান্বয়ে লিখে পাই: 1, 2, 3, 4, 5। এই
উপাত্তগুলাে বিন্যস্ত।
অবিন্যস্ত উপাত্ত কাকে বলে?
অবিন্যস্ত উপাত্তঃ কোনাে উপাত্তের নম্বরগুলাে যদি মানের কোন ক্রমে সাজানাে না থাকে তাহলে তাকে অবিন্যস্ত উপাত্ত বলে। উদাহরণ: 1 থেকে 5 পর্যন্ত সংখ্যাগুলাে এলােমেলােভাবে লিখে পাই: 5, 3, 2, 4,
1। এই উপাত্তগুলাে অবিন্যস্ত।
শ্রেণীবিন্যাস্ত উপাত্ত কাকে বলে?
শ্রেণিবিন্যস্ত উপাত্তঃ প্রদত্ত উপাত্তগুলােকে নির্দিষ্ট ব্যবধানে উর্ধক্রমে শ্রেণিভুক্ত করে গণসংখ্যা সারণিতে উপস্থাপন করলে ঐ উপাত্তগুলােকে শ্রেণিবিন্যস্ত উপাত্ত বলা হয়।
যেমন : একটি স্কুলের ১০ম শ্রেণির ৫০ জন ছাত্রের গণিতে প্রাপ্ত নম্বরের শ্রেণিবিন্যস্ত উপাত্ত নিম্নরূপঃ
পরিসংখ্যানে চলক কি?
চলকঃ আমরা জানি, সংখ্যাসূচক তথ্যসমূহ পরিসংখ্যানের উপাত্ত। উপাত্তে ব্যবহৃত এসব সংখ্যাসমূহকে চলক বলে।
বিন্যস্ত চলক কি?
বিচ্ছিন্ন চলকঃ যে সকল চলকের মান শুধুমাত্র পূর্ণসংখ্যা হয় সেগুলােকে বিচ্ছিন্ন চলক বলে। যেমন: জনসংখ্যামূলক উপত্তর চলক।
অবিন্যস্ত চলক কি?
অবিচ্ছিন্ন চলকঃ যে সকল চলকের মান যেকোন বাস্তব সংখ্যা হতে পারে সে সকল চলককে অবিচ্ছিন্ন চলক বলে। যেমন: বয়স, উচ্চতা, ওজন সংশ্লিষ্ট উপাত্ত ।
ট্যালি চিহ্ন কাকে বলে?
ট্যালি চিহ্নঃ ট্যালি চিহ্ন হল এক ধরনের ইউনারি সংখ্যাগত পদ্ধতি। এটি মূলত হিসাব বা গণনার জন্য ব্যবহৃত সংখ্যাবাচক চিহ্ন।
গণসংখ্যা নিবেশন সারণি নির্ণয়
গণসংখ্যা নিবেশন সারণি (Frequency Distribution Table): কোনাে পরিসংখ্যানের উপাত্তগুলােকে উপস্থিতি। সংখ্যা (Frequency)’র ভিত্তিতে শ্রেণিব্যবধান ও শ্রেণিসংখ্যা নির্ণয়ের মাধ্যমে একটি ছক আকারে বিন্যস্ত করলে তাকে গণসংখ্যা নিবেশন সারণি বলা হয়।
গণসংখ্যা নিবেশন সারণি তৈরির ধাপসমূহ:
১. পরিসর নির্ণয় ।
২. শ্রেণিব্যাপ্তি নির্ণয়।
৩. শ্রেণিসংখ্যা নির্ণয়।
৪. ট্যালি চিহ্নের সাহায্যে গণসংখ্যা নির্ণয়
৫. ক্রমযোজিত গণসংখ্যা নির্ণয়
পরিসর নির্ণয়ঃ
পরিসর = (সর্বোচ্চ মান – সর্বনিম্ন মান) +১
শ্রেণিব্যাপ্তি নির্ণয়ঃ
বিচ্ছিন্ন শ্রেণিসীমার ক্ষেত্রেঃ
শ্রেণি ব্যবধান বা শ্রেণিব্যাপ্তি = (শ্রেনীর সর্বোচ্চ মান – শ্রেণীর সর্বনিম্ন মান)+ 1
অবিচ্ছিন্ন শ্রেণিসীমা ক্ষেত্রে ঃ
শ্রেণি ব্যবধান শ্রেণিব্যাপ্তি = শ্রেনীর সর্বোচ্চ মান – শ্রেণীর সর্বনিম্ন মান
শ্রেণিসংখ্যা নির্ণয়ঃ
পরিসর
শ্রেণিসংখ্যা = —————–
শ্রেণিব্যাপ্তি
ট্যালি নির্ণয়ঃ প্রথমে অবিন্যস্ত উপাত্ত থাকলে সেগুলোকে বিন্যস্ত করে নিতে হয় এরপর একটি করে সংখ্যা আঙ্গুল দিয়ে ধরে সেই সংখ্যাটি কোন শ্রেণীতে পড়ছে সেই শ্রেণি সোজাসোজি ট্যালি ঘরে একটি দাগ দিতে হবে এভাবে চারটি দাগ হলে পরবর্তী দাগটি দিয়ে কেটে দিতে হবে।
ক্রমযোজিত গণসংখ্যা (Cumulative Frequency): কোনাে শ্রেণির এবং তার সকল পূর্ববর্তী শ্রেণির গণসংখ্যার সমষ্টিকে ঐ শ্রেণির ক্রমযােজিত গণসংখ্যা বলা হয়।
যেমন কোনাে গণসংখ্যা নিবেশনের প্রথম তিনটি শ্রেণির গণসংখ্যা যথাক্রমে 7, 10 ও 12 হলে-
প্রথম শ্রেণির ক্রমযােজিত গণসংখ্যা = 7
দ্বিতীয় শ্রেণির ক্রমযােজিত গণসংখ্যা = 7+ 10 = 17
তৃতীয় শ্রেণির ক্রমযােজিত গণসংখ্যা = 7.+ 10 + 12 = 29
আয়তলেখ অঙ্কন
আয়তলেখ, বহুভুজ, অজিভ রেখা অঙ্কন করতে যা যা করতে হবেঃ
- আয়তলেখ অঙ্কন করতে অবিচ্ছিন্ন শ্রেণিব্যপ্তি লাগবে।
- বহুভুজ আকতে শ্রেণি মধ্যমান লাগবে।
- অজিভ রেখা আঁকতে ক্রমযোজিত গণসংখ্যা লাগবে।
প্রকৃত উচ্চসীমা এবং প্রকৃত নিম্নসীমাঃ কোনাে বিচ্ছিন্ন শ্রেণির উচ্চসীমা এবং পরবর্তী শ্রেণির নিম্নসীমার মধ্যবিন্দুকে সেই শ্রেণির প্রকৃত উচ্চসীমা বলে। কোনাে শ্রেণির প্রকৃত উচ্চসীমা পরবর্তী শ্রেণির প্রকৃত নিম্নসীমা হবে । উদাহরণ ঃ
প্রথম শ্রেণীর প্রকৃত নিম্নসীমা 39.5 এবং উচ্চসীমা 44.5। দ্বিতীয় শ্রেণীর নিম্নসীমা 44.5 এবং উচ্চসীমা 49.5
বিচ্ছিন্ন শ্রেণি ব্যবধানঃ (Discontinuous Class Interval) কোন শ্রেণির উধ্বসীমার পরবর্তী সংখ্যা যদি পরবর্তী শ্রেণির নিষ্কাশীনা হয় এবং এভাবে ক্রমান্বয়ে শ্রেণিসীরা তৈরি করা হয়। তবে তাকে বিচ্ছিন্ন শ্রেণিসীমা বলা হয়। যেমন: 45-49, 50-54, 55-59 ইত্যাদি ।
অবিচ্ছিন্ন শ্রেণি ব্যবধানঃ (Continuous Class Interval) যদি কোন শ্রেণির উর্ধসীমা পরবর্তী শ্রেণির নিম্নসীমা হয় এবং ঐ শ্রেণির উর্ধ্বসীমা তার পরবর্তী শ্রেণির নিসীমা হয় এবং এভাবে ক্রমান্বয়ে চলতে থাকে তবে সেই অবিচ্ছিন্ন চলকসমূহকে নিয়ে গঠিত শ্রেণিসীমাকে অবিচ্ছিন্ন শ্রেণিসীমা বলা
হয়। যেমন: উপরের সারণি থেকে 44.5-49.5, 49.5-54.5, 54.5-59.5 ‘ইত্যাদি।
বিচ্ছিন্ন শ্রেণি ব্যবধানকে অবিচ্ছিন্ন করার পদ্ধতিঃ
সহজ পদ্ধতিঃ নিম্নসীমা থেকে ০.৫ কমাবে এবং উচ্চসীমা থেকে ০.৫ বাড়াবে। নিচের ছবিটি ভালো করে লক্ষ কর।
আসল পদ্ধতিঃ
শ্রেণির নিম্নসীমা = আলােচ্য শ্রেণির নিম্নসীমা – {(আলােচ্য শ্রেণির নিম্নসীমা – পূর্ববর্তী শ্রেণির উর্ধ্বসীমা) ÷ 2}
শ্রেণির উর্ধ্বসীমা = আলােচ্য শ্রেণির উর্ধ্বসীমা + {(পরবর্তি শ্রেণির নিম্নসীমা – আলোচ্য শ্রেণির উর্ধ্বসীমা) ÷ 2}
গণসংখ্যা বহুভুজ অঙ্কন
গণসংখ্যা বহুভুজ (Frequency Polygon): অবিচ্ছিন্ন উপাত্তের শ্রেণি ব্যবধানের বিপরীত গণসংখ্যা নির্দেশক বিন্দুসমূহকে পর্যায়ক্রমে রেখাংশ দ্বারা যুক্ত করে যে লেখচিত্র পাওয়া যায় তাই হলাে গণসংখ্যা
বহুভুজ। গণসংখ্যা বহুভুজ দুই ভাবে অঙ্কন করা যায়। যথা :
- আয়তলেখ ব্যবহার করে গণসংখ্যা বহুভুজ অঙ্কন
- আয়তলেখ ব্যবহার না করে গণসংখ্যা বহুভুজ অঙ্কন
নিম্নে পদ্ধতি দুইটি সম্পর্কে আলােচনা করা হল
১। ‘আয়তলেখ ব্যবহার করে গণসংখ্যা বহুভুজ অঙ্কনঃ
- আয়তলেখের আয়তসমূহের ভূমির সমান্তরাল বিপরীত বাহুর মধ্যবিন্দুসমূহ নির্ধারণ করতে হবে।
- চিহ্নিত মধ্যবিন্দুসমূহ রেখাংশ দ্বারা সংযুক্ত করলেই গণসংখ্যা বহুভূজ পাওয়া যাবে। তবে গণসংখ্যা বহুভুজ সুন্দর দেখানাের জন্য প্রথম ও শেষ আয়তের মধ্যবিন্দুর সংযােগ রেখাংশের প্রান্ত বিন্দুদ্বয়। শ্রেণি ব্যবধান নির্দেশক x-অক্ষের সাথে সংযুক্ত করা যেতে পারে।
২। আয়তলেখ ব্যবহার না করে গণসংখ্যা বহুভুজ অঙ্কনঃ
- বিচ্ছিন্ন শ্রেণি ব্যবধানের মধ্যবিন্দু বের করতে হবে।
- x-অক্ষ বরাবর শ্রেণি ব্যবধান এবং y-অক্ষ বরাবর গণসংখ্যা স্থাপন করতে হবে। শ্রেণি ব্যবধানের মধ্যবিন্দুর বিপরীতে গণসংখ্যাগুলাে বসিয়ে প্রাপ্ত বিন্দুসমূহ রেখাংশ দ্বারা সংযুক্ত করলে গণসংখ্যা বহুভুজ পাওয়া যাবে।
Note: আয়তলেখ ব্যবহার করে গণসংখ্যা বহুভুজ অঙ্কনের ক্ষেত্রে বিচ্ছিন্ন শ্রেণি ব্যবধানকে অবশ্যই অবিচ্ছিন্ন শ্রেণি ব্যবধানে রূপান্তর করতে হবে। কিন্তু আয়তলেখ ব্যবহার না করে গণসংখ্যা বহুভুজ অঙ্কনের ক্ষেত্রে বিচ্ছিন্ন শ্রেণি ব্যবধানকে অবিচ্ছিন্ন শ্রেণি ব্যবধানে রূপান্তর না করাই শ্রেয়।
ক্রমযােজিত গণসংখ্যা লেখাঙ্কন বা অজিভ রেখা অঙ্কন
ক্রমযােজিত গণসংখ্যা লেখাঙ্কন বা অজিভ রেখা (0give Curve): কোনাে উপাওের শ্রেণিকরণের পর শ্রেণি ব্যাপ্তির উচ্চসীমা x অক্ষ বরাবর এবং শ্রেণির ক্রমযােজিত গণসংখ্যা y অক্ষ বরাবর স্থাপন করে ক্রমযােজিত গণসংখ্যার লেখা বা অজিভ রেখা পাওয়া যায় ।
কেন্দ্রীয় প্রবণত (Central Tendency): অবিন্যস্ত উপাত্তসমূহ। মানের এমানুসারে সাজালে, উপাত্তসমূহ মাঝামাঝি কোনো মানের। কাছাকাছি পুঞ্জিভূত হয়। আবার গণসংখ্যা নিবেশন সারণিতে উপস্থাপন। করা হলে মাঝামাঝি কোনো একটি শ্রেণিতে গণসংখ্যার প্রাচুর্য দেখা যায়। উপাত্তসমূহের মাঝামাঝি মানের দিকে বা মাঝামাঝি শ্রেণির দিকে পুঞ্জিভূত হওয়ার এই প্রবণতাকে কেন্দ্রীয় প্রবণতা বলে।
সাধারণভাবে কেন্দ্রিয় প্রবণতার পরিমাপ হল:
(ক) মধ্যক; (খ) গাণিতিক গড় বা গড়; (গ) প্রচুরক ।
মধ্যক নির্ণয়
মধ্যক কিভাবে নির্ণয় করতে হবে তা প্রদত্ত উপাত্তের উপরে নির্ভর করে। যেমনঃ
নিয়ম-১ঃ বিন্যস্ত অবিন্যস্ত উপাত্তের মধ্যক নির্ণয়
১০, ২০, ৩৫, ৪২, ১৪, ২৪, ২২, ২৬, ৪০, ৩০ এভাবে থাকলে
প্রথমে উপাত্ত সমূহকে বিন্যস্ত করে নিতে হবে।
উপাত্তের মোট সংখ্যা বিজোড় হলে মধ্যক হবে = (n+1)÷2 তম পদ
উপাত্তের মোট সংখ্যা জোড় হলে মধ্যক হবে = {n÷2 তম পদ+(n+1)÷2 তম পদ}÷2
নিয়ম-২ঃ শ্রেণিবিন্যস্ত উপাত্তের মধ্যক নির্ণয়
|
উচ্চতা (সেমি) |
150 |
155 |
160 |
165 |
170 |
175 |
|
গণসংখ্যা |
4 |
6 |
12 |
16 |
8 |
5 |
উপাত্ত উপরের মত দেওয়া থাকলে ক্রমযোজিত গণসংখ্যা বের করে আগের মত করে মধ্যক বের করতে হবে।
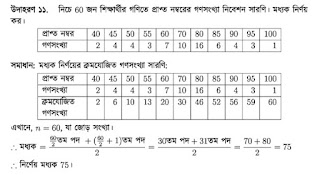
নিয়ম-৩ঃ শ্রেণিবিন্যস্ত উপাত্তের মধ্যক নির্ণয়
|
সেকেন্ড |
30-35 |
36-41 |
42-47 |
48-53 |
54-59 |
60-65 |
|
গণসংখ্যা |
4 |
6 |
12 |
16 |
8 |
5 |
উপাত্ত উপরের মত দেওয়া থাকলে নিচের সূত্র দিয়ে মধ্যক বের করতে হবে।
যেখানে ,
L = হলো যে শ্রেণিতে মধ্যক অবস্থিত সেই শ্রেণির নিন্নসীমা,
n = গণসংখ্যা,
Fc = মধ্যক শ্রেণির পূর্ববর্তী শ্রেণির যোজিত গণসংখ্যা,
fm = মধ্যক শ্রেণির গণসংখ্যা
h = শ্রেণি ব্যাপ্তি
উদাহরণঃ
গড় নির্ণয়
গাণিতিক গড় (Arithmetic Mean): সংগৃহীত উপাত্তসমূহের চলকের মানের সমষ্টিকে যদি চলকের সংখ্যা দ্বারা ভাগ করা হয়, তবে গাণিতিক গড় পাওয়া যায়।
গড় চার ভাবে নির্ণয় করা লাগতে পারে। যথাঃ
- সাধারণ গড় নির্ণয়
- সারণি থেকে গড় নির্ণয়
- সারণি থেকে সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয়।
- গুরুত্বযুক্ত উপাত্তের গড় নির্ণয়।
প্রচুরক নির্ণয়
প্রচুরক (Mode): কোন উপাত্তে যে সংখ্যা সর্বাধিক বার উপস্থাপিত হয়, সেই সংখ্যাই উপাত্তের প্রচুরক। একটি উপাত্তের এক বা একাধিক প্রচুরক থাকতে পারে। কোন উপাত্তে যদি কোন সংখ্যাই একাধিকবার । থাকে তবে সেই উপাত্তের কোন প্রচুরক নেই।
একটি সমস্যা থেকে সকল প্রশ্নের সমাধান করো
কোনো স্কুলে নবম শ্রেণির বার্ষিক পরীক্ষার 50 জন শিক্ষার্থীর গণিতে প্রাপ্ত নম্বর নিম্নরূপ :
75, 68, 60, 76, 68, 64, 58, 70, 45, 49, 60, 50, 48, 51, 78, 58, 55, 58, 75, 61, 62, 44, 64, 63, 70, 70, 67, 71. 55, 54, 61, 63, 60, 69, 70, 69, 70, 67, 56, 62, 60, 63, 56, 57, 50, 60, 56, 61, 63, 65
- উপাত্তগুলো বিন্যস্ত করো
- মধ্যক নির্ণয় করো
- প্রচুরক নির্ণয় করো
- সাধারণ পদ্ধতিতে গড় নির্ণয় করো
- পরিসর নির্ণয় করো
- গণসংখ্যা নিবেশন সারণি তৈরি করো
- ক্রমযোজিত গণসংখ্যা নির্ণয় করো
- আয়তলেখ, বহুভুজ, অজিভ রেখা অংকন করো
- সারণি থেকে গড় নির্ণয় করো
- সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয় কর
- সারণি থেকে মধ্যক নির্ণয় করো
- প্রচুরক নির্ণয় করো