প্রিয় শিক্ষার্থী বন্ধুরা আজকে আমরা নবম শ্রেণির গণিত অ্যাসাইনমেন্ট সমাধান ১ম সপ্তাহ ২০২২ দেখবো। এই প্রথম সপ্তাহ গণিত নবম শ্রেণী অ্যাসাইনমেন্টটি তোমাদের সাধারণ গণিত দ্বিতীয় অধ্যায় সেট ফাংশন থেকে দেওয়া হয়েছে।
নবম শ্রেণির ১ম সপ্তাহ গণিত অ্যাসাইনমেন্ট ২০২২
গণিত ২০২২ অ্যাসাইনমেন্ট নবম শ্রেণী লেখার আগে তোমাদের আজকের এই পোস্টটি সম্পুর্ণ পড়া উচিত। নবম শ্রেণির গণিত অ্যাসাইনমেন্ট সমাধান ১ম সপ্তাহ ২০২২ পোস্টটি সম্পুর্ণ পড়লে তোমরা এটি কিভাবে লিখতে হবে তার একটি পূর্ণাঙ্গ গাইডলাইন পেয়ে যাবে।
করোনাকালীন সময়ে মাধ্যমিক ও উচ্চশিক্ষা অধিদপ্তর অ্যাসাইনমেন্ট ২০২২ প্রকাশ করেছে। এই মুহূর্তে ষষ্ঠ থেকে দশম শ্রেণী, এসএসসি ২০২২ ব্যাচ, ও এইচএসসি ২০২২ এর জন্য অ্যাসাইনমেন্ট চলছে। তারমধ্যে ষষ্ঠ থেকে দশম শ্রেণীর শিক্ষার্থীদের জন্য প্রথম সপ্তাহের এসাইনমেন্ট দেয়া হয়েছে।
১ম সপ্তাহ অ্যাসাইনমেন্ট ২০২২ গণিত নবম শ্রেণী তোমাদের দুটি অ্যাসাইনমেন্ট এর একটি। প্রথম সপ্তাহে নবম শ্রেণীর জন্য দুইটি অ্যাসাইনমেন্ট লিখতে হবে যার অন্যটি হলো বাংলা। তোমরা আজকের পোষ্টে বাংলা এসাইনমেন্ট ২০২২ এর সমাধান লিঙ্ক পেয়ে যাবে সেখান থেকে তোমরা সেটি লিখে নিতে পারবে।
৯ম শ্রেণির গণিত ১ম সপ্তাহ সমাধান অ্যাসাইনমেন্ট ২০২২
গণিত অ্যাসাইনমেন্ট প্রথম সপ্তাহ ২০২২ উত্তর লেখার আগে তোমরা প্রশ্নগুলো অবশ্যই ভালোভাবে পড়ে নেবে। প্রশ্ন না পড়ে উত্তর লিখলে সেক্ষেত্রে তোমাদের অনেক ভুল-ত্রুটি থেকে যেতে পারে। তাই তোমাদের কাছে সাজেশন থাকবে তোমরা সম্পূর্ণ প্রশ্নটিই অর্থাৎ প্রশ্নের প্রত্যেকটি অংশ ভালোভাবে পড়ে তারপর নমুনা উত্তরটি সম্পূর্ণ টি দেখে নিজেরা উত্তর লেখা শুরু করবে।
উপরের প্রশ্ন গুলি পড়ে তোমরা নিশ্চয়ই বুঝতে পেরেছো গণিত অ্যাসাইনমেন্ট 2022 প্রথম সপ্তাহে তোমাদের কি উত্তর দিতে হবে এবং কিভাবে উত্তর দিতে হবে। গণিত অ্যাসাইনমেন্ট প্রশ্নে বিষয়বস্তু ও নির্দেশনা অংশে খুব সুন্দর করে বুঝিয়ে দেওয়া আছে তোমাদের উত্তর কিভাবে লিখতে হবে সেইসাথে বইয়ের রেফারেন্স দেওয়া আছে সেখান থেকে উদাহরণ দেখে উত্তরগুলো লিখতে পারো।
নবম গণিত অ্যাসাইনমেন্ট নম্বর ১
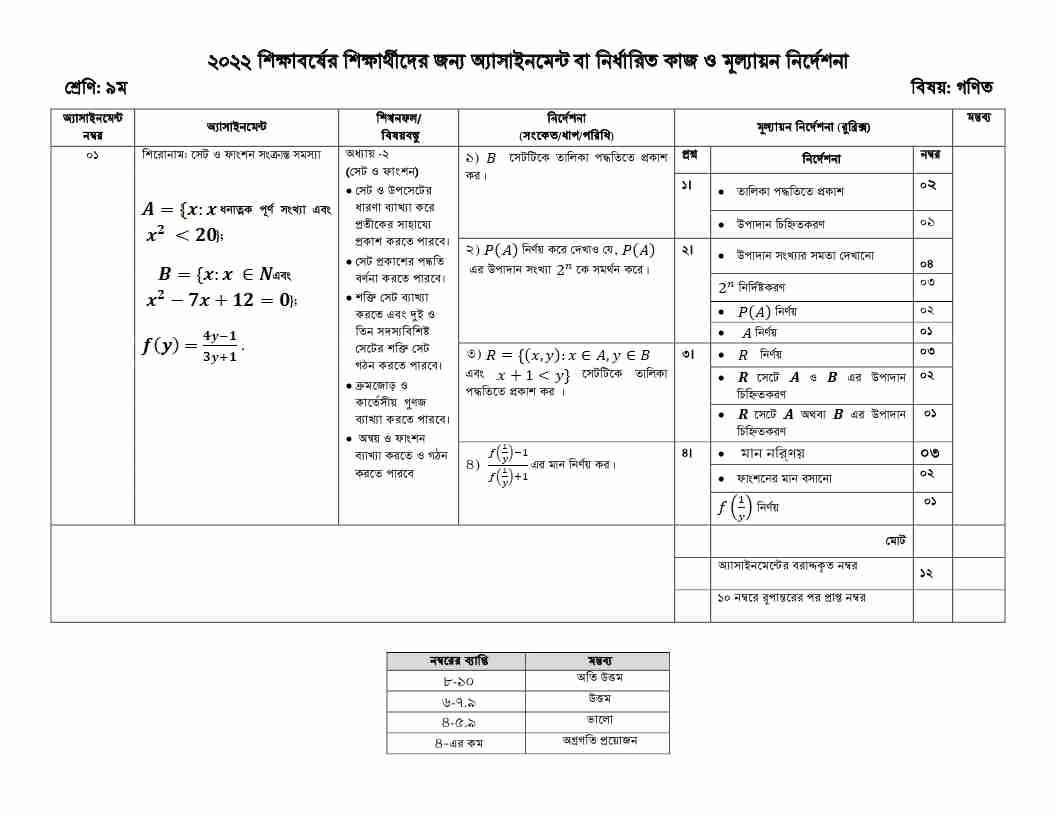
৯ম শ্রেণির গণিত অ্যাসাইনমেন্ট (শিরোনাম): সেট ও ফাংশন সংক্রান্ত সমস্যা।
A = {x:x ধনাত্মক পূর্ণ সংখ্যা এবং x2<20};
B = {x:x∈N এবং x2-7x+12 = 0};
শিখনফল/বিষয়বস্তুঃ অধ্যায়-২ (সেট ও ফাংশন)
- সেট ও উপসেটের ধারণা ব্যাখ্যা করে প্রতীকের সাহায্যে প্রকাশ করতে পারবে।
- সেট প্রকাশের পদ্ধতি বর্ণনা করতে পারবে।
- শক্তি সেট ব্যাখ্যা করতে এবং দুই তিন সদস্যবিশিষ্ট সেটের শক্তি সেট গঠন করতে পারবে।
- ক্রমজোড় ও কার্তেসীয় গুণজ ব্যাখ্যা করতে পারবে।
- অন্বয় ও ফাংশ নব্যাখ্যা করতে ও গঠন করতে পারবে।
অ্যাসাইনমেন্ট প্রণয়নের নির্দেশনা (ধাপ/পরিধি/সংকেত):
১. B সেটটিকে তালিকা পদ্ধতিতে প্রকাশ কর।
২) P(A) নির্ণয় করে দেখাও যে, P(A) এর উপাদান সংখ্যা 2n কে সমর্থন করে।
৩) R={(x,y):x∈A, y∈B এবং x+1<y} সেটটিকে তালিকা পদ্ধতিতে প্রকাশ কর।
৪) এর মান নির্ণয় কর।
আমরা যে নমুনা নবম শ্রেণির গণিত অ্যাসাইনমেন্ট সমাধান ১ম সপ্তাহ ২০২২ টি তোমাদের দিচ্ছি সেটি তোমরা প্রথমে ভালোভাবে পড়ে বুঝে নেবে তারপর উত্তর লেখা শুরু করবে। প্রশ্নগুলোর সমাধান কিভাবে করতে হবে তা জেনে নিয়ে তোমরা যদি নিজে নিজে সমাধান গুলো করতে পারো তাহলে সেটি অ্যাসাইনমেন্ট দেওয়ার মূল উদ্দেশ্য কে ফলপ্রসূ করবে।
নবম শ্রেণির গণিত ১ম সপ্তাহ অ্যাসাইনমেন্ট ২০২২ সমাধান
আজকের নবম শ্রেণির গণিত অ্যাসাইনমেন্ট সমাধান ১ম সপ্তাহ ২০২২ তোমাদের যদি ভালো লেগে থাকে তাহলে অবশ্যই নিচে শেয়ার বাটনে ক্লিক করে তোমাদের বন্ধুদের সাথে এটি শেয়ার করবে। আমরা তোমাদের 2021 সাল থেকে সকল অ্যাসাইনমেন্ট এর নমুনা সমাধান লিখে আসছি 2022 সালে চলমান রয়েছে।
অ্যাসাইনমেন্ট শুরু
১নং প্রশ্নের উত্তর
B সেটটিকে তালিকা পদ্ধতিতে প্রকাশঃ
দেওয়া আছে,
B = {x:x∈N এবং x2-7x+12 = 0}
এখানে, x2-7x+12 = 0
বা, x2-4x-3x+12 = 0
বা, x(x-4)-3(x-4) = 0
বা, (x-4)(x-3) = 0
হয়, x-4=0 অথবা, x-3=0
∴x=4 ∴x=3
∴ B সেটটিকে তালিকা পদ্ধতিতে প্রকাশ করে পাই B={3,4}
২নং প্রশ্নের উত্তর
দেওয়া আছে,
A = {x:x ধনাত্মক পূর্ণ সংখ্যা এবং x2<20}
x=1,2,3,4,5,6….. এর জন্য
x=1 হলে, x2=12=1<20
x=2 হলে, x2=22=4<20
x=3 হলে, x2=32=9<20
x=4 হলে, x2=42=16<20
x=5 হলে, x2=52=2520
সুতরাং A = {1,2,3,4}
এখন A এর উপসেট ={{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3}{1,2,4},{1,3,4}{2,3,4}{{1,2,3,4}Ø}
P(A) ={{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3}{1,2,4},{1,3,4}{2,3,4}{{1,2,3,4}Ø}
= 16 টি
এখানে, A এর উপাদান সংখ্যা n=4
এবং P(A) এর উপাদান সংখ্যা = 16 = 24=2n
সুতরাং কোনো সেট A এর উপাদান সংখ্যা n হলে P(A) এর উপাদান সংখ্যা 2n কে সমর্থন করে। (দেখানো হলো)
৩নং প্রশ্নের উত্তর
R={(x,y):x∈A, y∈B এবং x+1<y} সেটটিকে তালিকা পদ্ধতিতে প্রকাশ
দেওয়া আছে, R={(x,y):x∈A, y∈B এবং x+1<y}
’খ’ হতে পাই A = {1,2,3,4}
এবং ’ক’ হতে পাই B={3,4}
এখানে A×B= {1,2,3,4}×{3,4}
= {(1,3),(1,4),(2,3),(2,4),(3,3),(3,4)(4,4)}
x+1<y শর্তানুসারে,
R={(1,3),(1,4),(2,4)}
∴ R সেটটিকে তালিকা পদ্ধতিতে প্রকাশ করে পাই
R={(1,3),(1,4),(2,4)}
৪ নং প্রশ্নের উত্তর
দেওয়া আছে,
এখন,
বা,
বা,
বা,
বা,
বা,
বা,
∴ নির্ণেয় মান
অ্যাসাইনমেন্ট শেষ
অ্যাসাইনমেন্ট২০২২ এর সকল শ্রেণীর সকল বিষয়ের সমাধান পেতে তোমরা সমাধান ডটনেট সাইটের সাথে থাকবে সেই সাথে তোমরা আমাদের ফেসবুক পেজ ও গ্রুপ এ জয়েন করবে। অ্যাসাইনমেন্ট সমাধান নিয়ে আমাদের একটি ইউটিউব চ্যানেল রয়েছে চ্যানেলটির নাম হচ্ছে S IS FOR SCHOOL। তোমাদের অনুরোধ থাকবে তোমরা এই চ্যানেলটি সাবস্ক্রাইব করে পাশে থাকা বেল আইকনটি অন করে দেবে।
১ম সপ্তাহ গণিত অ্যাসাইনমেন্ট ২০২২
আরো পড়ুনঃ
- সকল অ্যাসাইনমেন্ট ২০২২ দেখুন এখানে
- ৭ম শ্রেণির গণিত ১ম সপ্তাহ অ্যাসাইনমেন্ট ২০২২
- দশম শ্রেণির গণিত ১ম সপ্তাহ অ্যাসাইনমেন্ট ২০২২
- ৬ষ্ঠ শ্রেণির গণিত ১ম সপ্তাহ অ্যাসাইনমেন্ট ২০২২
- ২০২২ সালের এসএসসি অ্যাসাইনমেন্ট ১০ম সপ্তাহ ইসলাম শিক্ষা
আমাদের ইউটিউব লিংক
https://www.youtube.com/channel/UCea_DqYt9NegZgE5A-mdIag
ফেজবুক পেজ (সমস্যা ও সমাধান)
https://web.facebook.com/shomadhan.net
assignment all class (6-9)📝📝
https://web.facebook.com/groups/287269229272391



