এসএসসি সাধারণ গণিত ১৬.১ অনুশীলনীর প্রশ্ন ও সমাধান

নবম-দশম শ্রেণির বা এসএসসি সাধারণ গণিত ১৬.১ অনুশীলনীর প্রশ্ন ও সমাধান নিচে দেওয়া হলো। আপনারা এখান সম্পূর্ণ নির্ভূল উত্তর পেয়ে যাবেন।

সাধারণ গণিত ১৬.১ অনুশীলনীর প্রশ্ন ও সমাধান

১৬.১ অনুশীলনী পরিমিতি

🟥 ত্রিভুজক্ষেত্রের ক্ষেত্রফল সম্পর্কিত সূত্রাবলী
ত্রিভুজক্ষেত্রের ক্ষেত্রফল = 1/2 × ভূমি × উচ্চতা
(1) সমকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ

সমকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ

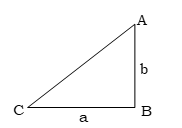
মনে করি, ABC সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় যথাক্রমে BC = a এবং AB = b। BC কে ভূমি এবং AB কে উচ্চতা বিবেচনা করলে,
ΔABC এর ক্ষেত্রফল = 1/2 × ভূমি × উচ্চতা
= 12 ab

(2) ত্রিভুজের দুই বাহু ও তাদের অন্তর্ভূক্ত কোন দেওয়া থাকলে ক্ষেত্রফল নির্ণয়ের সূত্রঃ ত্রিভুজক্ষেত্রের দুই বাহু ও তাদের অন্তর্ভুক্ত কোণ দেওয়া আছে। মনে করি, ABC ত্রিভুজের বাহুদ্বয় BC = a, CA = b, AB = c। A থেকে BC বাহুর উপর AD লম্ব আঁকি।
ধরি, উচ্চতা AD = h।
কোণ c বিবেচনা করলে পাই, ADCA = sinC
বা, h/b = sinC বা, h = b sinC

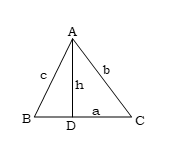
ত্রিভুজের দুই বাহু ও তাদের অন্তর্ভূক্ত কোন দেওয়া থাকলে ক্ষেত্রফল নির্ণয়ের সূত্রঃ

Δ ক্ষেত্র ABC এর ক্ষেত্রফল = 1/2 BC × AD
= 12 a × b sinC
= 12 ab sinC

অনুরূপভাবে Δ ক্ষেত্র ABC এর ক্ষেত্রফল = 12 bc sinA
= 12 ca sinB

(3) বিষমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ ত্রিভুজের তিন বাহু দেওয়া আছে। মনে করি, ΔABC এর BC = a, CA = b এবং AB = c।

বিষমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ
∴ এর পরিসীমা 2s = a + b + c
Δ ক্ষেত্র ABC এর ক্ষেত্রফল

${\rm{ = }}\sqrt {s(s - a)(s - b)(s - c)}$

(4) সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ

সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ
মনে করি, ABC সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য a
Δ ক্ষেত্র ABC এর ক্ষেত্রফল = $\frac{{\sqrt 3 }}{4}{\rm{ }}{{\rm{a}}^{\rm{2}}}$

(5) সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ

সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্রঃ
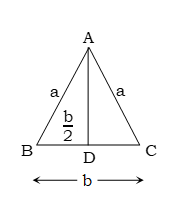
মনে করি, ABC সমদ্বিবাহু ত্রিভুজের AB = AC = a এবং BC = b
সমদ্বিবাহু Δ ক্ষেত্র ABC এর ক্ষেত্রফল = $\frac{b}{4}{\rm{ }}\sqrt {4a2 - b2}$

১৬.১ অনুশীলনীর প্রশ্ন ও সমাধান

প্রশ্ন \ 1 \ একটি সমকোণী ত্রিভুজের অতিভুজ 25 মিটার। এর একটি বাহু অপরটির 3/4 অংশ হলে, বাহু দুইটির দৈর্ঘ্য নির্ণয় কর।
সমাধান : মনে করি, ABC সমকোণী ত্রিভুজের অতিভুজ, AC = 25 মিটার, BC = x মিটার এবং AB = $\frac{{3x}}{4}$ মিটার।

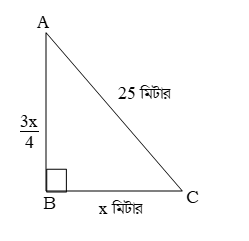
১৬.১ অনুশীলনীর প্রশ্ন ও সমাধান
পিথাগোরাসের উপপাদ্য অনুযায়ী,

$A{B^2} + {\rm{ }}B{C^2} = {\rm{ }}A{C^2}$

বা, ${\left( {\frac{{3x}}{4}} \right)^{\rm{2}}}{\rm{ + }}{{\rm{x}}^{\rm{2}}}{\rm{ = (25}}{{\rm{)}}^{\rm{2}}}$

বা, $\frac{{9{x^2}}}{{16}}{\rm{ + }}{{\rm{x}}^{\rm{2}}}{\rm{ = 625}}$

বা, $\frac{{9{x^2} + 16{x^2}}}{{16}}{\rm{ = 625}}$

বা, $25{x^2} = {\rm{ }}625 \times 16$

বা, ${{\rm{x}}^{\rm{2}}}{\rm{ = }}\frac{{625 \times 16}}{{25}} = 400$

∴ ${\rm{x = }}\sqrt {400} {\rm{ = }}\sqrt {{{(20)}^2}} {\rm{ = 20 }}$

[দৈর্ঘ্য ঋণাত্মক হতে পারে না তাই ধনাত্মক মান নেওয়া হলো]
∴ একটি বাহুর দৈর্ঘ্য = 20 মিটার
∴ অপর বাহুটির দৈর্ঘ্য = 20 × $\frac{3}{4}$ মিটার বা 15 মিটার
নির্ণেয় বাহু দুইটির দৈর্ঘ্য যথাক্রমে 20 মিটার এবং 15 মিটার।

প্রশ্ন \ 2 \ 20 মিটার লম্বা একটি মই দেওয়ালের সাথে খাড়াভাবে আছে। মইটির গোড়া দেওয়াল থেকে কত দূরে সরালে ওপরের প্রান্ত 4 মিটার নিচে নামবে?
সমাধান :
মনে করি, AC মইয়ের গোড়া c থেকে উ বিন্দুতে সরালে ওপরের প্রান্ত অ থেকে 4 মিটার নিচে B বিন্দুতে নামবে। মইয়ের দৈর্ঘ্য = AC = BD = 20 মি. এবং AB = 4 মি.
∴ BC = (20 – 4) মিটার = 16 মিটার

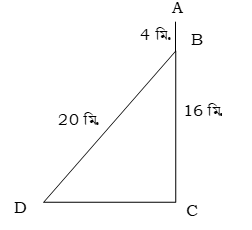
এখন, সমকোণী ত্রিভুজ BCD এ BC2 + CD2 = BD2
বা, CD2 = BD2 – BC2
= (20)2 – (16)2 = 400 – 256 = 144
∴ CD = 12
দেওয়াল থেকে মইটির গোড়ার দূরত্ব 12 মিটার। (Ans)

প্রশ্ন \ 3 \ একটি সমদ্বিবাহু ত্রিভুজের পরিসীমা 16 মিটার। এর সমান সমান বাহুর দৈর্ঘ্য ভূমির $\frac{5}{6}$ অংশ হলে, ত্রিভুজক্ষেত্রটির ক্ষেত্রফল নির্ণয় কর।
সমাধান : মনে করি, ABC একটি সমদ্বিবাহু ত্রিভুজ এবং এর

ভূমি =x মিটার
∴ AB = AC = $\frac{5}{6}$
প্রশ্নানুসারে, X + $\frac{{5x}}{6}$ + $\frac{{5x}}{6}$ = 16
বা, 16 x = 96

বা, x = 6
অতএব, BC = 6 মিটার এবং

AB = AC = $\frac{{5 \times 6}}{6}$ = 5 মিটার
ধরি, a = 6 মি., b = 5 মি., c = 5 মি.
Δ ক্ষেত্র ABC এর পরিসীমা 2s = (6 + 5 + 5) মিটার
= 16 মিটার
∴ s = 8 মিটার
∴ Δ ক্ষেত্র ABC এর ক্ষেত্রফল
= $\sqrt {s(s - a)(s - b)(s - c)}$ বর্গমিটার
= $\sqrt {8(8 - 6)(8 - 5)(8 - 5)}$ বর্গমিটার
= $\sqrt {8 \times 2 \times 3 \times 3}$ বর্গমিটার
= $\sqrt {144}$ বর্গমিটার
= 12 বর্গমিটার
ত্রিভুজক্ষেত্রটির ক্ষেত্রফল 12 বর্গমিটার। (Ans)

প্রশ্ন \ 4 \ একটি ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য 25 সে. মি., 27 সে. মি. এবং পরিসীমা 84 সে. মি.। ত্রিভুজটির ক্ষেত্রফল নির্ণয় কর।
সমাধান : মনে করি, ABC ত্রিভুজটির দুইটি বাহুর দৈর্ঘ্য BC = a = 25 সে.মি. ও AC = b = 27 সে. মি.

এবং পরিসীমা 2s = 84 সে. মি.
∴ s = $\frac{{84}}{2}$ সে. মি. = 42 সে. মি.
ধরি, ত্রিভুজটির অপর বাহুর দৈর্ঘ্য = AB = c
আমরা জানি, 2s = a + b + c
বা, 84 = 25 + 27 + c
বা, 84 = 52 + c
বা, c = 84 – 52
∴ c = 32
ত্রিভুজটির অপর বাহুর দৈর্ঘ্য AB = c = 32 সে. মি.

∴ ΔABC এর ক্ষেত্রফল

\[\begin{array}{l}
{\rm{ = }}\sqrt {s(s – a)(s – b)(s – c)} \\
{\rm{ = }}\sqrt {42(42 – 25)(42 – 27)(42 – 32)} \\
{\rm{ = }}\sqrt {42 \times 17 \times 15 \times 10} \\
{\rm{ = }}\sqrt {107100}
\end{array}\]

= 327.26 বর্গ সে.মি.
অতএব, ত্রিভুজটির ক্ষেত্রফল 327.26 বর্গ সে. মি. (প্রায়) (Ans)

প্রশ্ন \ 5 \ একটি সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য 2 মিটার বাড়ালে এর ক্ষেত্রফল ${\rm{6}}\sqrt {\bf{3}}$ বর্গমিটার বেড়ে যায়। ত্রিভুজটির বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান : মনে করি, সমবাহু ত্রিভুজটির প্রত্যেক বাহুর দৈর্ঘ্য = a মিটার।
অতএব, সমবাহু ত্রিভুজক্ষেত্রের ক্ষেত্রফল = $\frac{{\sqrt 3 {a^2}}}{4}$ বর্গমিটার।
প্রত্যেক বাহুর দৈর্ঘ্য 2 মিটার বাড়ালে ত্রিভুজক্ষেত্রের ক্ষেত্রফল হবে
= $\frac{{\sqrt 3 {{(a + 2)}^2}}}{4}$ বর্গমিটার = $\frac{{\sqrt 3 ({a^2} + 4a + 4)}}{4}$ বর্গমিটার
∴ প্রশ্নানুসারে,

$\frac{{\sqrt 3 ({a^2} + 4a + 4)}}{4}{\rm{ = }}\frac{{\sqrt 3 {a^2}}}{4}{\rm{ + 6}}\sqrt 3$

বা, $\sqrt 3 {\rm{(}}{{\rm{a}}^{\rm{2}}}{\rm{ + 4a + 4) = }}\sqrt 3 {a^2}{\rm{ + 24}}\sqrt 3$

বা, a² + 4a + 4 = a² + 24
বা, a² + 4a – a² = 24 – 4
বা, 4a = 20
বা, ${\rm{a = }}\frac{{20}}{4}{\rm{ }}\therefore {\rm{ a = 5}}$

অতএব, সমবাহু ত্রিভুজটির প্রত্যেক বাহুর দৈর্ঘ্য 5 মিটার। (Ans)

প্রশ্ন \ 6 \ একটি ত্রিভুজের দুই বাহুর দৈর্ঘ্য যথাক্রমে 26 মিটার, 28 মিটার এবং ক্ষেত্রফল 182 বর্গমিটার হলে, বাহুদ্বয়ের অন্তর্ভুক্ত কোণ নির্ণয় কর।
সমাধান : মনে করি, ত্রিভুজের বাহুদ্বয় যথাক্রমে a = 26 মিটার ও b = 28 মিটার এবং ক্ষেত্রফল = 182 বর্গমিটার।

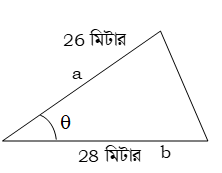
ধরি, বাহুদ্বয়ের অন্তর্ভুক্ত কোণ = θ
আমরা জানি,
ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2}{\rm{absin}}\theta$

বা, 182 = 1/2 × 26 × 28 × Sinθ

বা, 182 = 13 × 28 × Sinθ
বা, 182 = 364Sinθ
বা, 364Sinθ = 182
বা, Sinθ = 182/364 = 1/2 = Sin30°
∴ θ = 30°
সুতরাং বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 30° (Ans)

প্রশ্ন \ 7 \ একটি সমকোণী ত্রিভুজের লম্ব ভূমির 11/ 12 অংশ থেকে 6 সে.মি. কম এবং অতিভুজ ভূমির 4/3 অংশ থেকে 3 সে.মি. কম। ত্রিভুজটির ভূমির দৈর্ঘ্য নির্ণয় কর।
সমাধান : ABC সমকোণী ত্রিভুজের ∠B = সমকোণ

তাহলে BC ভূমি, AB লম্ব এবং AC অতিভুজ
মনে করি, ভূমি BC = x সে. মি.

শর্তানুযায়ী, লম্ব AB = x এর 11/12 – 6 সে. মি.
= 11x/12 – 6 সে. মি.

= $\left( {\frac{{11x - 72}}{{12}}} \right)$ সে. মি.

এবং অতিভুজ AC = x এর 4/3 – 3 সে. মি.
= 4x/3 – 3 সে. মি.

= $\left( {\frac{{4x - 9}}{3}} \right)$ সে.মি.
পিথাগোরাসের উপপাদ্য অনুযায়ী, AB2 + BC2 = AC2
বা, ${\left( {^{\frac{{11x - 72}}{{12}}}} \right)^{\rm{2}}}{\rm{ + }}{{\rm{x}}^{\rm{2}}}{\rm{ = }}{\left( {^{\frac{{4x - 9}}{3}}} \right)^{\rm{2}}}{\rm{ }}$

বা, $\frac{{121{x^2} - 1584x + 5184}}{{144}}{\rm{ + }}{{\rm{x}}^{\rm{2}}}{\rm{ = }}\frac{{16{x^2} - 72x + 81}}{9}$

বা, $\frac{{121{x^2} - 1584x + 5184 + 144{x^2}}}{{144}}{\rm{ = }}\frac{{16{x^2} - 72x + 81}}{9}$

বা, $\frac{{265{x^2} - 1584x + 5184}}{{16}}{\rm{ = 16}}{{\rm{x}}^{\rm{2}}}{\rm{ - 72x + 81}}$

বা, 265x²–1584x + 5184 = 256x²–1152x+ 1296
বা, 265x² – 256x² –1584x + 1152x + 5184 – 1296 = 0

বা, 9x² – 432x + 3888 = 0

বা, 9(x² – 48x + 432) = 0

বা, x² – 48x + 432 = 0

বা, x² – 36x – 12x + 432 = 0

বা, x(x – 36) – 12(x – 36) = 0

বা, (x – 36) (x – 12) = 0

হয়, x – 36 = 0 অথবা, x –12 = 0
∴ x = 36 ∴ x = 12
নির্ণেয় ত্রিভুজটির ভূমির দৈর্ঘ্য 36 সে. মি. অথবা 12 সে. মি.।

প্রশ্ন \ 8 \ একটি সমদ্বিবাহু ত্রিভুজের সমান সমান বাহুর দৈর্ঘ্য 10 মিটার এবং ক্ষেত্রফল 48 বর্গমিটার হলে, ভূমির দৈর্ঘ্য নির্ণয় কর।
সমাধান : মনে করি, সমদ্বিবাহু ত্রিভুজের সমান সমান বাহুর দৈর্ঘ্য ধ = 10 মিটার এবং ভূমির দৈর্ঘ্য ন মিটার।

∴ এর ক্ষেত্রফল = $\frac{b}{4}{\rm{ }}\sqrt {4{a^2} - {b^2}}$

প্রশ্নমতে, $\frac{b}{4}{\rm{ }}\sqrt {4{a^2} - {b^2}} {\rm{ = 48}}$

বা, $\frac{b}{4}{\rm{ }}\sqrt {4 \times {{(10)}^2} - {b^2}} = 48$

বা, $\frac{b}{4}\sqrt {4 \times 100 - {b^2}} {\rm{ = 48}}$

বা, ${\rm{b}}\sqrt {400 - {b^2}} {\rm{ = 192}}$

বা, b² (400 – b²) = 36864 [উভয়পক্ষকে বর্গ করে]

বা, 400b² – b⁴– 36864 = 0

বা, b⁴ – 400b²+ 36864 = 0

বা, b⁴ – 256b² – 144b² + 36864 = 0

বা, b²(b² – 256) -144(b² – 256) = 0

বা, (b² – 256) (b² – 144) = 0

হয়, b² – 256 = 0 অথবা, বা, b² – 144 = 0

বা, b² = 256 বা, b² = 144

বা, b² = (16)² বা, b² =(12)²

∴ b = 16 ∴ b = 12

নির্ণেয় সমবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 12 অথবা 16 মিটার।

প্রশ্ন \ 9 \ একটি নির্দিষ্ট স্থান থেকে দুইটি রাস্তা পরস্পর 135° কোণ করে দুইদিকে চলে গেছে। দুইজন লোক ঐ নির্দিষ্ট স্থান থেকে যথাক্রমে ঘণ্টায় 7 কিলোমিটার ও ঘণ্টায় 5 কিলোমিটার বেগে বিপরীত মুখে রওনা হলো। 4 ঘণ্টা পর তাদের মধ্যে সরাসরি দূরত্ব নির্ণয় কর।
সমাধান :
মনে করি, A থেকে দুইজন লোক যথাক্রমে ঘণ্টায় 7 কি. মি. ও ঘণ্টায় 5 কি. মি. বেগে রওনা হয়ে 4 ঘণ্টা পর B ও C বিন্দুতে এসে পৌঁছাল। তাহলে 4 ঘণ্টা পর তাদের মধ্যে সরাসরি দূরত্ব হবে BC.

C থেকে BA বাহুর বর্ধিতাংশের ওপর CD লম্ব টানি।
তাহলে, AB= 7 × 4 কি. মি. = 28 কি. মি.
AC = 5 × 4 কি. মি. = 20 কি. মি.
∠BAC = 135°
অতএব, ∠CAD = 45°
এখন, ACD সমকোণী ত্রিভুজ থেকে পাই,
CD/AC = Sin45° এবং AD/AC = Cos45°
∴ CD = AC. Sin45°

= ${\rm{20 }} \times {\rm{ }}\frac{1}{{\sqrt 2 }}{\rm{ = 10 }} \times {\rm{ }}\sqrt 2 \sqrt 2 {\rm{ }} \times {\rm{ }}\frac{1}{{\sqrt 2 }}{\rm{ = 10}}\sqrt 2$

এবং AD = AC Cos45°

= ${\rm{20 }} \times {\rm{ }}\frac{1}{{\sqrt 2 }}{\rm{ = 10 }} \times {\rm{ }}\sqrt 2 \sqrt 2 {\rm{ }} \times {\rm{ }}\frac{1}{{\sqrt 2 }}{\rm{ = 10}}\sqrt 2$
অতএব, cBDসমকোণী ত্রিভুজ থেকে পাই,

BC² = BD² + CD² = (BA + AD)² + CD²

= (28 + 10√2)² + (10√2)²

= (28 + 14.14)² + (10)²

= (42.14)² + (10√2)²

= 1775.78 + 200 = 1975.78

∴ BC = $\sqrt {1975.78}$

= 44.44 (প্রায়)
অতএব, দুইজন লোকের মধ্যে সরাসরি দূরত্ব 44.44 কি. মি. (প্রায়) (Ans)

প্রশ্ন \ 10 \ একটি সমবাহু ত্রিভুজের অভ্যন্তরস্থ একটি বিন্দু থেকে বাহু তিনটির ওপর অঙ্কিত লম্বের দৈর্ঘ্য যথাক্রমে 6 সে.মি., 7 সে.মি. ও 8 সে.মি.। ত্রিভুজটির বাহুর দৈর্ঘ্য এবং ক্ষেত্রফল নির্ণয় কর।
সমাধান :
মনে করি, ABC সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য = a সে.মি.
ত্রিভুজের অভ্যন্তরে O বিন্দু হতে বাহুগুলোর উপর লম্বের দৈর্ঘ্য যথাক্রমে OE = 6 সে.মি., OF = 7 সে.মি. এবং OD = 8 সে.মি.।

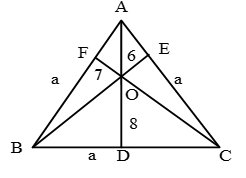
এখন O হতে কৌণিক বিন্দুগুলো যোগ করে তিনটি ত্রিভুজ ক্ষেত্রে ভাগ করা হলো।
Δ ক্ষেত্র AOB এর ক্ষেত্রফল
= 1/2 × ভূমি × উচ্চতা

= 1/2 a × OF
= a/2 × 7 বর্গ সে.মি.

= 7a/2 বর্গ সে.মি.

Δ ক্ষেত্র AOC এর ক্ষেত্রফল = 1/2 a × OE
= a/2 × 6 বর্গ সে.মি.
= 3a বর্গ সে.মি.

Δক্ষেত্র BOC এর ক্ষেত্রফল = 1/2 a × OD
= 12 a × 8 বর্গ সে.মি.
= 4a বর্গ সে.মি.

আমরা জানি, সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{{\sqrt 3 {a^2}}}{4}$
সুতরাং Δ ক্ষেত্র ABC এর ক্ষেত্রফল = $\frac{{\sqrt 3 {a^2}}}{4}$
প্রশ্নমতে, $\frac{{\sqrt 3 }}{4}{\rm{ }}{{\rm{a}}^{\rm{2}}}{\rm{ = }}\frac{{7a}}{2}{\rm{ + 3a + 4a}}$

বা, $\frac{{\sqrt 3 }}{4}{\rm{ }}{{\rm{a}}^{\rm{2}}}{\rm{ = a }}\left( {\begin{array}{ccccccccccccccc} {\frac{7}{2} + 3 + 4} \end{array}} \right)$

বা, $\frac{{\sqrt 3 }}{4}{\rm{a = }}\frac{7}{2}{\rm{ + 7 }}$ [উভয়পক্ষকে a দ্বারা ভাগ করে]
বা, $\frac{{\sqrt 3 }}{4}{\rm{ a = }}\frac{{7 + 14}}{2}{\rm{ }}$

বা, $\sqrt 3 {\rm{a = }}\frac{{21 \times 4}}{2}$

বা, $\sqrt 3 {\rm{a = 42}}$

বা, ${\left( {^{\sqrt 3 a}} \right)^{\rm{2}}} = {\left( {42} \right)^2}\;\;\;\;$ [উভয়পক্ষকে বর্গ করে]
বা, 3a² = 1764
বা, ${{\rm{a}}^{\rm{2}}}{\rm{ = }}\frac{{1764}}{3}{\rm{ = 588}}$

বা, ${\rm{a = }}\sqrt {588}$

${\rm{ = }}\sqrt {196 \times 3} {\rm{ = }}\sqrt {(14)2 \times 3}$

∴ a = 14 √3 সে.মি.
= 24.249 সে.মি. (প্রায়)
প্রত্যেক বাহুর দৈর্ঘ্য 24.249 সে.মি. (প্রায়)
এবং ক্ষেত্রফল = $\frac{{\sqrt 3 {a^2}}}{4}$ = $\frac{{\sqrt 3 }}{4}(588)$