এসএসসি সাধারণ গণিত ১৬.৩ অনুশীলনীর প্রশ্ন ও সমাধান

নবম-দশম শ্রেণির বা এসএসসি সাধারণ গণিত ১৬.৩ অনুশীলনীর প্রশ্ন ও সমাধান পেতে সম্পূর্ণ পোস্টটি পড়ুন। বহুনির্বাচনী ও সৃজনশীল প্রশ্ন ও সমাধানের লিংক নিচে দেওয়া হবে।

সাধারণ গণিত ১৬.৩ অনুশীলনীর প্রশ্ন ও সমাধান

পাঠ সম্পর্কিত সূত্রাবলী

⇒ বৃত্ত সংক্রান্ত পরিমাপ :
বৃত্তের পরিধি = 2Πr = 3.1416………..

⇒ বৃত্তাংশের দৈর্ঘ্য
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ r এবং AB = S বৃত্তচাপ কেন্দ্রে θ° কোণ উৎপন্ন করে।
∴ বৃত্তের পরিধি = 2Πr

বৃত্তের কেন্দ্রে মোট উৎপন্ন কোণ = 360° এবং চাপ S দ্বারা কেন্দ্রে উৎপন্ন কোণের ডিগ্রী পরিমাণ θ°
আমরা জানি, বৃত্তের কোনো চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ ঐ বৃত্তচাপের সমানুপাতিক।
∴ $\frac{\theta }{{360^\circ }}{\rm{ = }}\frac{S}{{2\pi r}}{\rm{ }}$

বা, ${\rm{S = }}\frac{{\pi r\theta }}{{180}}$

⇒ বৃত্তক্ষেত্র ও বৃত্তকলার ক্ষেত্রফল:

বৃত্তকলার ক্ষেত্রফল = $\frac{\theta }{{360^\circ }}{\rm{ }} \times {\rm{ }}\pi {{\rm{r}}^{\rm{2}}}$

নবম-দশম শ্রেণির ১৬.৩ অনুশীলনীর প্রশ্ন ও সমাধান

প্রশ্ন \ 1 \ একটি বৃত্তচাপ কেন্দ্রে 30° কোণ উৎপন্ন করে। বৃত্তের ব্যাস 126 সে. মি. হলে, চাপের দৈর্ঘ্য নির্ণয় কর।
সমাধান : বৃত্তের চাপের ডিগ্রি পরিমাপ, x = 30°
বৃত্তের ব্যাসার্ধ, r = ব্যাস÷2 = 126÷2 সে. মি. = 63 সে. মি.
মনে করি, বৃত্তচাপের দৈর্ঘ্য = ‍S সে. মি.
আমরা জানি, S = $\frac{{\pi rx}}{{180^\circ }}$

= $\frac{{3.1416 \times 63 \times 30^\circ }}{{180^\circ }}$ সে. মি. [∵ Π = 3.1416]
= 32.987 সে. মি. (প্রায়)
নির্ণেয় বৃত্তচাপের দৈর্ঘ্য 32.987 সে. মি. (প্রায়)।

প্রশ্ন \ 2 \ প্রতি মিনিটে 66 মিটার বেগে 112 মিনিটে একটি ঘোড়া কোনো মাঠ ঘুরে এলো। ঐ মাঠের ব্যাস নির্ণয় কর।
সমাধান : দেওয়া আছে, বেগ = 66 মিটার/মিনিট
এবং সময় = 1 $\frac{1}{2}$ মিনিট = $\frac{3}{2}$ মিনিট
ঘোড়াটি 1 মিনিটে যায় 66 মিটার
∴ $\frac{3}{2}$ মিনিটে যায় = 66 × $\frac{3}{2}$ মিটার = 99 মিটার
বৃত্তের ব্যাসার্ধ r মিটার হলে, ব্যাস = 2r মিটার এবং পরিধি = 2Πr মিটার
শর্তানুসারে, 2Πr = 99
বা, 2r = 99÷Π = 99÷3.1416 = 31.512605 = 31.513 মিটার (প্রায়)
নির্ণেয় মাঠের ব্যাস 31.513 মিটার (প্রায়)।

প্রশ্ন \ 3 \ একটি বৃত্তাংশের ক্ষেত্রফল 77 বর্গমিটার এবং বৃত্তের ব্যাসার্ধ 21 মিটার। বৃত্তচাপটি কেন্দ্রে যে কোণ উৎপন্ন করে, তা নির্ণয় কর।
সমাধান :

নবম-দশম শ্রেণির ১৬.৩ অনুশীলনীর প্রশ্ন ও সমাধান

আমরা জানি, বৃত্তাংশের ক্ষেত্রফল = $\frac{\theta }{{360^\circ }}{\rm{ }} \times {\rm{ }}\pi {{\rm{r}}^{\rm{2}}}$ বর্গ একক
যেখানে বৃত্তের ব্যাসার্ধ = r এবং চাপের ডিগ্রি পরিমাপ = θ
প্রশ্নমতে, 77 = $\frac{\theta }{{360}}{\rm{ }} \times {\rm{ 3}}{\rm{.1416 }} \times {\rm{ (21}}{{\rm{)}}^{\rm{2}}}$

বা, θ = $\frac{{360 \times 77}}{{3.1416 \times 21 \times 21}}$ = 20.008

নির্ণেয় কোণ 20.008°

প্রশ্ন \ 4 \ একটি বৃত্তের ব্যাসার্ধ 14 সে. মি. এবং বৃত্তচাপ কেন্দ্রে 75° কোণ উৎপন্ন করে। বৃত্তাংশের ক্ষেত্রফল নির্ণয় কর।
সমাধান : দেওয়া আছে, বৃত্তের ব্যাসার্ধ, r = 14 সে. মি.
বৃত্তাংশের কেন্দ্রে উৎপন্ন কোণের পরিমাপ, θ = 75°
আমরা জানি, বৃত্তাংশের ক্ষেত্রফল = $\frac{\theta }{{360^\circ }}{\rm{ }} \times {\rm{ }}\pi {{\rm{r}}^{\rm{2}}}$ বর্গ একক
= $\frac{{75}}{{360}}{\rm{ }} \times {\rm{ 3}}{\rm{.1416 }} \times {\rm{ (14}}{{\rm{)}}^{\rm{2}}}{\rm{ }}$ বর্গ সে.মি.

= $\frac{{5 \times 3.1416 \times 14 \times 14}}{{24}}$ বর্গ সে.মি.

= $\frac{{5 \times 3.1416 \times 49}}{6}$ বর্গ সে.মি.
= 5 × 0.5236 × 49 বর্গ সে.মি.
= 128.282 বর্গ সে. মি. (প্রায়)
নির্ণেয় বৃত্তাংশের ক্ষেত্রফল 128.282 বর্গ সে.মি. (প্রায়)।

প্রশ্ন \ 5 \ একটি বৃত্তাকার মাঠকে ঘিরে একটি রাস্তা আছে। রাস্তাটির ভিতরের পরিধি অপেক্ষা বাইরের পরিধি 44 মিটার বড়। রাস্তাটির চওড়া নির্ণয় কর।
সমাধান : মনে করি, বাইরের বৃত্তের ব্যাসার্ধ, OB = R মি. এবং ভেতরের বৃত্তের ব্যাসার্ধ, OA = r মি.

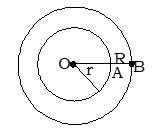
তাহলে, রাস্তাটির বিস্তার = (R – r) মি.
জ ব্যাসার্ধবিশিষ্ট বৃত্তের পরিধি = 2Πজ মি.

এবং R ব্যাসার্ধবিশিষ্ট বৃত্তের পরিধি = 2Πr মি.
প্রশ্নমতে, 2ΠR – 2Πr = 44
বা, 2Π (R – ৎ) = 44
বা, R – r = 44÷2Π = 44÷(2 × 3.1416) = 22÷3.1416
= 7.0028011
= 7.002 (প্রায়)
নির্ণেয় রাস্তাটি 7.002 মিটার চওড়া (প্রায়)।

প্রশ্ন \ 6 \ একটি বৃত্তাকার পার্কের ব্যাস 26 মিটার। পার্কটিকে বেষ্টন করে বাইরে 2 মিটার প্রশস্ত একটি পথ আছে। পথটির ক্ষেত্রফল নির্ণয় কর।
সমাধান : মনে করি, ঙ কেন্দ্রবিশিষ্ট একটি বৃত্তাকার পার্কের ব্যাস AB এবং পার্কটিকে বেষ্টন করে BF প্রশস্ত একটি পথ বিদ্যমান।

দেওয়া আছে, বৃত্তাকার পার্কের ব্যাস,
AB = 26 মিটার

এবং পথটির প্রশস্ততা, BF = 2 মিটার
বৃত্তাকার পার্কের ব্যাসার্ধ, r₁ = AB÷2 = 26÷2 মি. = 13 মি.
এবং পার্কসহ পথ দ্বারা গঠিত বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ,
r₂ = OB + 2 = (13 + 2) মিটার = 15 মিটার
এখন, জানা আছে, যেকোনো বৃত্তের ক্ষেত্রফল Πr² বর্গ একক
যেখানে r = উক্ত বৃত্তের ব্যাসার্ধ এবং Π = 3.1416
∴ বৃত্তাকার পার্কের ক্ষেত্রফল , A₁ = Πr₁² বর্গ মি.
= 3.1416 × (13)² বর্গ মি.
= 530.93 বর্গ মি.
এবং পার্কসহ পথ দ্বারা গঠিত বৃত্তের ক্ষেত্রফল,
A2 = Πr₂² বর্গ মি.
= 3.1416 × (15)² বর্গ মি.
= 706.86 বর্গ মি.
অতএব, পথটির ক্ষেত্রফল = (A₂ – A1) বর্গমি.
= (706.86 – 530.93) বর্গমি.
= 175.93 বর্গ.মি. (প্রায়)
নির্ণেয় পথের ক্ষেত্রফল 175.93 বর্গমি. (প্রায়)।

প্রশ্ন \ 7 \ একটি গাড়ির সামনের চাকার ব্যাস 28 সে.মি. এবং পিছনের চাকার ব্যাস 35 সে.মি.। 88 মিটার পথ যেতে সামনের চাকা পিছনের চাকা অপেক্ষা কত পূর্ণসংখ্যক বার বেশি ঘুরবে?
সমাধান :
গাড়ির সামনের চাকার ব্যাসার্ধ= 28÷2 সে.মি. = 14 সে.মি.
গাড়ির পিছনের চাকার ব্যাসার্ধ= 35÷2 সে.মি.
অতএব, গাড়ির সামনের চাকার পরিধি = 2 × 3.1416 ×14 সে.মি.
= 87.9648 সে.মি. (প্রায়)
এবং গাড়ির পিছনের চাকার পরিধি = 2 × 3.1416 × 35÷2 সে.মি.
= 109.956 সে.মি.
এখন, 88 মি. = 88 × 100 সে.মি.
সুতরাং 88 মিটার পথ যেতে গাড়ির সামনের চাকা ঘুরবে $\frac{{88 \times 100}}{{87.9648}}$ বার
= 100.04 বার
= 100 বার (প্রায়)
এবং গাড়ির পিছনের চাকা ঘুরবে $\frac{{88 \times 100}}{{109.956}}$ বার = 80.032 বার
= 80 বার (প্রায়)
অতএব, সামনের চাকা পিছনের চাকা অপেক্ষা (100 – 80)
বা, 20 বার বেশি ঘুরবে। (Ans)

প্রশ্ন \ 8 \ একটি বৃত্তের পরিধি 220 মিটার। ঐ বৃত্তে অন্তর্লিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান :

মনে করি, বৃত্তের ব্যাসার্ধ= r মিটার
বৃত্তের পরিধি = 2Πr একক।
প্রশ্নানুসারে, 2Πr = 220
বা, 2 × 3.1416 × r = 220
বা, 6.2832r = 220

বা, r = 35.014
∴ বৃত্তের ব্যাসার্ধ= 35.014 মিটার
বৃত্তের ব্যাস AC = 2 × 35.014 মি. = 70.028 মিটার (প্রায়)
এখন, ABC সমকোণী সমদ্বিবাহু ত্রিভুজ থেকে আমরা পাই,
AB² + BC² = AC²
বা, 2AB² = AC², [∵ BC = AB]
বা, √2 AB = AC
বা, AB = $\frac{1}{{\sqrt 2 }}$ × 70.028 = 49.5173 মিটার
∴ বৃত্তে অন্তর্লিখিত বাহুর দৈর্ঘ্য 49.517 মিটার (প্রায়)। (Ans)

প্রশ্ন \ 9 \ একটি বৃত্তের পরিধি একটি সমবাহু ত্রিভুজের পরিসীমার সমান। এদের ক্ষেত্রফলের অনুপাত নির্ণয় কর।
সমাধান : মনে করি, বৃত্তের ব্যাসার্ধ= r
অতএব, বৃত্তক্ষেত্রের ক্ষেত্রফল = Πr² এবং বৃত্তের পরিধি = 2Πr
প্রশ্নানুসারে, সমবাহু ত্রিভুজের পরিসীমা = 2Πr
∴ এক বাহুর দৈর্ঘ্য, a= $\frac{{2\pi r}}{3}$

এখন, ত্রিভুজক্ষেত্রের ক্ষেত্রফল = $\frac{{\sqrt 3 }}{4}{{\rm{a}}^{\rm{2}}}{\rm{ }}$ বর্গ একক
= $\frac{{\sqrt 3 }}{4}{\rm{ }}{\left( {\frac{{2\pi r}}{3}} \right)^2}$ বর্গ একক = ${\frac{{\sqrt 3 }}{4}^{\rm{.}}}{\rm{ }}\frac{{4{\pi ^2}{r^2}}}{9}$ বর্গ একক
= $\frac{{{\pi ^2}{r^2}}}{{3\sqrt 3 }}$ বর্গ একক
অতএব, বৃত্তক্ষেত্রের ক্ষেত্রফল ঃ সমবাহু ত্রিভুজক্ষেত্রের ক্ষেত্রফল = $\pi {{\rm{r}}^{\rm{2}}}{\rm{ : }}\frac{{{\pi ^2}{r^2}}}{{3\sqrt 3 }}$

= 3√3 : Π (Ans)

প্রশ্ন \ 10 \ নিচের চিত্রের তথ্য অনুযায়ী গাঢ় চিহ্নিত ক্ষেত্রগুলোর ক্ষেত্রফল নির্ণয় কর :

সমাধান :

1ম চিত্রে :

ΔABC এর পরিসীমা, 2s = 10 + 9 + 8
বা, 2s = 27
∴ s = 13.5
∴ ΔABC এর ক্ষেত্রফল = $\sqrt {s(s - a)(s - b)(s - c)}$ বর্গ সে.মি.
= $\sqrt {13.5(13.5 - 10)(13.5 - 9)(13.5 - 8)}$ বর্গ সে.মি.
= $\sqrt {(13.5 \times 3.5 \times 4.5 \times 5.5)}$ বর্গ সে.মি.
= $\sqrt {1169.4375}$ বর্গ সে.মি.
= 34.197 বর্গ সে.মি.

ADB অর্ধবৃত্তের ক্ষেত্রফল = $\frac{1}{2}\pi {\left( {\frac{9}{2}} \right)^2}$ বর্গ সে.মি. [∵ r = 9/2 ]
= $\frac{1}{2}$ × 3.1416 × 20.25 বর্গ সে.মি.
= 31.809 বর্গ সে.মি.
∴ ACBD ক্ষেত্রের ক্ষেত্রফল = ΔABC এর ক্ষেত্রফল + ADB অর্ধবৃত্তের ক্ষেত্রফল = (34.197 + 31.809) বর্গ সে.মি.
= 66.006 বর্গ সে.মি. (প্রায়) (Ans)

2য় চিত্রে :

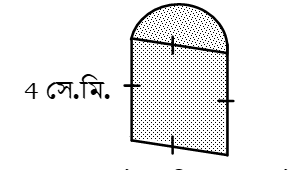
ABCD বর্গক্ষেত্রের ক্ষেত্রফল =(4)² বর্গ সে.মি.= 16 বর্গ সে.মি.
এবং উঊc অর্ধবৃত্তের ক্ষেত্রফল = $\frac{1}{2}\pi {\left( {\frac{4}{2}} \right)^2}$ বর্গ সে.মি. [∵ r = 42 ]
= $\frac{1}{2}$ × 3.1416 × 4 বর্গ সে.মি.
= 6.283 বর্গ সে.মি.
∴ গাঢ় চিহ্নিত অংশের ক্ষেত্রফল
= ABCD এর ক্ষেত্রফল + উঊc এর ক্ষেত্রফল
= (16 + 6.283) বর্গ সে.মি.
= 22.283 বর্গ সে.মি. (প্রায়) (Ans)

3য় চিত্রে :

ABCD আয়তক্ষেত্রের ক্ষেত্রফল = (12 × 10) বর্গ সে.মি.
= 120 বর্গ সে.মি.
AEB অর্ধবৃত্তের ক্ষেত্রফল ${\rm{ = }}\frac{1}{2}\pi {\rm{ }}{\left( {\frac{{12}}{2}} \right)^2}$ বর্গ সে.মি. ∵r = 12/2
= $\frac{1}{2}$ × 3.1416 × 36 বর্গ সে.মি. = 56.549 বর্গ সে.মি.
∴ গাঢ় চিহ্নিত অংশে ক্ষেত্রফল = (120 – 56.549) বর্গ সে.মি.
= 63.451 বর্গ সে.মি. (প্রায়) (Ans)

4র্থ চিত্রে :

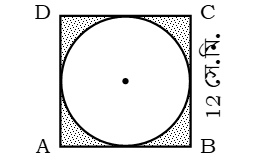
12 সে.মি. বাহুবিশিষ্ট বর্গক্ষেত্রের ক্ষেত্রফল = (12)² বর্গ সে.মি.
= 144 বর্গ সে.মি.
যেহেতু বৃত্তটি বর্গের মধ্যে ঠিকভাবে এঁটে যায়,
∴ বৃত্তের ব্যাসার্ধ= 12/2 সে.মি. = 6 সে.মি.
∴ বৃত্তের ক্ষেত্রফল = Π(6)² বর্গ সে.মি. = 3.1416 × 36 বর্গ সে.মি.
= 113.097 বর্গ সে.মি
∴ গাঢ় চিহ্নিত অংশের ক্ষেত্রফল = (144 – 113.097) বর্গ সে.মি.
= 30.903 বর্গ সে.মি. (প্রায়) (Ans)

🔶🔶 এসএসসি সাধারণ গণিত ১৬.১ অনুশীলনী

🔶🔶 এসএসসি সাধারণ গণিত ১৬.২ অনুশীলনী

🔶🔶 এসএসসি সাধারণ গণিত ১৬.৪ অনুশীলনী

🔶🔶 এসএসসি সাধারণ গণিত সকল অধ্যায়