নবম-দশম শ্রেণির গণিত দ্বিতীয় অধ্যায়ঃ সেট ও ফাংশন অনুশীলনী- ২.১ সেট SSC Math Chapter 2.1 Set

নবম-দশম শ্রেণির গণিত দ্বিতীয় অধ্যায়ঃ সেট ও ফাংশন অনুশীলনী- ২.১ সেট SSC Math Chapter 2.1 Set পোস্টে সকলকে স্বাগতম। আজকে গণিত সেট অধ্যায়ের অনুশীলনির প্রশ্ন ও উত্তর গুলো দেওয়া হবে। নবম-দশম বা এসএসসি পরীক্ষার্থীদের জন্য সাধারণ গণিত দ্বিতীয় অধ্যায় সেট ও ফাংশন এর অনুশীলনীর প্রশ্ন গুলো খুবই গুরুত্বপূর্ণ। ২.১ সেট অনুশীলনীর প্রশ্নগুলো অনুশীলন করলে সৃজনশীল অংশ খুব সহজ হয়ে যাবে।

নবম-দশম শ্রেণির গণিত অনুশীলনী- ২.১ সেট

প্রশ্ন ১ নিচের সেটগুলোকে তালিকা পদ্ধতিতে প্রকাশ কর :

(ক) {x ∈ N : x² > 9 এবং x³ < 130}

সমাধান : যে সকল স্বাভাবিক সংখ্যার বর্গ ৯ অপেক্ষা বড় এবং ঘন ১৩০ অপেক্ষা ছোট তাদের সেট।

আমরা জানি, স্বাভাবিক সংখ্যার সেট N = {1, 2, 3, 4, 5, 6, ……..}

এখানে,

x = 1 হলে, x² = 1²= 1⊁9 এবং x³ = 1³ = 1 < 130

x = 2 হলে, x² = 2² = 4⊁9 এবং x³ = 2³ = 8 < 130

x = 3 হলে, x² = 3² = 9 ≥9 এবং x³ = 3³ = 27 < 130

x = 4 হলে, x² = 4² = 16 > 9 এবং x³ = 4³ = 64 < 130

x = 5 হলে, x² = 5² = 25 > 9 এবংx³ = 5³= 125< 130

x = 6হলে x² = 6² = 36 > 9 এবং x³= 6³ = 216 ⊀ 130

∴ শর্তানুসারে গ্রহণযোগ্য সংখ্যাগুলো 4, 5

∴ নির্ণেয় সেট = {4, 5}

$ads={1}

(খ) {x ∈ Z : x² > 5 এবং x² £ 36}

সমাধান : যে সকল পূর্ণসংখ্যার বর্গ 5 অপেক্ষা বড় এবং 35 অপেক্ষা বড় নয় তাদের সেট।

আমরা জানি, পূর্ণসংখ্যার সেট Z = {. . . . – 3, – 2, – 1, 0, 1, 2, 3 . . . . . }

এখানে,

x = 0 হলে, x²= 0² = 0 ⊁5 এবং 0 < 36

x = ±1 হলে, x² = (±1)² = 1 ⊁5 এবং 1 < 36

x = ±2 হলে, x² = (±2)² = 4⊁5 এবং 4 < 36

x = ±3 হলে, x² = (±3)² = 9 > 5 এবং 9 < 36

x = ±4 হলে, x² = (±4)² = 16 > 5 এবং 16 < 36

x = ±5 হলে, x²= (±5)² = 25 > 5 এবং 25 < 36

x = ±6 হলে, x²= (±6)² = 36 > 5 এবং 36 = 36

x = ±7 হলে, x²= (±7)² = 49 > 5 এবং 49 ⊀ 36

…………………………………………………

∴শর্তানুসারে গ্রহণযোগ্য সংখ্যাসমূহ: ±3, ±4, ±5, ±6

নির্ণেয় সেট = {± 3, ±4, ±5, ±6}

(গ){x ∈ N : x, 36 এর গুণনীয়ক এবং 6 এর গুণিতক }

সমাধান : যে সকল স্বাভাবিক সংখ্যা ৩৬ এর গুণনীয়ক এবং ৬ এর গুণিতক তাদের সেট।

আমরা জানি, স্বাভাবিক সংখ্যা সেট N = (1, 2, 3, 4, 5, . . . . .. )

এখানে, 36 = 1×36

= 2 ×18

= 3×12

= 4×9

= 6×6

∴ 36 এর গুণনীয়কসমূহ 1, 2, 3, 4, 6, 9, 12, 18, 36

এবং 6 এর গুণিতকসমূহ 6, 12, 18, 24, 30, 36 . . . . . .

∴36 এর গুণনীয়ক এবং 6 এর গুণিতকগুলো হলো যথাক্রমে 6, 12, 18, 36

নির্ণেয় সেট = {6, 12, 18, 36}

(ঘ) {x ∈ N : x³ > 25 এবং x⁴ < 264}

সমাধান : যেসকল স্বাভাবিক সংখ্যার ঘন 25 অপেক্ষা ছোট এবং চতুর্ঘাত 264 অপেক্ষা ছোট তাদের সেট।

আমরা জানি,

স্বাভাবিক সংখ্যার সেট, N = (1, 2, 3, 4, 5, 6, . . . . . }

এখানে,

x = 1 হলে,x³ = 1³ = 1⊁25 এবং x⁴ = 1⁴= 1 < 264

x = 2হলে,x³ = 2³ = 8⊁25 এবং x⁴ = 2⁴= 16 < 264

x = 3 হলে,x³ = 3³ = 27 > 25 এবং x⁴ = 3⁴= 81< 264

x = 4 হলে,x³= 4³ = 64 > 25 এবং x⁴ = 4⁴= 256 < 264

x = 5 হলে,x³= 5³ = 125 > 25 এবং x⁴ = 5⁴= 625 ⊀264

…………………………………………………

∴ শর্তানুসারে গ্রহণযোগ্য স্বাভাবিক সংখ্যাসমূহ 3, 4

নির্ণেয় সেট = {3, 4}

$ads={1}

প্রশ্ন ২ নিচের সেটগুলোকে সেট গঠন পদ্ধতিতে প্রকাশ কর:

(ক) {3, 5, 7, 9, 11}

সমাধান : প্রদত্ত সেটের উপাদানসমূহ 3, 5, 7, 9, 11

এখানে, প্রত্যেকটি উপাদান স্বাভাবিক বিজোড় সংখ্যা যা 1 থেকে বড় এবং 13 থেকে ছোট।

নির্ণেয় সেট = {x ∈ N : x বিজোড় সংখ্যা এবং 1＜x＜13}

(খ) {1, 2, 3, 4, 6, 9, 12, 18, 36}

সমাধান : প্রদত্ত সেটের উপাদানসমূহ 1, 2, 3, 4, 6, 9, 12, 18, 36

এখানে, প্রত্যেকটি উপাদান স্বাভাবিক সংখ্যা এবং 36 এর গুণনীয়ক।

নির্ণেয় সেট = {x ∈N : x, 36 এর গুণনীয়ক}

গ) {4,8,12,16,20,24,28,32,36,40}

সমাধান : প্রদত্ত সেটের উপাদানসমূহ 4,8,12,16,20,24,28,32,36,40

এখানে, প্রত্যেকটি উপাদান 4 দ্বারা বিভাজ্য, অর্থাৎ 4 এর গুণিতক এবং 40 এর বড় নয়।

নির্ণেয় সেট = {x ∈ N : x, 4 এর গুণিতক এবং x ≤ 40}

(ঘ) {± 4, ± 5, ± 6}

সমাধান : প্রদত্ত সেটের উপাদানসমূহ – 6, – 5, – 4, 4, 5, 6

এখানে, প্রত্যেকটি উপাদান পূর্ণসংখ্যা। বর্গ 16 অপেক্ষা ছোট নয় এবং ঘন 216 অপেক্ষা বড় নয়।

নির্ণেয় সেট = {x ∈ Z : x² ≥16 এবং x³ ≤ 216}

প্রশ্ন ৩ A = {2, 3, 4}, B = {1, 2, a} এবং C = {2, a, b} হলে, নিচের সেটগুলো নির্ণয় কর।

(ক) BC

সমাধান : দেওয়া আছে, B = {1, 2, a}

এবং C = {2, a, b}

∴ B C = {1, 2, a} {2, a, b}

= {1} (Ans.)

(খ) A ∪ B

সমাধান : দেওয়া আছে, A = {2, 3, 4}

এবং B = {1, 2, a}

∴ A ∪ B = {2, 3, 4} ∪ {1, 2, a}

= {1, 2, 3, 4, a} (Ans.)

(গ) A ∩ C

সমাধান : দেওয়া আছে, A = {2, 3, 4}

এবং C = {2, a, b}

∴ A ∩ C = {2, 3, 4} ∩ {2, a, b}

= {2} (Ans.)

(ঘ) A ∪ (B ∩ C)

সমাধান : দেওয়া আছে, A = {2, 3, 4}, B = {1, 2, a}

এবং C = {2, a, b}

এখন, B ∩ C = {1, 2, a} ∩ {2, a, b} = (2, a)

∴A ∪ (B ∩ C) = {2, 3, 4} ∪ {2, a}

= {2, 3, 4, a} (Ans.)

(ঙ) A ∩ (B ∪ C)

সমাধান : দেওয়া আছে, A = {2, 3, 4}, B = {1, 2, a}

এবং C = {2, a, b}

এখন, B ∪ C = {1, 2, a} ∪ {2, a, b} = (1, 2, a, b)

∴ A ∩ (B ∪ C) = {2, 3, 4} ∩ {1, 2, a, b} = {2} (Ans.)

প্রশ্ন ৪ U = {1, 2, 3, 4, 5, 6, 7}, A = {1, 3, 5}, B = {2, 4, 6} এবং C = {3, 4, 5, 6, 7} হলে, নিম্নলিখিত ক্ষেত্রে সত্যতা যাচাই কর :

(i) (A ∪ B)’= A‘∩ B‘

সমাধান : দেওয়া আছে, U = {1, 2, 3, 4, 5, 6, 7},

A = {1, 3, 5} এবং B = {2, 4, 6}

এখন, A ∪ B = {1, 3, 5} ∪ {2, 4, 6}

= {1, 2, 3, 4, 5, 6}

∴বামপক্ষ = (A ∪ B)‘ = U {A ∪ B}

= {1, 2, 3, 4, 5, 6, 7} {1, 2, 3, 4, 5, 6}

= {7}

আবার, A‘ = UA = {1, 2, 3, 4, 5, 6, 7} {1, 3, 5}

= {2, 4, 6, 7}

এবং B‘ = UB = {1, 2, 3, 4, 5, 6, 7}{2, 4, 6}

= {1, 3, 5, 7}

∴ডানপক্ষ = A¢ ∩ B¢ = {2, 4, 6, 7} ∩ {1, 3, 5, 7}

= {7}

অর্থাৎ (A ∪ B)‘ = A‘∩ B‘ (সত্যতা যাচাই করা হলো)

(ii) (B ∩ C)‘ = B‘ ∪ C‘

সমাধান : দেওয়া আছে, U = {1, 2, 3, 4, 5, 6, 7},

C = {3, 4, 5, 6, 7} এবং B = {2, 4, 6}

এখন, B ∩ C = {2, 4, 6} ∩ {3, 4, 5, 6, 7} = {4, 6}

∴বামপক্ষ = (B ∩ C)‘ = U(B ∩ C)

= {1, 2, 3, 4, 5, 6, 7}{4, 6}

= {1, 2, 3, 5, 7}

আবার, B‘= UB = {1, 2, 3, 4, 5, 6, 7}{2, 4, 6} = {1, 3, 5, 7}

এবং C‘ = UC = {1, 2, 3, 4, 5, 6, 7} {3, 4, 5, 6, 7} = {1, 2}

∴ ডানপক্ষ B‘ ∪ C‘ = {1, 3, 5, 7} ∪ {1, 2} = {1, 2, 3, 5, 7}

∴ বামপক্ষ = ডানপক্ষ

অর্থাৎ (B ∩ C)‘ = B‘ ∪ C‘ (সত্যতা যাচাই করা হলো)

(iii) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)

সমাধান : দেওয়া আছে, U = {1, 2, 3, 4, 5, 6, 7},

A = {1, 3, 5}, B = {2, 4, 6} এবং {3, 4, 5, 6, 7}

এখন, A ∪ B = {1, 3, 5} ∪ {2, 4, 6} = {1, 2, 3, 4, 5, 6}

∴ বামপক্ষ = (A ∪ B) ∩ C

= {1, 2, 3, 4, 5, 6} ∩ {3, 4, 5, 6, 7}

= {3, 4, 5, 6}

আবার, A ∩ C = {1, 3, 5} ∩ {3, 4, 5, 6, 7} = {3, 5}

এবং B ∩ C = {2, 4, 6} ∩ {3, 4, 5, 6, 7} = {4, 6}

∴ ডানপক্ষ = (A ∩ C) ∪ (B ∩ C) = {3, 5} ∪ {4, 6}= {3, 4, 5, 6}

∴ বামপক্ষ = ডানপক্ষ

অর্থাৎ (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) (সত্যতা যাচাই করা হলো)

$ads={1}

(iv) (A ∩B) ∪ C = (A ∪ C) ∩ (B ∪ C)

সমাধান : দেওয়া আছে, U = {1, 2, 3, 4, 5, 6, 7},

A = {1, 3, 5}, B = {2, 4, 6} েএবং C = {3, 4, 5, 6, 7}

এখন, A ∩ B = {1, 3, 5} ∩ {2, 4, 6} = { }

∴ বামপক্ষ = (A ∩ B) ∪ C

= { } ∪ {3, 4, 5, 6, 7} = {3, 4, 5, 6, 7}

আবার, A ∪ C = {1, 3, 5} ∪ {3, 4, 5, 6, 7}

= {1, 3, 4, 5, 6, 7}

এবং B ∪ C = {2, 4, 6} ∪ {3, 4, 5, 6, 7}

= {2, 3, 4, 5, 6, 7}

∴ ডানপক্ষ = (A ∪ C) ∩ (B ∪ C)
= {1, 3, 4, 5, 6, 7} ∩ {2, 3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7}

অর্থাৎ (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) (সত্যতা যাচাই করা হলো)

প্রশ্ন ৫ Q = {x,y} এবং R = {m, n, l} হলে, P(Q) এবং P(R) নির্ণয় কর।

সমাধান : দেওয়া আছে, Q = {x,y} এবং R = {m, n, l}

Q সেটের উপসেটগুলো হলো {x, y}, {x}, {y}, f

∴ P (Q) = {{x, y}, {x}, {y}, f} (Ans.)

আবার, R সেটের উপসেটগুলো হলো {m, n, l}, {m, n}, {m, l}, {n, l}, {m}, {n}, {l} f

∴ P(R) = {{m, n, l}, {m, n} {m, l} {n, l}, {m}, {n}, {l}, f} (Ans.)

প্রশ্ন ৬ A = {a, b}, B = {a, b, c} এবং C = A È B হলে, দেখাও যে, P(C) এর উপাদান সংখ্যা 2ⁿ, যেখানে n হচ্ছে C এর উপাদান সংখ্যা।

সমাধান : দেওয়া আছে, A = {a, b}, B = {a, b, c} এবং C = A ∪ B

∴ C= A ∪ B = {a, b} ∪ {a, b, c} = {a, b, c}

এখন, C সেটের উপসেটগুলো হলো {a, b, c}, {a, b}, {b, c}, {a, c},{a}, {b}, {c}, f

∴ P(C) = {{a, b, c}, {a, b}, {b, c}, {a, c}, {a}, {b}, {c}, f}

∴ P(C) এর উপাদান সংখ্যা = 8 = 2³

∴ C সেটের উপাদান সংখ্যা হ হলে P(C) এর উপাদান সংখ্যা 2ⁿ(দেখানো হলো)

প্রশ্ন ৭ (ক) (x – 1, y + 2) = (y – 2, 2x + 1) হলে, x এবং y এর মান নির্ণয় কর।

সমাধান : দেওয়া আছে, (x – 1, y + 2) = (y – 2, 2x + 1)

ক্রমজোড়ের সংজ্ঞানুসারে,x – 1 = y – 2 . . . . . .. . . (i)

এবং y + 2 = 2x + 1 . . . . .. . (ii)

সমীকরণ (i) হতে পাই, x – 1 = y – 2

বা, x = y – 2 + 1

∴ x = y – 1 . . . . .. . (iii)

সমীকরণ (ii)-এ x এর মান বসিয়ে পাই,

y + 2 = 2(y – 1) + 1

বা, y + 2 = 2y – 2 + 1

বা, y – 2y =–2 + 1 – 2

বা, – y = –3

∴ y = 3

এখন, সমীকরণ (iii) এ y এর মান বসিয়ে পাই,

x = 3 – 1

∴ x = 2

নির্ণেয় মান x = 2, y = 3

(খ) (ax – cy, a² – c²) = (0, ay – cx) হলে,, (x, y) এর মান নির্ণয় কর।

সমাধান : দেওয়া আছে, (ax – cy, a² – c²) = (0, ay – cx)

ক্রমজোড়ের সংজ্ঞানুসারে, ax –cy = 0 . . . . . . . (i)

এবং a² –c² = ay – cx

∴ – cx + ay = a² – c² . . . . . .(ii)

সমীকরণ (i) হতে পাই, ax – cy = 0

বা, ax = cy

∴ x = $frac{{cy}}{a}$ . . . . . . .(iii)

সমীকরণ (ii) এ x এর মান বসিয়ে পাই,

$- {rm{ c }}frac{{cy}}{a}$ + ay = a² – c²

বা , $frac{{ - c2y + a2y}}{a}$ = a² – c²

বা, ${rm{ }}frac{{y(a2 - c2)}}{a}$ = a² – c²

বা, y(a²– c²) = a(a² –c²)

∴ y = a [উভয় পক্ষকে (a² – c²) দ্বারা ভাগ করে]

এখন, সমীকরণ (iii) এ y এর মান বসিয়ে পাই,

${rm{x = }}frac{{c.a}}{a}{rm{ }}therefore {rm{ x = c}}$

নির্ণেয় মান (x, y) = (c, a)

(গ) (6x – y, 13) = (1, 3x + 2y) হলে, (x, y) নির্ণয় কর।

সমাধান : দেওয়া আছে, (6x – y, 13) = (1, 3x + 2y)

ক্রমজোড়ের সংজ্ঞানুসারে, 6x – y = 1 . . . . (i)

এবং 13 = 3x + 2y

∴ 3x + 2y = 13 . . . . (ii)

সমীকরণ (i) কে ২ দ্বারা গুণ করে (ii) নং সমীকরণের সাথে যোগ করি,

12x –2y = 2

3x + 2y = 13

(+যোগ) 15x = 15

∴ x = 1

সমীকরণ (ii) এ x এর মান বসিয়ে পাই, 3× 1 + 2y = 13

বা, 3 + 2y = 13

বা, 2y = 13 – 3

বা, 2y = 10

বা, y = $frac{{10}}{2}$ ∴ y = 5

নির্ণেয় মান (x, y) = (1, 5)

$ads={1}

প্রশ্ন ৮ (ক) P = {a}, Q = {b, c} হলে, P × Q এবং Q × P নির্ণয় কর।

সমাধান : দেওয়া আছে, P = {a} এবং Q = {b, c}

∴ P × Q = {a} × {b, c} = {(a, b), (a, c)} (Ans.)

এবং Q × P = {b, c} × {a} = {(b, a), (c, a)} (Ans.)

(খ) A = {3, 4, 5}, B = {4, 5, 6} এবং C = {x, y} হলে, (A Ç B) × C নির্ণয় কর।

সমাধান : দেওয়া আছে, A = {3, 4, 5}, B = {4, 5, 6} এবং C = {x, y}

এখানে,A ∩ B = {3, 4, 5} ∩ {4, 5, 6} = {4, 5}

∴ (A ∩ B) × C = {4, 5} × {x, y}

= {(4, x), (4, y), (5, x), (5, y)}

∴ (A ∩ B) × C = {(4, x), (4, y), (5, x), (5, y)} (Ans.)

(গ) P = {3, 5, 7}, Q = {5, 7} এবং R = PQ হলে, (P ∪ Q) × R নির্ণয় কর।

সমাধান : দেওয়া আছে, P = {3, 5, 7}, Q = {5, 7}

∴ R = PQ = {3, 5, 7} {5, 7} = {3}

এখানে, P ∪ Q = {3, 5, 7} ∪ {5, 7} = {3, 5, 7}

∴ (P ∪ Q) × R = {3, 5, 7} ´ {3} = {(3, 3), (5, 3), (7, 3)}

∴ (P ∪ Q) × R = {(3, 3), (5, 3), (7, 3)} (Ans.)

প্রশ্ন ৯ A ও B যথাক্রমে 35 এবং 45 এর সকল গুণনীয়কের সেট হলে, A ∪ B এবং A ∩ B নির্ণয় কর।

সমাধান : এখানে, 35 = 1 ×35 = 5 ´ 7

35 এর গুণনীয়কগুলো হলো 1, 5, 7, 35

∴ A = {1, 5, 7, 35}

এবং 45 = 1 × 45

= 3 × 15

= 5 × 9

45 এর গুণনীয়কগুলো হলো, 1, 3, 5, 9, 15, 45

∴ B = {1, 3, 5, 9, 15, 45}

∴ A ∪ B = {1, 5, 7, 35} ∪ {1, 3, 5, 9, 15, 45}

= {1, 3, 5, 7, 9, 15, 35, 45} (Ans.)

এবং A ∩ B = {1, 5, 7, 35} ∩ {1, 3, 5, 9, 15, 45}

= {1, 5}(Ans.)

প্রশ্ন ১০ যে সকল স্বাভাবিক সংখ্যা দ্বারা 346 এবং 556 কে ভাগ করলে প্রতিক্ষেত্রে 31 অবশিষ্ট থাকে, এদের সেট নির্ণয় কর।

সমাধান : যে স্বাভাবিক সংখ্যা দ্বারা 346 এবং 556 কে ভাগ করলে প্রতিক্ষেত্রে 31 অবশিষ্ট থাকে, সে সংখ্যা হবে 31 অপেক্ষা বড় এবং 346 –31 = 315 এবং 556- 31 = 525 এর সাধারণ গুণনীয়ক।

মনে করি, 31 অপেক্ষা বড় 315 এর গুণনীয়কের সেট A

এবং 525এর গুণনীয়কের সেট B

এখানে, 315 = 1 × 315 = 3 × 105 = 5 × 63 = 7 × 45 = 9 × 35

= 15 × 21

31অপেক্ষা বড় 315এর গুণনীয়কগুলো হলো যথাক্রমে 35, 45, 63, 105 ও 315

∴ A = {35, 45, 63, 105, 315}

আবার, 525 = 1 × 525 = 3 × 175 = 5 × 105 = 7 × 75 = 15 × 35

= 21 × 25

31অপেক্ষা বড় 525 এর গুণনীয়কগুলো হলো যথাক্রমে 35, 75, 105, 175 ও 525

∴ B = {35, 75, 105, 175, 525}

∴ A ∩ B = {35, 45, 63, 105, 315} ∩ {35, 75, 105, 175, 525}

= {35, 105}

নির্ণেয় সেট {35, 105}

$ads={1}

প্রশ্ন ১১ কোনো শ্রেণির 30 জন শিক্ষার্থীর মধ্যে 20 জন ফুটবল এবং 15 জন ক্রিকেট খেলা পছন্দ করে। দুইটি খেলাই পছন্দ করে তদ্রুপ শিক্ষার্থীর সংখ্যা 10; কতজন শিক্ষার্থী দুইটি খেলাই পছন্দ করে না তা ভেনচিত্রের সাহায্যে নির্ণয় কর।

সমাধান : নিচের আয়তাকার ভেনচিত্রটি 30 জন শিক্ষার্থীর সেট S নির্দেশ করে F ও C দ্বারা নির্দেশিত বৃত্তাকার ক্ষেত্র দুইটি যথাক্রমে ফুটবল এবং ক্রিকেট খেলা পছন্দ করে এমন শিক্ষার্থীর সেট নির্দেশ করে। ভেনচিত্রটি চারটি নির্দিষ্ট সেটে বিভক্ত হয়েছে, যাদের P₁, P₂, P₃ ও P₄ দ্বারা বিভক্ত করা হলো।

এখানে, P₂ = F ∩ C =দুইটি খেলাই পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 10

P₁ = F P₂ =শুধু ফুটবল খেলা পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 20-10 = 10

P₃ = C P₂ =শুধু ক্রিকেট খেলা পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 15 – 10 = 5

∴ F ∪ C = P₁ ∪ P₂ ∪ P₃ = এক এবং উভয় খেলা পছন্দ শিক্ষার্থীদের সেট এবং সদস্য সংখ্যা = 10 + 10 + 5 = 25

∴ P₄ = S(F ∪ C) = দুইটি খেলাই পছন্দ করে না শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 30 -25 = 5

নির্ণেয় 5 জন শিক্ষার্থী দুইটি খেলাই পছন্দ করে না।

প্রশ্ন ১২ 100 জন শিক্ষার্থীর মধ্যে কোনো পরীক্ষায় 65% শিক্ষার্থী বাংলায়, 48% শিক্ষার্থী বাংলা ও ইংরেজি উভয় বিষয়ে পাস এবং 15% শিক্ষার্থী উভয় বিষয়ে ফেল করেছে।

ক. সংক্ষিপ্ত বিবরণসহ ওপরের তথ্যগুলো ভেনচিত্রে প্রকাশ কর।

খ. শুধু বাংলায় ও ইংরেজিতে পাস করেছে তাদের সংখ্যা নির্ণয় কর।

গ. উভয় বিষয়ে পাস এবং উভয় বিষয়ে ফেল সংখ্যাদ্বয়ের মৌলিক গুণনীয়কসমূহের সেট দুইটির সংযোগ সেট নির্ণয় কর।

সমাধান :

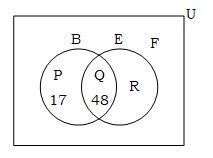
(ক) ভেনচিত্রে আয়তাকার ক্ষেত্রটি 100 জন পরীক্ষার্থীর সেট U এবং পরস্পরচ্ছেদী দুইটি বৃত্তক্ষেত্র দ্বারা বাংলা ও ইংরেজিতে পাস পরীক্ষার্থীদের সেট যথাক্রমে B ও E নির্দেশ করা হলো।